1, Tree definition

In computer science, tree (English: tree) is an abstract data type (ADT) or a data structure that implements this abstract data type, which is used to simulate a data set with the nature of tree structure. It is a set with hierarchical relationship composed of n (n > 0) finite nodes. It is called "tree" because it looks like an upside down tree, that is, it has roots up and leaves down.

This is an academic definition. In a simple vernacular, a tree can be regarded as a bunch of grapes.

2, Tree species

The following lists some trees that are often contacted during development, and briefly classifies them as follows:

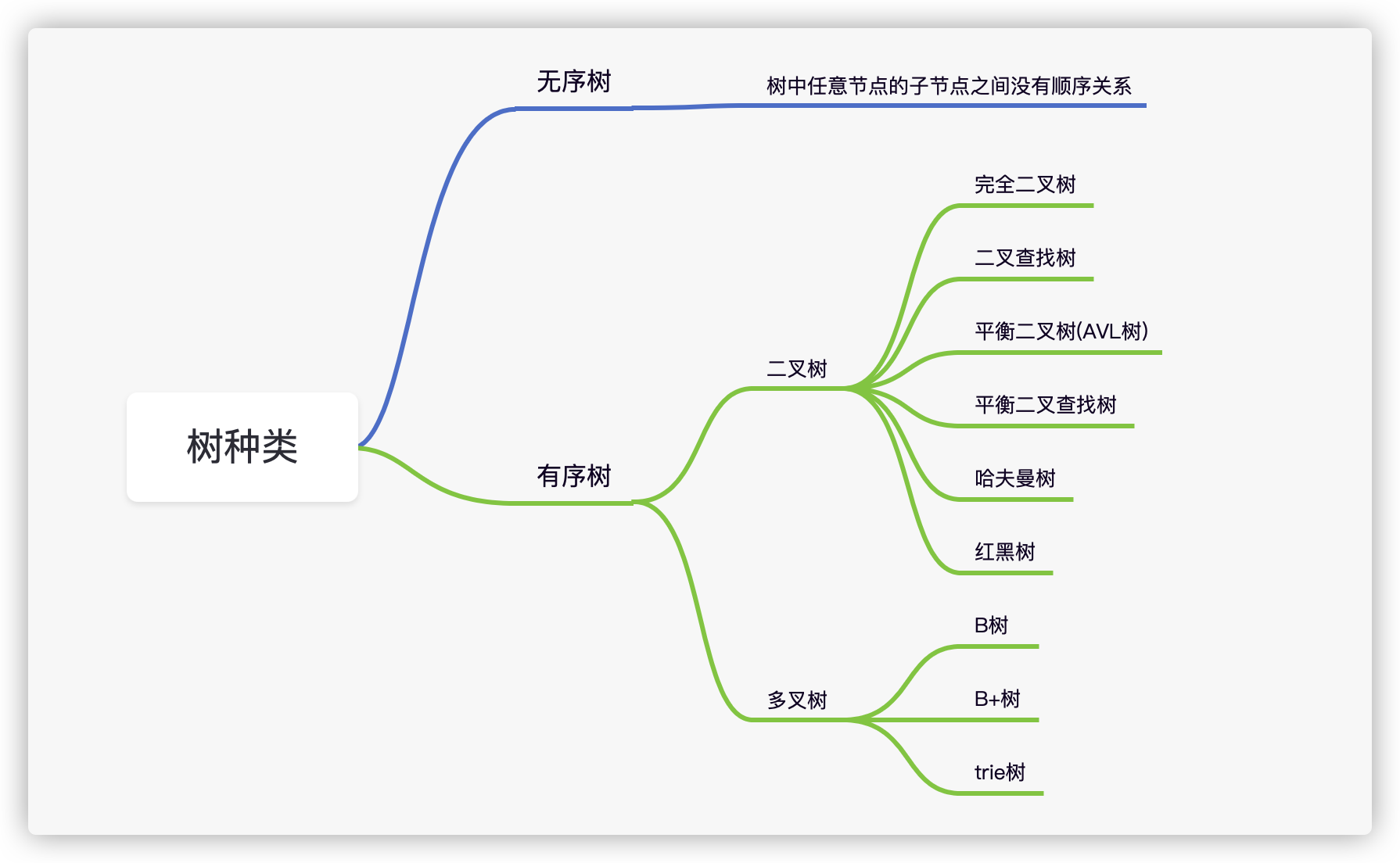
3, Common terms

term	meaning
Degree of node	The number of subtrees contained in a node is called the degree of the node
Degree of tree	In a tree, the largest node degree is called the degree of the tree
Leaf node	Node with zero degree
Branch node	Node with non-zero degree
Parent node	If a node has children, it is called parent of the its children
Child node	The root node of the subtree contained in a node is called the child node of the node
Sibling node	Nodes with the same parent node are called siblings
arrangement	Starting from the definition of the root, the root is the first layer, and the child node of the root is the second layer
depth	For any node n, the depth of n is the length of the unique path from the root to N, and the depth of the root is 0
height	For any node n, the height of n is the longest path from n to a leaf, and the height of all leaves is 0
forest	The collection of m (m > = 0) disjoint trees is called forest

4, Binary tree definition

A binary tree has at most two subtrees per node (that is, there are no nodes with a degree greater than 2 in the binary tree), and the subtrees of the binary tree can be divided into left and right, and their order can not be reversed arbitrarily.

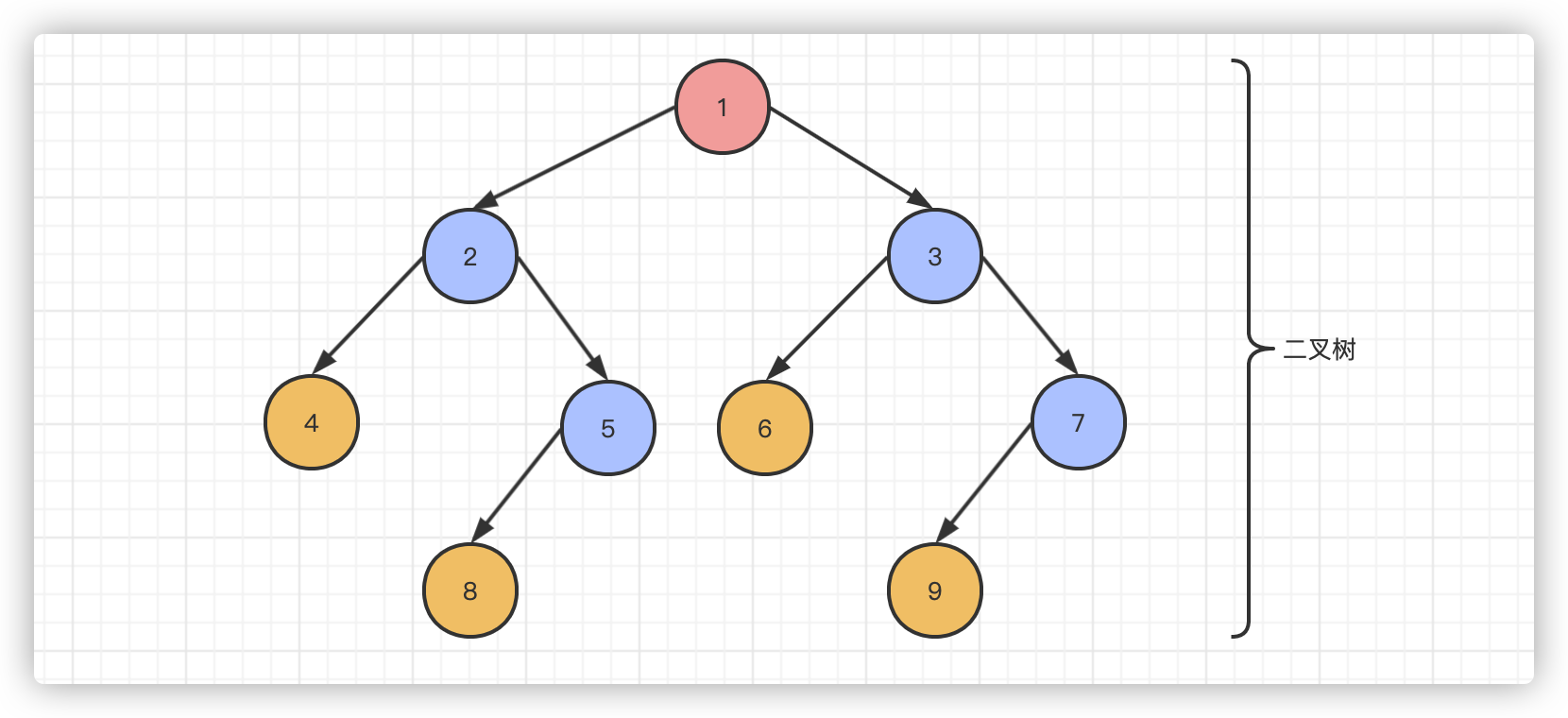
5, Properties of binary tree

There are several common properties:

• There are at most $2^{n-1} $nodes (n ≥ 1) on the nth component of the binary tree

• A binary tree with depth k has at most 2 k − 1 2^k-1 2k − 1 node (k ≥ 1)

• For any binary tree T, if the number of terminal nodes is a and the node tree with degree 2 is b, then a=b+1

• The depth of a complete binary tree with n nodes is l o g 2 n + 1 log_2n+1 log2​n+1

6, Implementation of binary tree

Here, we use golang as the programming language to implement binary tree. The principle is the same, and it can also be implemented in other languages. Here are several important methods about binary tree:

• Traversing a binary tree (recursive / non recursive): before, during, after, and hierarchy

• Depth of binary tree

6.1. Define binary tree

Define the basic operation interface first

type BinaryTreeOperation interface {
  RecursionPreOrderTraverse()  //   Recursive preorder traversal
  PreOrderTraverse()           //   Non recursive preorder traversal
  RecursionInOrderTraverse()   //   Recursive middle order traversal
  InOrderTraverse()            //   Non recursive middle order traversal
  RecursionPostOrderTraverse() //   Recursive postorder traversal
  PostOrderTraverse()          //   Non recursive postorder traversal
  LevelTraverse()              // level traversal 

  TreeDepth() int   // Tree depth
  CountLeaves() int // Number of leaves
  CountNodes() int  // Node number
}

Then the node and operation implementation class of binary tree are defined

// TreeNode binary tree node definition
type TreeNode struct {
  data int
  Left *TreeNode
  Right *TreeNode
}

// NewTreeNode builds node data
func NewTreeNode(left, right *TreeNode, data int) *TreeNode {
  return &TreeNode{Left: left, Right: right, data: data}
}

// BinaryTree binary tree implementation
type BinaryTree struct {
  root *TreeNode
}

Initialization data. The data constructed here is the binary tree in the definition of binary tree in part 4

// Constructor for NewBinaryTree binary tree
func NewBinaryTree() *BinaryTree {
  tree := &BinaryTree{}
  tree.InitTree()
  return tree
}

// InitTree initializes binary tree data
func (b *BinaryTree) InitTree() {
  node9 := NewTreeNode(nil, nil, 9)
  node8 := NewTreeNode(nil, nil, 8)
  node7 := NewTreeNode(node9, nil, 7)
  node6 := NewTreeNode(nil, nil, 6)
  node5 := NewTreeNode(node8, nil, 5)
  node4 := NewTreeNode(nil, nil, 4)
  node3 := NewTreeNode(node6, node7, 3)
  node2 := NewTreeNode(node4, node5, 2)
  b.root = NewTreeNode(node2, node3, 1)
}

The preparatory work has been completed. Now we begin to realize the related operations of binary tree!

6.2. Recursive traversal

Here, the anonymous function of golang is used to modify the shared variables to realize recursive traversal.

6.2.1. Preorder traversal

Traversal principle: if binary tree is empty, this operation is empty; Otherwise, access the root node, left subtree and right subtree.

func (b *BinaryTree) RecursionPreOrderTraverse() {
  // Store traversal data
  result := make([]int, 0)
  // Define anonymous functions
  var innerTraverse func(node *TreeNode)
  
  // Anonymous function implementation
  innerTraverse = func(node *TreeNode) {
    // Preorder traversal is root, left and right
    result = append(result, node.data)
    if node.Left != nil {
      innerTraverse(node.Left)
    }
    if node.Right != nil {
      innerTraverse(node.Right)
    }
  }
  // The current binary tree is not empty. Call the internal anonymous function
  if b.root != nil {
    innerTraverse(b.root)
  }
  // Output results
  fmt.Printf("Preorder traversal:%v\n", result)
}

6.2.2. Middle order traversal

Traversal principle: if binary tree is empty, this operation is empty; Otherwise, access the left subtree, root node and right subtree.

This is basically the same as the preorder traversal, but the position of append is different.

func (b BinaryTree) RecursionInOrderTraverse() {
  result := make([]int, 0)

  var innerTraverse func(node *TreeNode)

  innerTraverse = func(node *TreeNode) {
    if node.Left != nil {
      innerTraverse(node.Left)
    }
    result = append(result, node.data)
    if node.Right != nil {
      innerTraverse(node.Right)
    }
  }
  if b.root != nil {
    innerTraverse(b.root)
  }

  fmt.Printf("Middle order traversal:%v\n", result)
}

6.2.3. Post order traversal

Traversal principle: if binary tree is empty, this operation is empty; Otherwise, access the left subtree, right subtree and root node.

func (b BinaryTree) RecursionPostOrderTraverse() {
  result := make([]int, 0)

  var innerTraverse func(node *TreeNode)

  innerTraverse = func(node *TreeNode) {
    if node.Left != nil {
      innerTraverse(node.Left)
    }
    if node.Right != nil {
      innerTraverse(node.Right)
    }
    result = append(result, node.data)
  }
  if b.root != nil {
    innerTraverse(b.root)
  }

  fmt.Printf("Post order traversal:%v\n", result)
}

6.3. Non recursive traversal

6.3.1. Preorder traversal

Execution diagram: the execution process of pre, middle and post sequence traversal is the same, and the difference lies in the sequence of obtaining data.

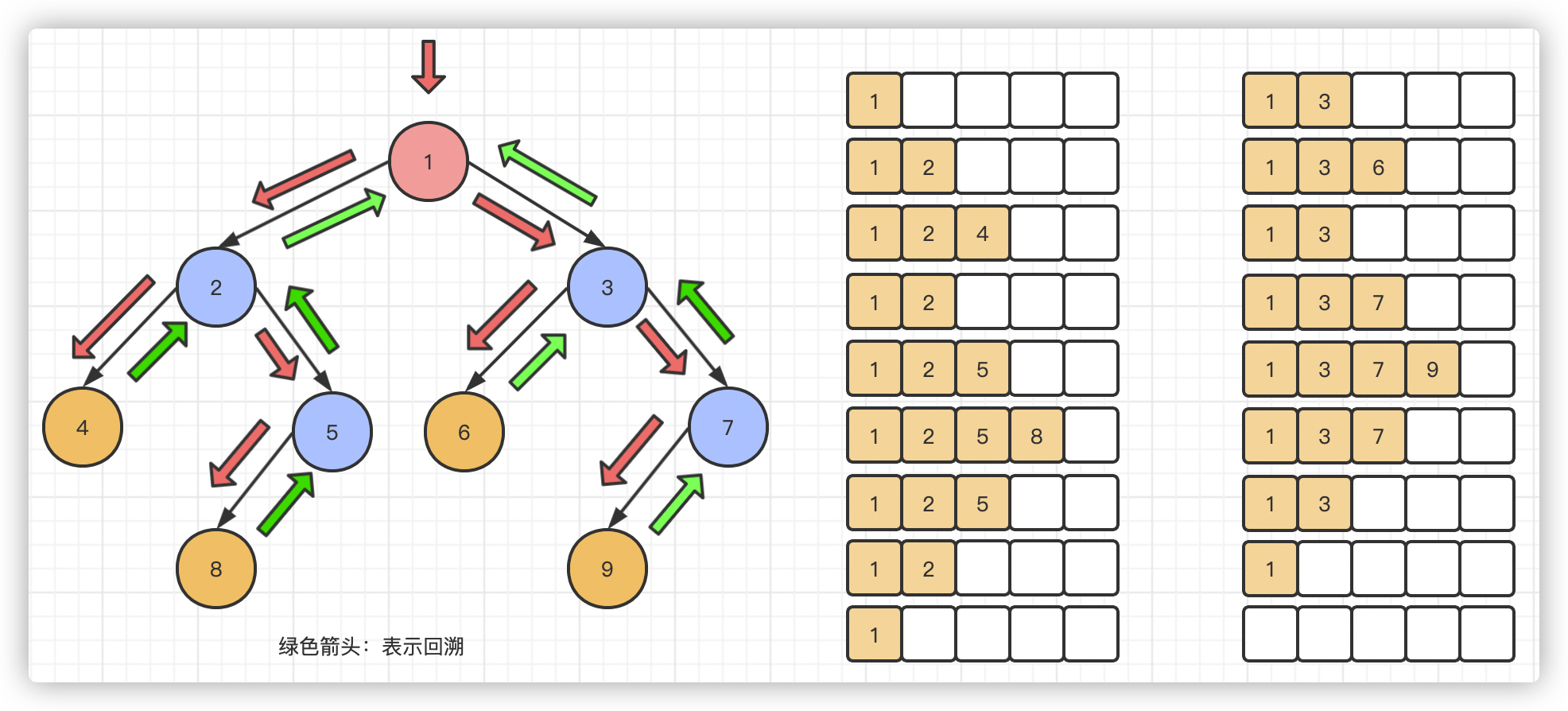
Execution Description: This is equivalent to putting the recursive execution process on the desktop (recursion is equivalent to putting the executed function call into a function call stack). Out of the stack into the stack is equivalent to function call.

// PreOrderTraverse non recursive preorder traversal
func (b BinaryTree) PreOrderTraverse() {
  // Simulation stack
  stack := make([]*TreeNode, 0)
  // Store traversal data
  result := make([]int, 0)
  // Judge whether the binary tree is empty
  if b.root == nil {
    return
  }
  // Point the pointer to the root node
  start := b.root
  
  for start != nil || len(stack) != 0 {
    // First traverse the left subtree until the left subtree is nil
    if start != nil {
      // Each traversal puts the node data into the cache array
      result = append(result, start.data)
      // Save the current node to the simulated stack
      stack = append(stack, start)
      // Point the current pointer to the left subtree of the next node
      start = start.Left
    } else {
      // When the node of the pointer is nil, it indicates that the current pointer has pointed to the leaf node of the left subtree
      
      lens := len(stack) - 1
      // Get the node element at the top of the stack
      pop := stack[lens]
      // Simulated out of stack
      stack = stack[:lens]
      // The pointer points to the right subtree of the node
      start = pop.Right
    }
  }
  
  fmt.Printf("Non recursive preorder traversal:%v\n", result)
}

Execution process:

• First, judge whether the current binary tree is an empty tree. If not, point the pointer to the root node;

• Judge whether the current pointer is empty and whether the current stack is empty;

• Then judge that the current pointer is not empty, put the node data pointed to by the previous pointer into the cache array, and put the current pointer on the stack;

• Until the current pointer is empty, it indicates that the leaf node of the left subtree has been reached. At this time, it is necessary to backtrack (assign the top element of the stack to the current pointer, and then push the stack out of the stack). Until the node pointed to by the current pointer is not nil, assign the right subtree address of the node pointed to by the current pointer to the current pointer.

• The following processes are similar in turn. When the elements in the stack are empty, it jumps out of the loop.

6.3.2. Middle order traversal

The middle order traversal needs to obtain data during backtracking.

func (b BinaryTree) InOrderTraverse() {
  // Simulation stack
  stack := make([]*TreeNode, 0)
  // Store traversal data
  result := make([]int, 0)
  // Judge whether the binary tree is empty
  if b.root == nil {
    return
  }

  start := b.root

  for start != nil || len(stack) != 0 {

    if start != nil {
      stack = append(stack, start)
      start = start.Left
    } else {
      lens := len(stack) - 1
      pop := stack[lens]
      result = append(result, pop.data)
      stack = stack[:lens]
      start = pop.Right
    }
  }
  fmt.Printf("Non recursive middle order traversal:%v\n", result)
}

6.3.3. Post order traversal

This subsequent traversal is troublesome. You need to ensure that the left and right child nodes are traversed before you can output the root node. Here, you need to add a delayed pointer to the element out of the stack.

func (b BinaryTree) PostOrderTraverse() {
  // Simulation stack
  stack := make([]*TreeNode, 0)
  // Store traversal data
  result := make([]int, 0)
  // Judge whether the binary tree is empty
  if b.root == nil {
    return
  }
  var temp *TreeNode

  stack = append(stack, b.root)

  for len(stack) != 0 {

    cur := stack[len(stack) - 1]
    // The current node is nil / the deferred pointer is not null, and the left or right pointer of the deferred pointer is the same as the current stack top pointer
    // This indicates that the left and right child nodes are traversed.
    if (cur.Left == nil && cur.Right == nil) || (temp != nil && (temp == cur.Left || temp == cur.Right)) {
      result = append(result, cur.data)
      temp = cur
      stack = stack[:len(stack) - 1]
    } else {
      // Ensure that the right node pointer is put into the stack first, so that the left node pointer can precede the right node pointer
      if cur.Right != nil {
        stack = append(stack, cur.Right)
      }
      if cur.Left != nil {
        stack = append(stack, cur.Left)
      }
    }

  }

  fmt.Printf("Non recursive postorder traversal:%v\n", result)
}

Sketch Map:

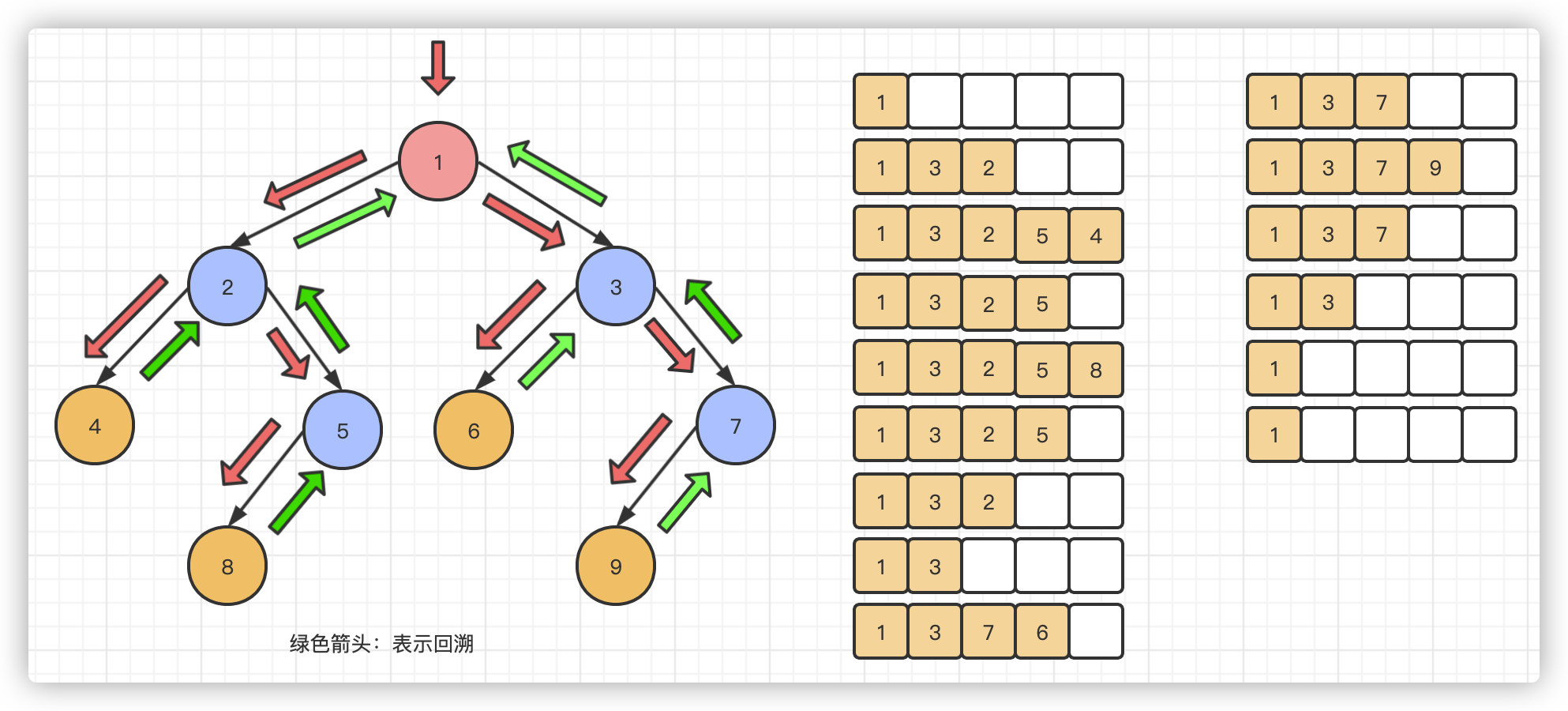
6.4. Level traversal

This level traversal also relies on queue first in first out.

// LevelTraverse hierarchy traversal
func (b BinaryTree) LevelTraverse() {
  // Store traversal data
  result := make([]int, 0)
  queue := make([]*TreeNode, 0)
  // Judge whether the binary tree is empty
  if b.root == nil {
    return
  }
  // Put the first element
  queue = append(queue, b.root)
  for len(queue) > 0 {
    // Gets the element of the queue header in the queue
    head := queue[0]
    // Let the team head out of the team
    queue = queue[1:]
    // Get header element
    result = append(result, head.data)
    // If the left subtree is not empty, join the end of the queue
    if head.Left != nil {
      queue = append(queue, head.Left)
    }
    // If the right subtree is not empty, it will be added to the end of the queue
    if head.Right != nil {
      queue = append(queue, head.Right)
    }
  }
  fmt.Printf("Hierarchy traversal:%v\n", result)
}

Sketch Map:

6.5. Maximum depth

Recursive implementation!

func (b BinaryTree) TreeDepth() int {
  if b.root == nil {
    return 0
  }
  var innerDepth func(node *TreeNode) int
  // Define anonymous functions
  innerDepth = func(node *TreeNode) int {

    if node == nil {
      return 0
    }

    l := innerDepth(node.Left) + 1
    r := innerDepth(node.Right) + 1

    if l < r {
      l, r = r, l
    }

    return l

  }
  return innerDepth(b.root)
}

Without recursion, you can also modify the level traversal to achieve the maximum depth acquisition.

7, Binary lookup tree

It can also be seen from the above that binary trees have no order and order. Search, insert and delete on the binary tree are not allowed. Therefore, the following describes the widely used binary search tree.

7.1. Properties of binary search tree

The properties of binary search tree are as follows:

• If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node;

• If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of its root node;

A typical binary search tree is shown in the figure below:

7.2. Create (add node)

Binary search tree is evolved from binary tree and can be extended based on the above binary number.

To build a binary lookup tree, we need to pay attention to meeting the properties of binary lookup tree.

In addition, it should be noted that for the processing of duplicate elements of binary search tree, the basic data type of int is used here. If this processing method is found to be the same, it will not be inserted; However, the data area may be a complex data type such as object. Here, we need to consider adding additional areas to store or store them in another tree (this case will not be discussed too much here).

To create a binary search tree, it is better to find nodes through traversal and then insert them. Therefore, with the basis of the above binary tree, we can implement it with a little modification in the traversal method.

func (b *BinaryTree) Insert(data int) {
  // If the root node is nil, it is created
  if b.root == nil {
    b.root = NewTreeNode(nil, nil, data)
    return
  }
  // Define anonymous recursive functions
  var innerTraverse func(node *TreeNode)
  
  innerTraverse = func(node *TreeNode) {
    // If the current node data is less than data, you need to find it on the right subtree
    if node.data < data {
      // If the right subtree is nil at this time, it can be assigned directly
      if node.Right == nil {
        node.Right = NewTreeNode(nil, nil, data)
      } else {
        // No, look down
        innerTraverse(node.Right)
      }

    } else {
      // Similar to the right subtree operation
      if node.Left == nil {
        node.Left = NewTreeNode(nil, nil, data)
      } else {
        innerTraverse(node.Left)
      }
    }
  }
  innerTraverse(b.root)
}

At this time, a binary search tree in 7.1 is constructed as follows:

tree := binary_tree.SimpleTree()

tree.Insert(10)
tree.Insert(7)
tree.Insert(15)
tree.Insert(9)
tree.Insert(8)
tree.Insert(18)
tree.Insert(12)
tree.Insert(3)
tree.Insert(13)

tree.RecursionInOrderTraverse()  // Middle order traversal: [3 7 8 9 10 12 13 15 18]

The middle order traversal here is to sort the output according to the size order!

7.3. Node data search

Given a data search, whether the binary lookup tree exists

func (b *BinaryTree) Search(data int) bool {
  
  // If the root node is nil, false is returned directly
  if b.root == nil {
    return false
  }

  var innerTraverse func(node *TreeNode) bool

  innerTraverse = func(node *TreeNode) bool {
    // The current node is nil and returns false
    if node == nil {
      return false
    } else {
      var status bool
      // equal
      if node.data == data {
        status = true
      } else if node.data < data {
        // Less than, continue to traverse the right subtree
        status = innerTraverse(node.Right)
      } else {
        // Greater than, continue to traverse the left subtree
        status = innerTraverse(node.Left)
      }
      return status
    }
  }
  
  // call
  return innerTraverse(b.root)
}

7.4. Obtain maximum and minimum values

The structure of binary search tree can be very simple until the leftmost node is the minimum and the rightmost node is the maximum.

func (b *BinaryTree) MaxValue() (int, error) {
  if b.root == nil {
    return 0, errors.New("The current tree is empty")
  }

  p := b.root

  for p.Right != nil {
    p = p.Right
  }
  return p.data, nil
}

7.5. Delete the maximum and minimum nodes

Here is a method to delete the lowest node:

// DeleteMin deletes the smallest node in the binary lookup tree
func (b *BinaryTree) DeleteMin() bool {
  return b.deleteMin(b.root)
}

// DeleteMin deletes the smallest node under a node
func (b *BinaryTree) deleteMin(node *TreeNode) bool {
  if node == nil {
    return false
  }
  // Pointer used to save the parent node
  var prev *TreeNode
  // Traverse to find the smallest node
  for node.Left != nil {
    prev = node
    node = node.Left
  }
  // If the left node is not nil, the left child pointer of the parent node of the node to be deleted points to the right child of the node to be deleted
  if node.Right != nil {
    prev.Left = node.Right
  } else {
    // Otherwise, the left child pointer of the parent node of the node to be deleted directly points to nil
    prev.Left = nil
  }
  return true
}

First deletion:

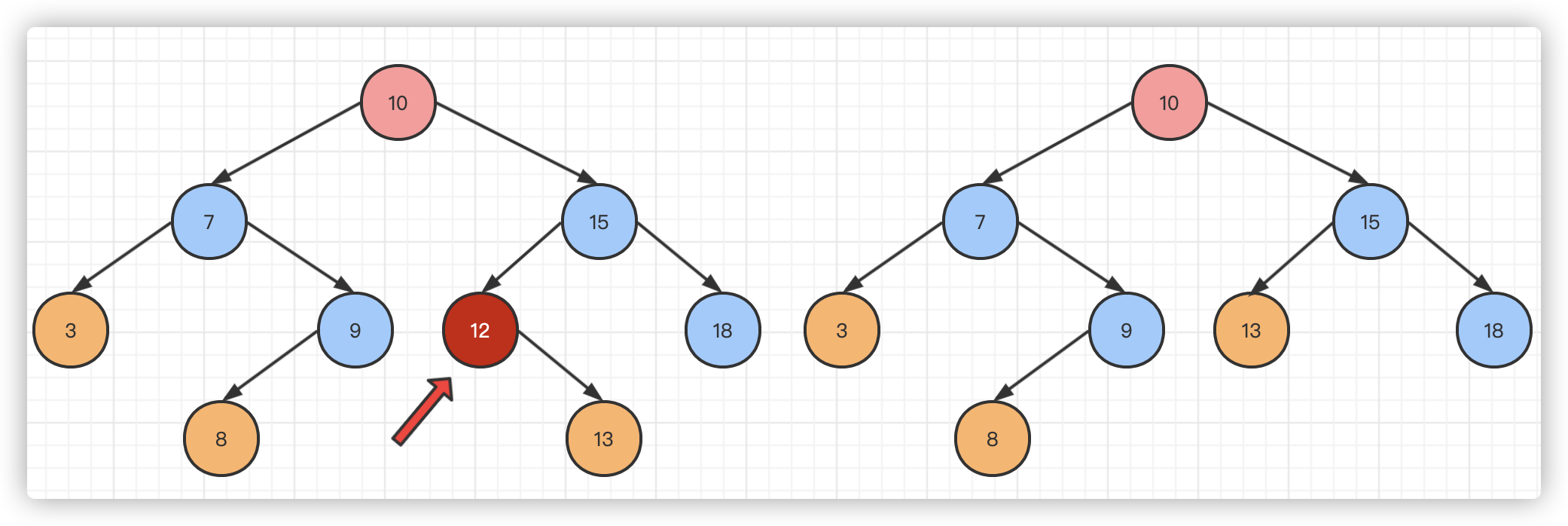
The second deletion:

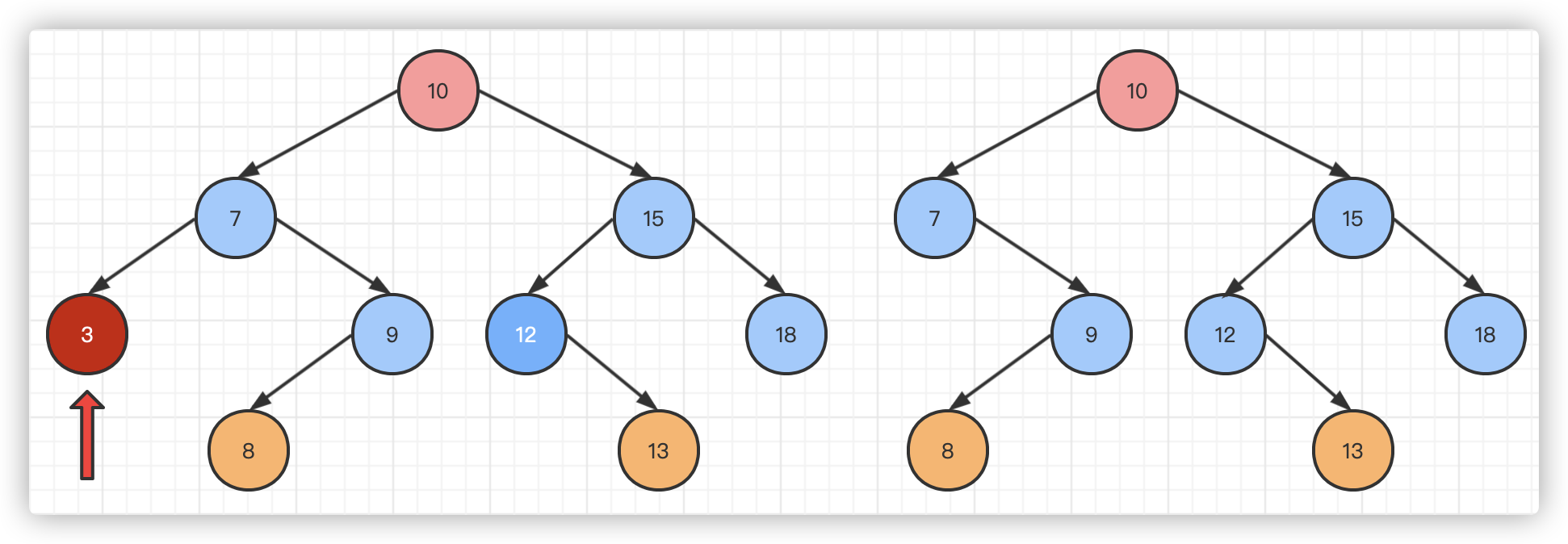
7.5. Delete node

The operation here is troublesome and involves four situations, which are described one by one below:

The first case: the deleted node does not exist: in this case, you can delete the node directly

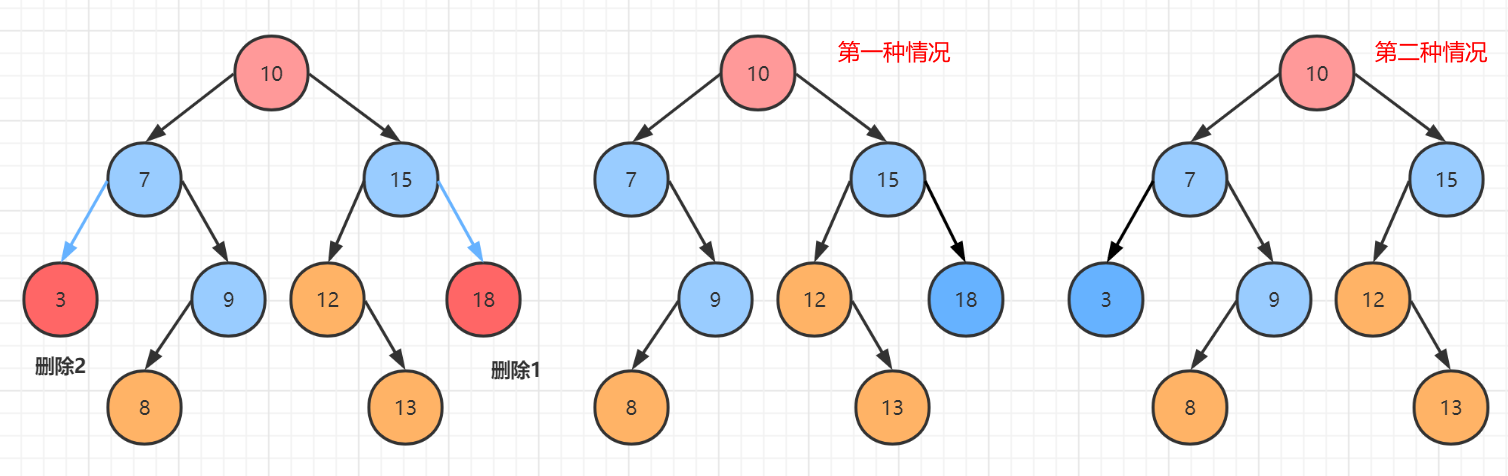
The second case: the deleted node has a left child: at this time, directly let the parent node of the node point to the left child of the current node, and then delete the current node;

The third case: the deleted node has a right child: at this time, directly let the parent node of the node point to the left child of the current node, and then delete the current node;

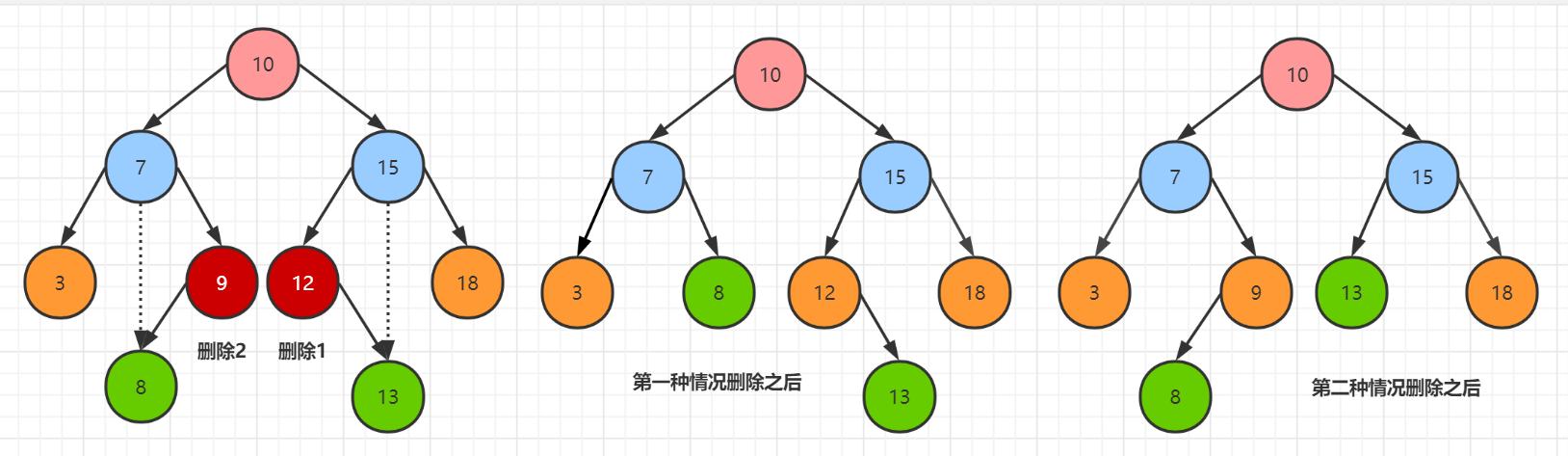
The fourth case: the deleted node has left and right children: find the right subtree, find the smallest node, exchange the value with the current node, and finally delete it

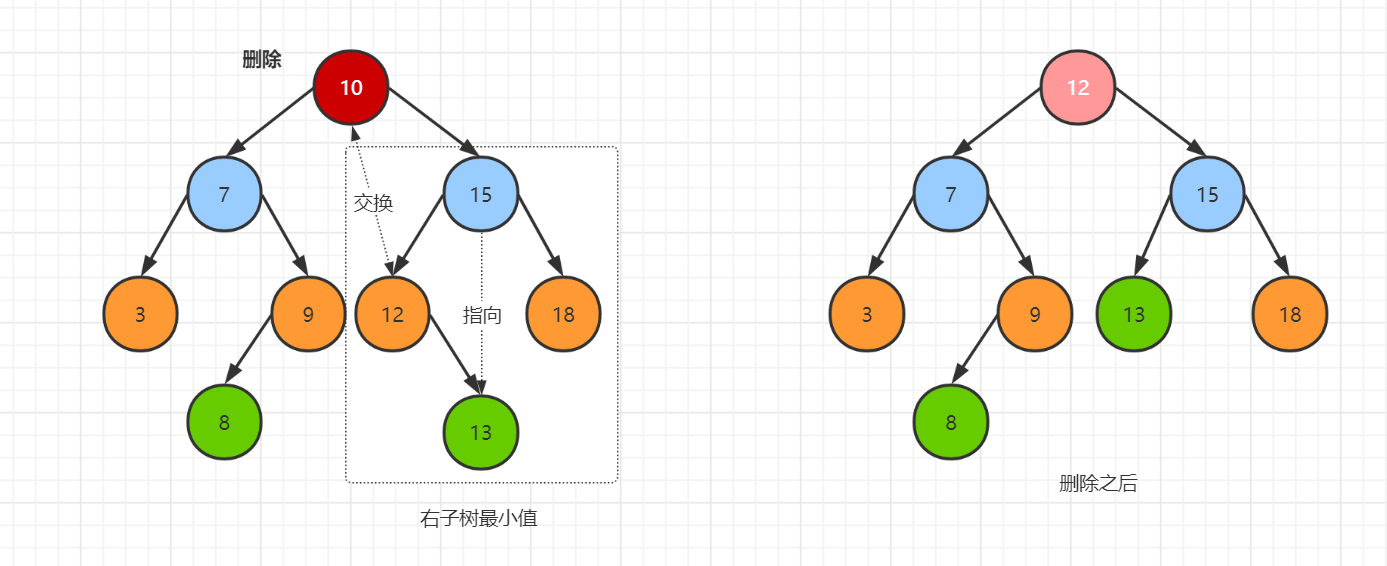
Code implementation:

func (b *BinaryTree) min(node *TreeNode) (int, error) {
  if node == nil {
    return 0, errors.New("Node is empty")
  }
  for node.Left != nil {
    node = node.Left
  }
  return node.data, nil
}

// DeleteMin deletes the smallest node under a node
func (b *BinaryTree) deleteMin(node *TreeNode) (bool, error) {
  if node == nil {
    return false, errors.New("Current node is nil")
  }

  if node.Left == nil && node.Right == nil {
    return false, errors.New("The current node does not have child nodes")
  }
  var prev *TreeNode

  for node.Left != nil {
    prev = node
    node = node.Left
  }
  if node.Right != nil {
    prev.Left = node.Right
  } else {
    prev.Left = nil
  }
  return true, nil
}

// DeleteNode delete node
func (b *BinaryTree) DeleteNode(data int) bool {

  var prev *TreeNode
  var status bool
  curr := b.root

  if curr == nil {
    return false
  }

  // First find the node location to delete
  for curr != nil {
    if curr.data < data {
      prev = curr
      curr = curr.Right
      continue
    } else if curr.data > data {
      prev = curr
      curr = curr.Left
      continue
    } else {
      status = true
      break
    }
  }

  // If not found, return false directly
  if !status {
    return false
  }

  // Then delete the node
  if curr.Left == nil && curr.Right == nil {
    // The first case: the left and right subtrees of the found node are nil
    // However, there are two types of relationships with parent nodes:
    //    The first is: the left child pointer of the parent node points to the node to be deleted;
    //    The second method: the right child pointer of the parent node points to the node to be deleted;
    if prev.Right.data == curr.data {
      prev.Right = nil
    }
    if prev.Left.data == curr.data {
      prev.Left = nil
    }

  } else if curr.Left != nil && curr.Right == nil {
    // The second case: the left subtree of the found node is not empty, and the right subtree is nil
    // As in the first case, the combination of deleting a node and its parent node will also exist in two cases
    //    The first is: the left child pointer of the parent node points to the node to be deleted. You need to point the right subtree pointer of the parent node to the left subtree pointed to by the current node
    //    The second is: the right child pointer of the parent node points to the node to be deleted. You need to point the left subtree pointer of the parent node to the right subtree pointed to by the current node
    if prev.Right.data == curr.data {
      prev.Right = curr.Left
    }
    if prev.Left.data == curr.data {
      prev.Left = curr.Left
    }

  } else if curr.Left == nil && curr.Right != nil {
    // The third case: the right subtree of the node to be found is not empty, and the left subtree is nil, which is opposite to the second case
    if prev.Right.data == curr.data {
      prev.Right = curr.Right
    }
    if prev.Left.data == curr.data {
      prev.Left = curr.Right
    }
  } else {
    // The fourth case: the left and right subtrees are not empty
    // At this time, you need to find the smallest element in the right subtree and replace it with the content of the node to be deleted
    // Finally, delete the minimum node of the right subtree
    min, _ := b.min(curr.Right)
    curr.data = min
    if curr.Right.Left == nil && curr.Right.Right == nil {
      curr.Right = nil
    } else {
      b.deleteMin(curr.Right)
    }
  }
  return status
}

7.6. Note

Here, with the increase of nodes, stack overflow may occur when we use recursion. Non recursion is more recommended for the above operations.

Another problem is the degradation of binary search tree. Take an extreme example:

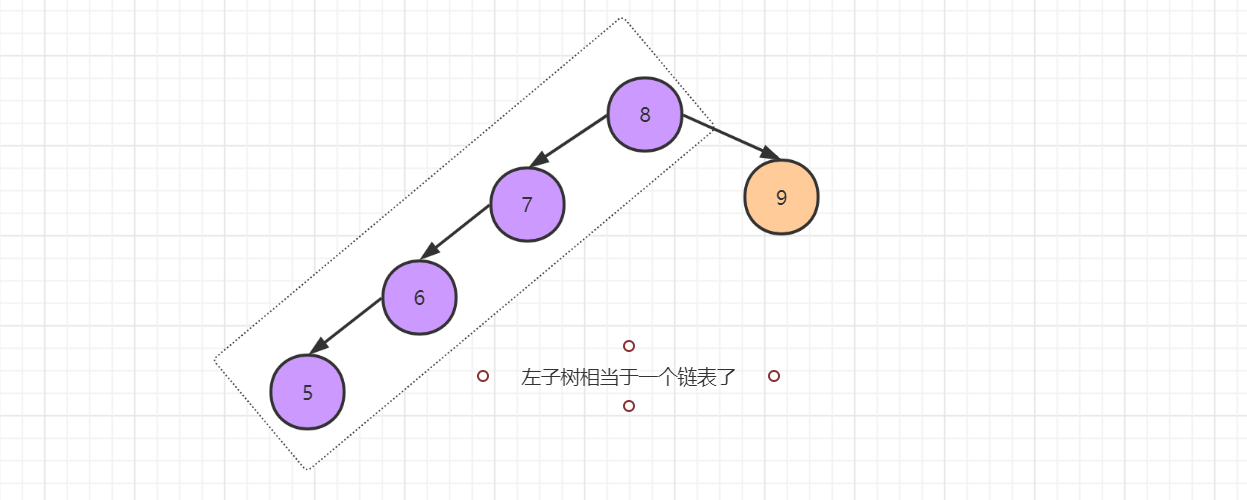
This situation also satisfies the condition of binary search tree. However, at this time, the binary search tree has approximately degenerated into a linked list. The search time complexity of such binary search tree immediately becomes O(n). It can be imagined that we must not let this happen. In order to solve this problem, we can use balanced binary tree (AVL).