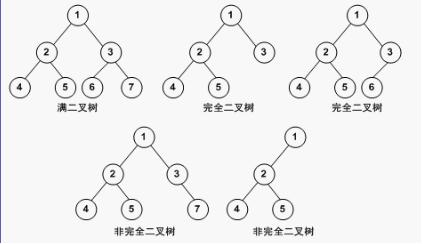
Terms of binary tree

Node: an element in a tree
Child node: the root of each subtree of a node
Parent node: the opposite concept of child node
Sibling node: a child node with the same parents
Ancestor node: both parent nodes from the root node to this node become ancestor nodes
Descendant node is the opposite concept of ancestor node
Degree of node: the number of subtrees of the node
Leaf node: a node whose degree is 0, also known as a terminal node
Branch node: a node whose degree is not 0, also known as a non terminal node
Number of layers: the node where the tree root is located is 1, and other nodes are parent nodes + 1
Number of layers: the maximum number of layers of tree node
Ordinal number and unordered number: each node of ordinal number

Properties of binary tree

Property 1: layer I of binary tree has at most 2i-1 nodes
Property 2: a binary tree with a depth of K has at most 2k-1 nodes
Property 3: in any binary tree, if the number of leaf nodes is n0, the number of nodes with degree 1 is n1, and the number of nodes with degree 2 is n2, then n2+1=n0.
Proof: n=n0+n1+n2
When there are n nodes, there are n-1 edges.
So n-1=0 x n0 + 1 x n1+ 2 x n2
Substituting equation 1 into equation 2 yields property 3.
Property 4: the depth of complete binary trees with n nodes is [log2 (n+1)]+1,[log2n] means to take the maximum integer not exceeding log2n.
It is proved that when there are n nodes, its value should be greater than the number of nodes of the full binary tree with depth k-1, and less than or equal to the number of nodes of the full binary tree with depth K.
Get the formula: 2k-1-1 < n < = 2k-1
Add one transformation 2k-1 < n + 1 < = 2K
Take the logarithm k-1 < log2 (n + 1) < = K
Since K is an integer, we can know that the maximum integer [log2(n+1)] for log2(n+1) does not exceed log2(n+1), and its value is k-1, so k=[log2(n+1)]+1. Example: 2 < 2.44 < 3, the maximum integer not exceeding 2.44 is 2.

Property 5: when a complete binary tree with n nodes is sequentially numbered, then for the node numbered i.
When i=1, the node is the root node and has no parents
When I > 1, the parent node of this node is [i/2]
When 2i < = n, there is a left child node, numbered 2i.
When 2i+1 < = n, there is a right child node numbered 2i+1

Traversal of binary tree

Node description

typedef struct node{
DataType data;
struct node * lch,*rch;// Pointer to left and right children respectively
}Bnode;

The algorithm is not a real code language, but only shows the logic, so it can't really run in the code. It can only make people understand the problem-solving steps. Therefore, sometimes what parameters suddenly appear without definition. Don't delve into it, just show the logic. In those years, I just had to fight it, so I was confused when learning data structure

recursive algorithm

1. Preorder traversal (root - left subtree - right subtree)

void firstorder(Bnode *p)  {
	printf("%6c",p->data);
	firstorder(p->lch);
	firstorder(p->rch);
}

2. Medium order traversal (left subtree root right subtree)

void middleorder(Bnode  *p) {
	firstorder(p->lch);
	printf("%6c",p->data);
	firstorder(p->rch);
}

3. Subsequent traversal (left subtree right subtree root)

void lastorder(* p) {
	firstorder(p->lch);
	firstorder(p->rch);
	printf("%6c",p->data);
}

Traverse by layer

The main idea is to join the binary tree in the team, take the team head element out of the team, and judge whether there are left and right children. If so, let them join the team, continue to repeat the team head element and judge... Until the team is empty.

void levelorder(Bnode  *p){
	Bnode *q[20];
	front=rear=0;//Head pointer tail pointer
	if(p!=null) {rear++;q[rear]=p;}//Root node is not empty, join the queue
	while(front!=rear){//Queue is not empty
		front++;p=q[front];//Out of line head element
			printf("%6c",p->data);
		if(p->lch!=null){rear++,q[rear]=p->lch;} //Left child joins the team
		if(p->rch!=null){rear++,q[rear]=p->rch;}//Right child joins the team
	}

}

non-recursive algorithm

Although the recursive algorithm is simple and convenient, its efficiency is relatively low, because the system needs to maintain a work stack to ensure the correctness of the recursive function. Therefore, the key of non recursive algorithm is that we need to artificially set the stack to imitate the working process of the system work stack.

1. Preorder traversal
Through the analysis of recursive preorder traversal, it can be concluded that each time the left subtree traversal of a node is completed, the node needs to be retrieved, and then the right subtree number needs to be traversed, so we need to store the passed node information in the stack.

void firstorder(Bnode *p){
top=-1; //Empty stack
while(p!=null||top!=-1){
  
  while(p!=null){
		printf("%6c",p->data);
	  top++;
	  s[top]=p->lch;
   }//while
   
   if(top!=-1){
	    p=s[top];
	    top--;
	    p=p->rch;
    }
}//while


}

2. Middle order traversal
The middle order traversal is output when it passes through this node for the second time, so the difference from the first order is the position of the output statement

void middleorder(Bnode *p){
top=-1; //Empty stack
while(p!=null||top!=-1){
  
  while(p!=null){
	  top++;
	  s[top]=p->lch;
   }//while
   
   if(top!=-1){
	    p=s[top];
	  	printf("%6c",p->data);
	    top--;
	    p=p->rch;
    }
}//while

}

3. Post order traversal
Post order traversal is more complex than pre order and middle order, because pre order and middle order are out of the stack and output when they pass through the second time. However, post order traversal requires three times before the node is output, indicating that it needs to pass through the third time before it is out of the stack. Therefore, an additional stack s2 should be added to describe how many times it passes through the node.

void lastorder(Bnode *p){
top=-1; //Empty stack
q=p;
bool=1;
while (bool) {

  while(q!=null){
  top++;
  s[top]=q->lch;
  s2[top]=1;
  }//while

if(top==-1 )  bool=0 ;//The stack is empty
else {
  if(s2[top]==1){//After the second pass, do not leave the team, find the right subtree
    s2[top]=2;
    q=s[top];
    q=q->rch; }
  else{ //The third pass, out of the team and output
    q=s[top];
    s2[top]=0;
    top--;
 	printf("%6c",p->data);
    q=null;
   }
}


}//while

}

Creation of binary tree

! [insert picture description here]( https://img-blog.csdnimg.cn/20210408134037402.png#pic_center

Recursive creation

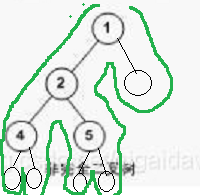
1. The idea of preorder recursive traversal is created
The algorithm traverses the generated binary tree in order. For example, you want to create a binary tree as shown in the figure above. For ease of understanding, I use o to represent the empty subtree to supplement the above figure. The order of values entered by the user should be the order of the first pass of the green line, 1,2,4,0,0,5,0,0,0. In this algorithm, a value of 0 represents a null subtree.

Bonde * creat(){
Bonde * p;
scanf(%d,&x);//Get value from user
if(x==0) p=null; //Represents that the subtree is an empty subtree
else {
	p=(Bnode *) malloc(sizeof(Bonde));//Get a node
	p->data=x;
	p->lch=creat();
	p->rch=creat();
 }
}

2. Create in the order of traversal
If the binary tree is generated by traversing in the middle order, the user will traverse the input in the first order, 1,2,4,0,0,5,0,0,0. However, when creating, the value is assigned in the order of 4251. Because the second pass is required, the valid value entered by the user is stored in a stack. When the second pass, the element at the top of the stack is assigned to the node, and then out of the stack.

int s[10];//Define a stack

Bonde * creat(int *s ,int top){
Bonde * p;
scanf(%d,&x);//Get the existence from the user
if(x==0) p=null; //Represents that the subtree is an empty subtree
else {
    top++;
    s[top]=x;//Store value in stack
	p=(Bnode *) malloc(sizeof(Bonde));//Get a node
	p->lch=creat(s,top)；
    p->data=s[top];
    top--;
	p->rch=creat(s,top);
 }
}

Create according to definition 5

According to the definition, when creating, it is the number to create the corresponding position, and connect the parent node with the node.

Bonde * creat(){
Bonde * t=null;
scanf("%d%d",&i,&x);//Get the location number and actual value from the user
while(i!=0&&x!=0){
	p=(Bnode *) malloc(sizeof(Bonde));//Get the space of a node
	p->data=x;
	p->lch=null;
	p->rch=null;
	s[i]=q;//The current node is stored
	if(i==1) t=i;  //Root node
	else {
		j=i/2;//Find the number of parent node
		if(i%2==0) s[j]->lcj=p; //It's a left child
		else s[j]->rch=p; //It's the right child
	}
	
}

}

Number depth of binary tree

Find the maximum depth of the left and right subtrees of the node, and take the maximum depth of the left and right subtrees plus 1.
Method of preorder traversal

int fstdepth(Bnode *p){
if(p==null) return 0;
else {
int dl=fstdepth(p->lch);
int dr=fstdepth(p->rch);
return 1+(dl>dr?dl:dr);
}
}