Binary tree (linked list implementation)
1.1 basic definition of tree
Tree is a very important data structure in our computer. At the same time, using this data structure can describe many things in real life, such as genealogy, organizational structure of units, and so on.
A tree is a set with hierarchical relations composed of n (n > = 1) finite nodes. It is called "tree" because it looks like an upside down tree, that is, it has roots up and leaves down.
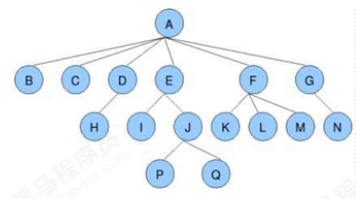
The tree has the following characteristics:
- Each node has zero or more child nodes;
- Nodes without parent nodes are root nodes;
- Each non root node has only one parent node;
- Each node and its descendants can be regarded as a tree as a whole, which is called a subtree of the parent node of the current node;
1.2 related terms of tree
Degree of node:
The number of subtrees contained in a node is called the degree of the node;
Leaf node:
A node with a degree of 0 is called a leaf node or a terminal node
Branch node:
A node whose degree is not 0 is called a branch node or a non terminal node
Node hierarchy:
Starting from the root node, the level of the root node is 1, the direct successor level of the root is 2, and so on
Sequence number of node:
The nodes in the tree are arranged into a linear sequence from the upper layer to the lower layer and from left to right in the same layer, and they are compiled into continuous natural numbers.
Degree of tree:
The maximum degree of all nodes in the tree
Height (depth) of the tree:
The maximum level of nodes in the tree
forest:
m (m > = 0) sets of disjoint trees, delete the root node of a non empty tree, and the tree becomes a forest; Add a unified root node to the forest, and the forest will become a tree
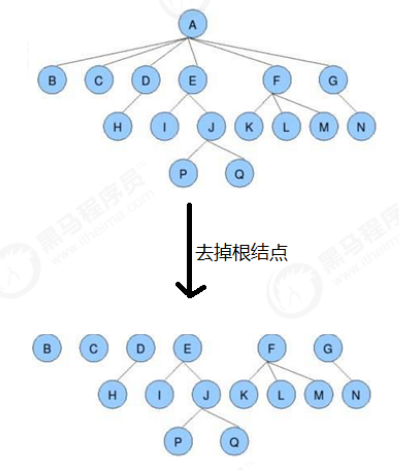
Child node:
The direct successor node of a node is called the child node of the node
Parent node (parent node):
The direct precursor of a node is called its parent node
Sibling node:
The child nodes of the same parent node are called brother nodes
1.3 basic definition of binary tree
A binary tree is a tree with a degree of no more than 2 (each node has at most two child nodes)
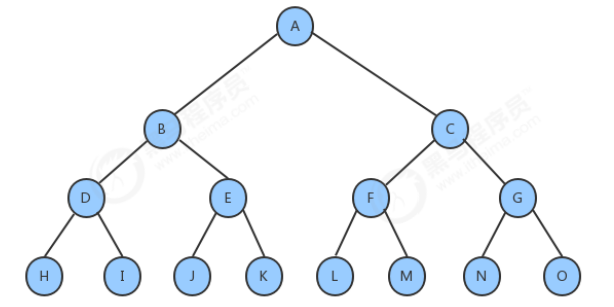
Full binary tree:
A binary tree is a full binary tree if the node tree of each layer reaches the maximum.
| describe | formula |
|---|---|
| Number of nodes in each layer | 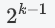 k is the number of layers k is the number of layers |
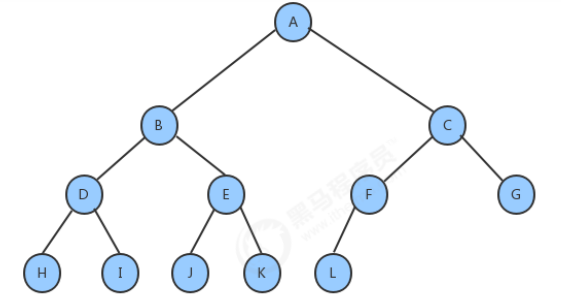
Complete binary tree:
Leaf nodes can only appear in the lowest and lower layers, and the nodes of the lowest layer are concentrated in several positions on the left of the layer
1.4 creation of binary search tree
Node API design:
| Class name | Node<Key,Value> |
|---|---|
| Construction method | Node (key, value, node left, node right): creates a node object |
| Member variable | 1.public Node left: records the left child node 2.public Node right: records the right child node 3. Public key: storage key 4. Public value: store value |
Binary lookup tree API design:
| Class name | BinaryTree<Key extends Comparable,Value> |
|---|---|
| Construction method | BinaryTree(): creates a BinaryTree object |
| Member variable | 1.private Node root: records the root node 2.private int N: number of elements in the record tree |
| Member method | 1. Public void put (key, value): inserts a key value pair into the tree 2. Private node put (node x, key, value, Val): add a key value pair to the specified tree X and return the added new tree 3. Public value get (key): find the corresponding value from the tree according to the key 4. Private value get (node x, key): find the value corresponding to the key from the specified tree X 5. Public void delete (key): deletes the corresponding key value pair in the tree according to the key 6. Private node delete (node x, key): deletes the key value pair whose key is key on the specified tree x, and returns the deleted new tree 7.public int size(): get the number of elements in the tree 8.public Key min(): find the smallest key in the tree 9.private Node min(Node x): find the node with the smallest key in the specified tree X 10.public Key max(): find the largest key in the tree 11.public Node max(Node x): find the node with the largest key in the specified tree X |
Implementation of binary search tree
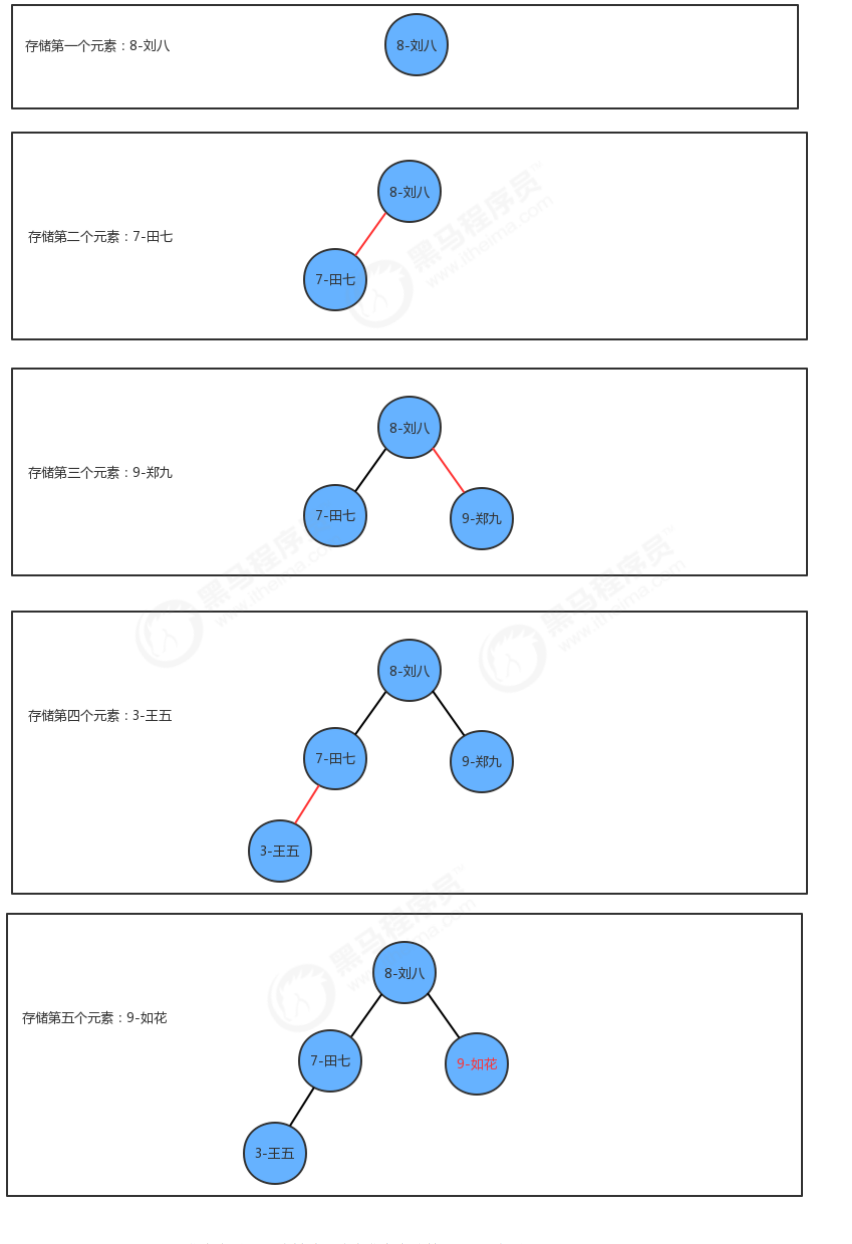
Implementation idea of insertion method:
1. If there is no node in the current tree, the new node is directly used as the root node
2. If the current tree is not empty, start from the root node:
2.1 if the key of the new node is less than the key of the current node, continue to find the left child node of the current node;
2.2 if the key of the new node is greater than the key of the current node, continue to find the right child node of the current node;
2.3 if the key of the new node is equal to the key of the current node, such a node already exists in the tree. Replace the value value of the node.
Implementation idea of query method get:
Start at the root node:
1. If the key to be queried is less than the key of the current node, continue to find the left child node of the current node;
2. If the key to be queried is greater than the key of the current node, continue to find the right child node of the current node;
3. If the key to be queried is equal to the key of the current node, the value of the current node will be returned in the tree.
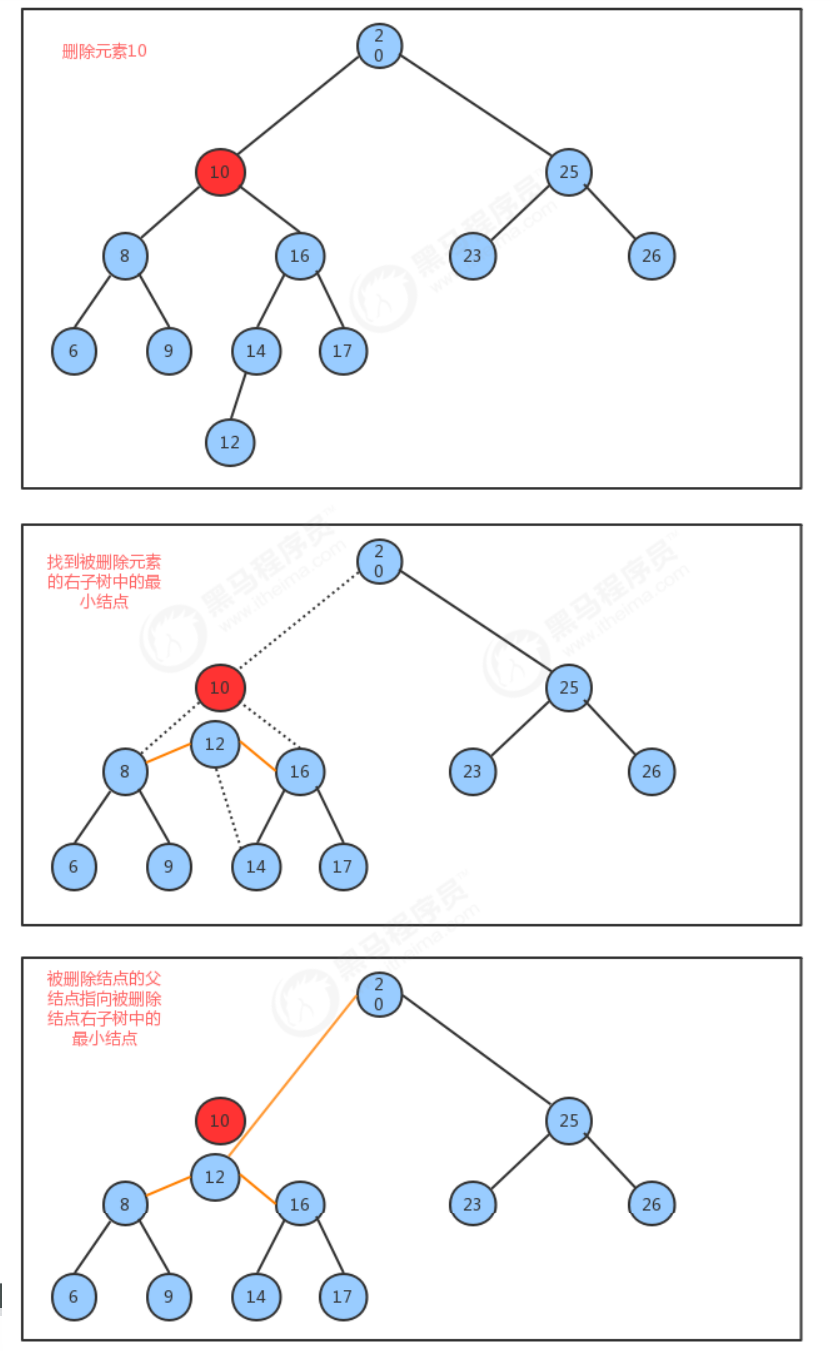
Implementation idea of delete method:
1. Find the deleted node;
2. Find the minimum node minNode in the right subtree of the deleted node
3. Delete the smallest node in the right subtree
4. Let the left subtree of the deleted node be called the left subtree of the minimum node minNode, and let the right subtree of the deleted node be called the right subtree of the minimum node minNode
5. Make the parent node of the deleted node point to the minimum node minNode
code:
/**
* Binary tree
*/
public class BinaryTree<Key extends Comparable<Key>, Value> {
// Record root node
private Node root;
// Record the number of elements in the tree
private int N;
public BinaryTree() {
}
// Gets the number of elements in the tree
public int size() {
return N;
}
// Add the element key value to the tree
public void put(Key key, Value value) {
root = put(root, key, value);
}
// Add key value to the specified tree x, and return the new tree after adding elements
private Node put(Node x, Key key, Value value) {
// If the x node is empty, a new node is directly created to store data and return
if (x == null) {
// Number of elements + 1
N++;
return new Node(key, value, null, null);
}
// If the X node is not empty, compare the x.key with the passed in key to find the insertion point
// If (key > x.key), continue to find the right child node of the current node
if (key.compareTo(x.key) > 0) {
x.right = put(x.right, key, value);
}
// If (key < x.key), continue to find the left child node of the current node
if (key.compareTo(x.key) < 0) {
x.left = put(x.left, key, value);
}
// If (key=x.key), replace the value value of the current node
if (key.compareTo(x.key) == 0) {
x.value = value;
}
return x;
}
// The value corresponding to the specified key in the query tree
public Value get(Key key) {
return get(root, key);
}
// From the specified tree x, find the value corresponding to the key
private Value get(Node x, Key key) {
// The x tree is null
if (x == null)
return null;
// x tree is not null
// If (key < x.key), recursively query the left subtree of the current node
if (key.compareTo(x.key) < 0) {
return get(x.left, key);
}
// If (key > x.key), recursively query the right subtree of the current node
if (key.compareTo(x.key) > 0) {
return get(x.right, key);
}
// If (key=x.key), return the value of the current node
if (key.compareTo(x.key) == 0) {
return x.value;
}
return null;
}
// Delete the value corresponding to the key in the tree
public void delete(Key key) {
delete(root, key);
}
// Delete the value corresponding to the key in the specified tree x, and return the deleted new tree
private Node delete(Node x, Key key) {
// If the x node is empty, it will be returned directly
if (x == null) {
return null;
}
// If the x node is not empty, compare the key value to find the node to be deleted
// If (key > x.key), find the right subtree of the current node
if (key.compareTo(x.key) > 0) {
x.right = delete(x.right, key);
}
// If (key < x.key), find the left subtree of the current node
if (key.compareTo(x.key) < 0) {
x.left = delete(x.left, key);
}
// If (key=x.key), find the node to delete and delete it
if (key.compareTo(x.key) == 0) {
// To find the smallest node in the right subtree of X node, replace x node
// If the right subtree of x node is empty, the left subtree of x is returned directly
if (x.right == null) {
// Number of elements - 1
N--;
return x.left;
}
// If the left subtree of x node is empty, the right subtree of x is returned directly
if (x.left == null) {
// Number of elements - 1
N--;
return x.right;
}
// If both the left and right subtrees of X exist, find the smallest node in the right subtree of X node and replace x node
Node minNode = x.right;
while (minNode.left != null) {
minNode = minNode.left;
}
// Delete minNode node in tree
Node n = x.right;
while (n.left != null) {
if (n.left == minNode) {
n.left = null;
}
n = n.left;
}
// Replace the x node with minNode, and make the left and right subtrees of minNode become the left and right subtrees of x
minNode.left = x.left;
minNode.right = x.right;
// Number of elements - 1
N--;
// Return to replace subtree after deletion ()
x = minNode;
}
return x;
}
// Find the smallest key in the tree
public Key min() {
return min(root).key;
}
// Finds the node where the smallest key in the specified tree is located
private Node min(Node x) {
// Judge whether the x node has left subtree. If it continues to traverse to the left, it is the smallest node
if (x.left != null) {
return min(x.left);
} else {
return x;
}
}
// Find the largest key in the tree
public Key max() {
return max(root).key;
}
// Find the node where the largest key is located in the tree
private Node max(Node x) {
// Judge whether the x node has a right subtree. If it continues to traverse to the left, it is the largest node
if (x.right != null) {
return max(x.right);
} else {
return x;
}
}
// Node class
private class Node {
// Storage key
private Key key;
// Stored value
private Value value;
// Record left child node
private Node left;
// Record right child node
private Node right;
public Node(Key key, Value value, Node left, Node right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
}