preface

Traversal of binary tree is an unavoidable problem to solve the related problems of binary tree. Many problems are solved on the basis of traversal. According to different problems, we can use different traversal methods.
According to the order of operations on the root node, it can be divided into:

• Preorder traversal
• Middle order traversal
• Postorder traversal
• level traversal

According to the way of traversal, it can be divided into:

• Recursion: the code is simple and easy to understand, but it wastes stack memory.
• Iteration: use the auxiliary structure to realize traversal, and the traversal order needs to be designed.

The time complexity of iterating through the array is O(n) and the space complexity is O(h). h is the height of the tree.

The advantage of Morris traversal is that it does not use auxiliary structure to traverse binary tree, and its spatial complexity is O(1).

Why not use auxiliary structure??

First of all, why do we use stacks or queues to help us traverse?
Because the structure of binary tree is that a parent node can easily find a child node, but the child node cannot directly find the parent node. We need to use the stack or queue to keep access records so that we can trace back to the parent node.

Morris traversal uses multiple pointers, so that the parent node can be found through operations with low complexity.

Morris traversal

Morris traversal is a method to save space complexity. Use the null pointer on the leaf node to point to the parent node, and then modify it when traversing this node again, so that the structure of the last binary tree has not changed.

Traversal rule

cur: pointer of current traversal
rightMost: the rightMost node of the left subtree of cur node

1. If the left subtree of cur is empty: cur = cur right;
2. If cur left subtree is not empty: rightMost found
   1. If rightmost Right = null, then make rightmost = cur, cur = cur left;
   2. Otherwise, if it is not empty, it means rightmost Right has been modified. This is the second time we have come to this point to modify rightmost right=null,cur=cur. right;

Explain the above steps:

1. First, go left as a whole. If there is no left subtree, go right.
2. If the left subtree is not empty, find the rightmost node on the left subtree. The right subtree of this node must be empty. Point the null pointer to the current node, that is, save a pointer to the parent node. At this time, the left subtree has no value to access, and cur goes left.
3. The result in 2.2 is that when rightMost traverses this node, the cur pointer will also traverse this node. This is the second access. At this time, when this node is used as rightMost, it has been modified, so we need to modify it to null again.
4. When 2.2 occurs, it means that all the left subtrees of the node have been accessed, so cur goes to the right at this time.
5. The cursor will be modified in order to be valid, and the cursor will be modified in order to be valid.

Illustration

On the whole, it looks like this: if pointer recovery is not considered:

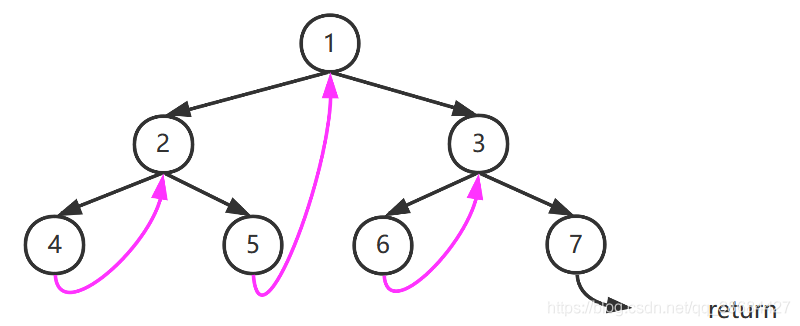
In fact, it is not difficult to find that in this traversal mode, some nodes will visit twice and some nodes will visit once. Because we have two pointers cur and rightMost, cur will walk through all nodes, and rightMost will modify the node direction to make cur revisit a parent node.
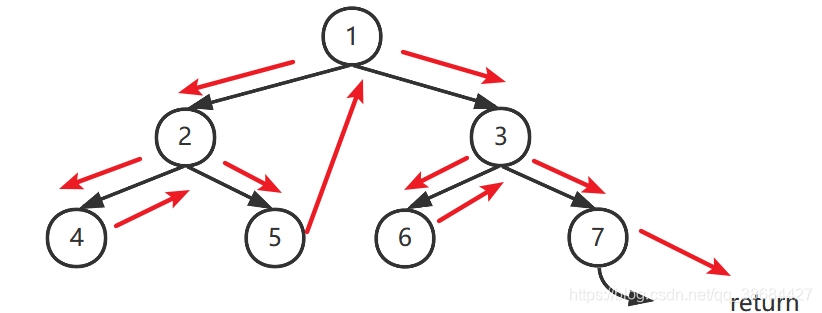
The Mirrors sequence of the binary tree (cur walking order) is:
1 2 4 2 5 1 3 6 3 7

Morris traversal pseudo code

TreeNode cur = root;
while (cur != null) {
// cur pointer to traverse the binary tree
    TreeNode rightMost = cur;
    // Left subtree is not empty
    if (cur.left != null) {
    // Go left to traverse the left subtree
        rightMost = cur.left;
        // Find rightMost
        while (rightMost.right != null && rightMost.right != cur) 
        rightMost = rightMost.right;
        // Check whether the right pointer has been modified
        if (rightMost.right == null) {
            rightMost.right = cur;
            cur = cur.left;
            // If it has not been modified, it means that the left subtree has not been traversed. continue will make it impossible for the lowest cur to move to the right, because we don't want to go to the right. The left subtree has not been traversed yet
            continue;
        } 
        // Yes, this is the second time to this node. We need to modify the pointer of the node back.
        rightMost.right = null;
    }
    // If you've visited, go right
    	cur = cur.right;
}

Based on Morris ergodic preorder

Because there are only two situations for all nodes: one visit and two visits
If a node is visited once, that is, a node without a left subtree, it will be printed.
Nodes visited twice: there is a left subtree, which prints the first time and does not print the second time

public void morrisPreOrder(TreeNode root) {
	if (root == null) return res;
    TreeNode cur = root;
    while (cur != null) {
    	if (cur.left != null) {
   		TreeNode rightMost = cur.left;
    	// Find the rightmost node of cur's left subtree, because we need to return through this node.
    	while (rightMost.right != null && rightMost.right != cur) rightMost = rightMost.right;
    	// When traversing rightMost for the first time, we need to establish its connection with cur and print the cur node at the same time
        if (rightMost.right == null) {
        	// Here is your operation on the node
       		System.out.println(cur.val);
        	rightMost.right = cur;
        	cur = cur.left;
       	 	continue;
        }
        // Restore null pointer of leaf
        rightMost.right = null;
            } else // If the current node has no left child, we don't have to traverse its left subtree. Just output the node and start traversing its right subtree, because we don't have to return to the node
                // Here is your operation on the node
                System.out.println(cur.val);
         cur = cur.right;
        }
}

Middle order based on Morris traversal

If a node is visited once, that is, a node without a left subtree, it will be printed.
Nodes visited twice: there is a left subtree, which will not print for the first time and print for the second time

public void morrisInOrder(TreeNode root) {
	if (root == null) return res;
    TreeNode cur = root;
    while (cur != null) {
    	if (cur.left != null) {
   		TreeNode rightMost = cur.left;
    	// Find the rightmost node of cur's left subtree, because we need to return through this node.
    	while (rightMost.right != null && rightMost.right != cur) rightMost = rightMost.right;
    	// When traversing rightMost for the first time, we need to establish a connection with cur without printing this node
        if (rightMost.right == null) {
        	rightMost.right = cur;
        	cur = cur.left;
       	 	continue;
        }
        // Restore null pointer of leaf
        rightMost.right = null;
        }// If the current node has no left child, we don't have to traverse its left subtree. Just output the node and start traversing its right subtree, because we don't have to return to the node
         // Here is your operation on the node. This is our second visit to this node. Note that there is no else here
         System.out.println(cur.val);
         cur = cur.right;
        }
}

Post order based on Morris traversal

The post order is relatively complex. The overall idea is still based on Morris traversal.
However, no processing will be done for the node visited once.
For the node accessed twice, the right boundary of its left subtree is printed in reverse order during the second access.

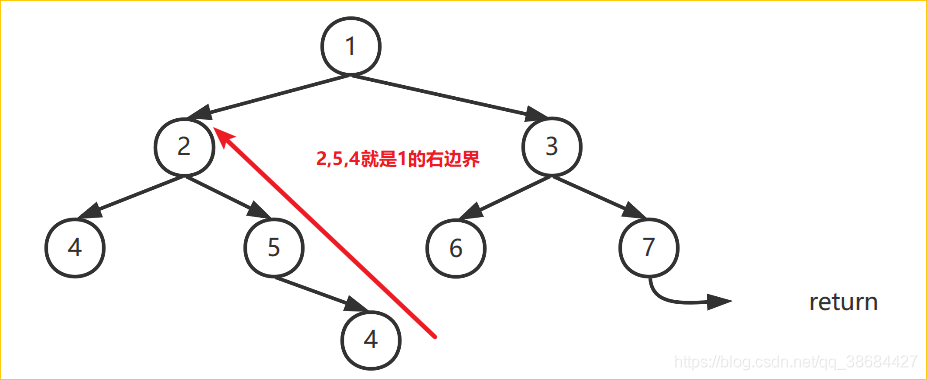
Let's take a look at the left subtree of 1. The sequence of subsequent access is 4,4,5,2. According to the sequence of Morris access, when we come to 4, the right pointer of 4 points to 2. At this time, when we visit node 2 for the second time, we print the right boundary of the left subtree of 2 in reverse order. At this time, we come to 4. Because node 4 is a leaf, the output content is 4.
Then traverse to the following 4 nodes, and the right pointer points to node 1. This is also the second visit to 1. Print in reverse order from 2-5-4 nodes, that is, the right boundary of the left subtree of 1. Note that 1 is not printed at this time.
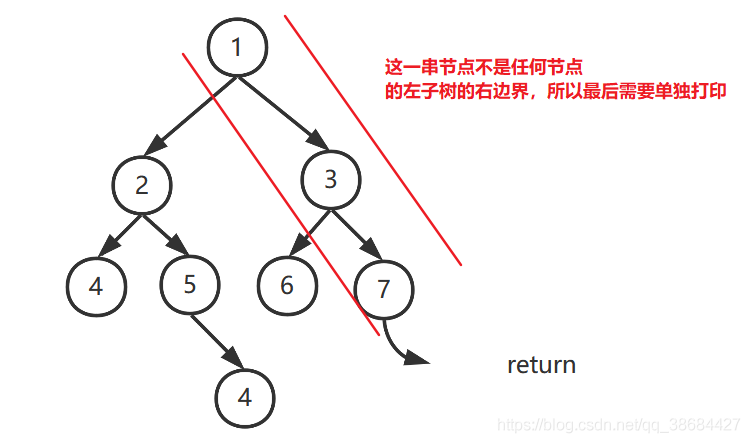
The same is true for the right subtree of the root node, but the right boundary of the root node cannot be printed at last, so you need to print it at last. At this time, the root node is also output, which fully conforms to the result of subsequent traversal.

// Code from leetCode binary tree post traversal
public List<Integer> postorderTraversal(TreeNode root) {
    TreeNode cur = root;
    ArrayList<Integer> res = new ArrayList<>();
    while (cur != null) {
         TreeNode rightMost = cur.left;
         if (rightMost != null) {
             while (rightMost.right != null && rightMost.right != cur)
                 rightMost = rightMost.right;
            if (rightMost.right == null) {
                rightMost.right = cur;
                cur = cur.left;
                continue;
            }
                rightMost.right = null;
                function(cur.left,res);
         }
         	cur = cur.right;
    }
    function(root,res);
    return res;
}
public void function (TreeNode node, ArrayList<Integer> res) {
	//Reverse the entire right boundary first
    TreeNode tail = reverseEdge(node);
    TreeNode cur = tail;
    while (cur != null) {
        res.add(cur.val);
        cur = cur.right;
    }
	//Flip back
    reverseEdge(tail);
}
public TreeNode reverseEdge(TreeNode node) {
    TreeNode pre = null;
    TreeNode next = null;
    while (node != null) {
        next = node.right;
        node.right = pre;
        pre = node;
        node = next;
    }
    return pre;
}

reference resources

Programmer code interview guide (Second Edition)
https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/