1, Binary tree reconstruction

Binary tree reconstruction refers to the reconstruction of binary tree through pre order and middle order, or middle order and post order.

2, Constructing binary tree with middle order and pre order

Two sequences are given:

Preamble: CBADEFGH

Middle order: ABEDFCHG

How to launch the post order?

　

 

First, we know that the traversal order of the preamble is about the root

The traversal order of the middle order is left root right

 

Therefore, the first in the preamble is the root node of the whole root number

Then go to the middle order to match. The left is the left subtree of the root node, and the right is the right subtree of the root node

　　

First time: the root is C

Left subtree: ABEDF

Right subtree: HG

　　

Second time: root is B

Left subtree: A

Right subtree: EDF

　　

The third time: the root is A

Left subtree: None

Right subtree: None

 

The fourth root is D

Left subtree: E

Right subtree: F

 

The fifth root is E

Left subtree: None

Right subtree: None

　　

The sixth root is F

Left subtree: None

Right subtree: None

 

The seventh root is G

Left subtree: H

Right subtree: None

　　

The eighth root is H

Left subtree: None

Right subtree: None

 

The tree diagram is:

　　　　

 

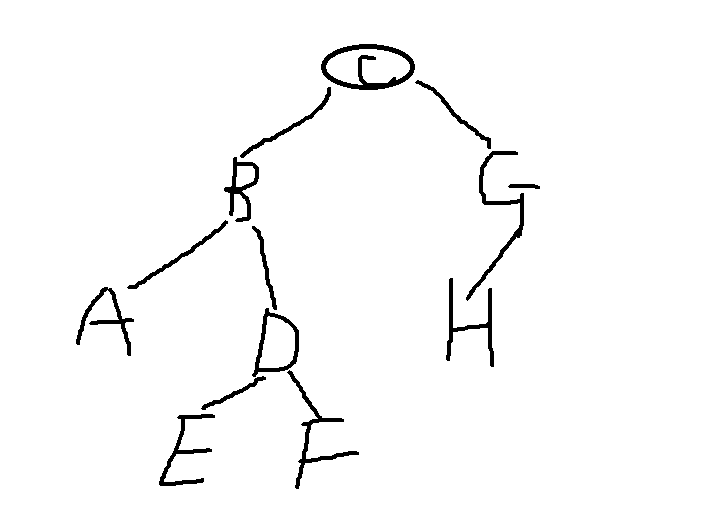
Postorder traversal also looks good: AEFDBHGC

How to implement the code?

　　

Analysis: once the pre order is known, the root node of the left subtree is the previous + 1 every time, and the root node of the right subtree is the root node + 1 found in the middle order traversal. The tree can be reconstructed after repeated. Here I print out the post order directly:

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 char m[110],p[110];//m Is the middle order, p Is the preamble
 4 void printAft(int pmiddle,int ppre,int len) 
 5 {
 6     if(len == 0)//Return to the leaf node
 7         return;
 8     int i = 0;
 9     while(m[pmiddle + i] != p[ppre])//According to the root node, the left and right subtrees of the root node can be found in the middle order
10         i++;
11     //The subsequent printing order is left and right root
12     printAft(pmiddle,ppre + 1,i);//The first represents the starting position of the order in the left subtree, the second represents the subscript of the next root node in the next left subtree, and the third represents the length of the left subtree
13     printAft(pmiddle + i + 1,ppre + i + 1,len - i - 1);//The first represents the starting position of the order in the right subtree, the second represents the position of the next root node in the previous order, and the third represents the length of the right subtree. 0 is the return print root node
14     cout << p[ppre];
15 }
16 int main()
17 {
18     cin >> m;
19     cin >> p;
20     printAft(0,0,strlen(p));
21     return 0;
22 }

　　　　　　　

Realize tree composition and Reprint:

　　

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 char m[110],p[110];//m Is the middle order, p Is the preamble
 4 struct node{
 5     char date;
 6     node *left;
 7     node *right;
 8 };
 9 node *find_Tree(int pmiddle,int ppre,int len) 
10 {
11     if(len == 0)//Return to the leaf node
12         return NULL;
13     int i = 0;
14     node *T = new node();
15     T->date = p[ppre];
16     while(m[pmiddle + i] != p[ppre])//According to the root node, the left and right subtrees of the root node can be found in the middle order
17         i++;
18     T->left = find_Tree(pmiddle,ppre + 1,i);
19     T->right = find_Tree(pmiddle + i + 1,ppre + i + 1,len - i - 1);
20     return T;
21 }
22 void printAft(node *root)
23 {
24     if(root == NULL)
25         return;
26     printAft(root->left);
27     printAft(root->right);
28     cout << root->date;
29 }
30 int main()
31 {
32     cin >> m;
33     cin >> p;
34     node *root;
35     root = find_Tree(0,0,strlen(p));
36     printAft(root);
37     return 0;
38 }

 

3, Middle order and post order construct binary trees (easy to confuse)

The only step to construct a binary tree is to find the root from the last order

Later: AEFDBHGC

Middle order: ABEDFCHG

　　

Practical operation:

The first root is C

Order discovery in search

Left subtree: ABEDF

Right subtree: HG

 

The second root is B

Left subtree: A

Right subtree: EDF

　　

The third root is A

Left subtree: None

Right subtree: None

　　

The fourth root is D

Left subtree: E

Right subtree: F

　　

The fifth root is F (note that this root corresponds to the position of the previous position of the root found in the middle order in the rear order, otherwise it is easy to be confused)

Left subtree: None

Right subtree: None

 

The sixth root is E

Left subtree: None

Right subtree: None

　　

The seventh root is G

Left subtree: H

Right subtree: None

 

The eighth root is H

Left subtree: None

Right subtree: None

 

The tree diagram is:

　　　　

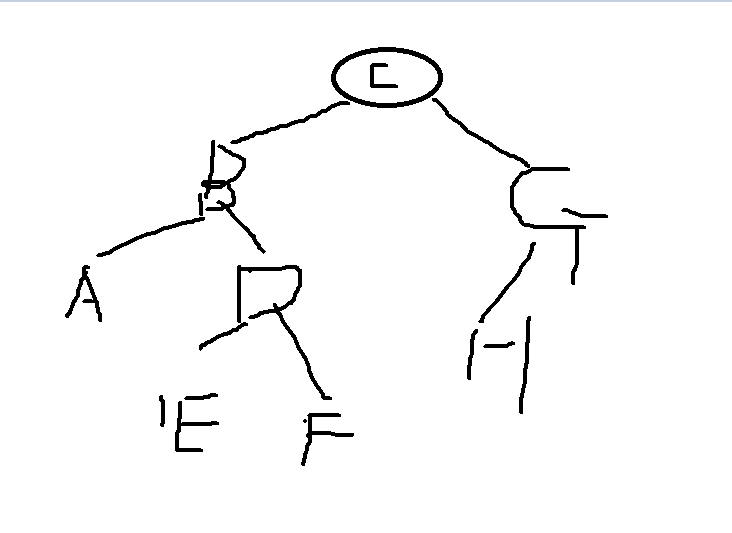
How do you implement the code?

Analysis:

First, we go back and find the first root node

At this time, the start of the left subtree is pre, the next root node is i-1, and the length is i

The right subtree starts at i, the next node is at i+2, and the length is len - i - 1