1, Maximum depth of binary tree

1. Maximum depth of binary tree
   The maximum depth of binary tree can be achieved by recursion, level traversal and depth first traversal, but the simplest and easiest is recursion.

1. Recursive method

1) Determine the three elements of recursion

1. Return value and parameters of recursive function: the return value is the maximum depth of the current node, and the parameters are the current node
2. Single layer logic of recursive function: maximum depth of current node = 1 + maximum depth of left subtree or right subtree
3. Termination condition of recursive function: when the current node is empty, the maximum depth of the current node is 0

2) Recursive method code

class Solution {
public:
	//Recursive parameters and return values
    int maxDepth(TreeNode* root) {
    
    	//Recursive termination condition
        if(root == nullptr) return 0;
        
        //Single layer recursive logic
        int leftdepth = maxDepth(root->left);
        int rightdepth = maxDepth(root->right);
        return 1 + max(leftdepth, rightdepth);
    }
};

2. Hierarchical traversal

The idea of level traversal is very simple. For each layer traversed, let maxdepth + 1. When the traversal is terminated, return maxdepth.

1) Hierarchical traversal code

class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int maxdepth = 0;
        if(root == nullptr) return maxdepth;
        

        que.push(root);
        while(!que.empty()){
            int size = que.size();
            //Traverse the current layer, depth + 1
            maxdepth++;
            for(int i = 0; i < size; i++){
                TreeNode* node = que.front();
                que.pop();
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return maxdepth;
    }
};

3. Depth first traversal

Depth first traversal records the deepest depth encountered in the traversal process and returns it as the maximum depth. This method is not recommended. The code and logic are not clear in hierarchical traversal and recursion.

1) Depth first traversal code

class Solution {
public:
    int maxDepth(TreeNode* root) {
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        int depth = 0;
        int result = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
 
            if (node != NULL) {
                st.pop();
                st.push(node);                          // in
                st.push(NULL);
                //Go down to the next layer, depth + 1
                depth++;
                if (node->right) st.push(node->right);  // right
                if (node->left) st.push(node->left);    // Left

            } else {
                st.pop();
                node = st.top();
                st.pop();
                Access one layer up, depth-1
                depth--;
            }
            //Record the deepest depth encountered during the visit
            result = result > depth ? result : depth;
        }
        return result;

    }
};

2, Maximum depth of N-ary tree

1. Maximum depth of N-ary tree

1. Problem solving ideas

This problem is the generalization of the maximum depth of binary tree. When recursing, we should compare the maximum depth of multiple subtrees

2. Problem solving code

class Solution {
public:
    int maxDepth(Node* root) {
    	//Recursive termination condition
        if(root == nullptr) return 0;
        
        //Recursive single layer logic: Return 1 + maximum depth of subtree
        int maxdepth = 0;
        //Note that for each node, the number of subtrees must be obtained. N cannot be used directly for iteration, otherwise it will cross the boundary
        for(int i = 0; i < root->children.size(); i++){
            maxdepth = max(maxdepth, maxDepth(root->children[i]));
        }    
        return 1 + maxdepth;
    }
};

3, Minimum depth of binary tree

1. Recursive method

1) Determine the three elements of recursion

1. Return value and parameters of recursive function: the return value is the minimum depth of the current node, and the parameters are the current node
2. Single layer logic of recursive function: minimum depth of current node = 1 + minimum depth of left subtree and right subtree
3. Termination condition of recursive function: when the current node is empty, the minimum depth of the current node is 0

However, in single-layer logic, we need to note that when only one subtree is empty, the minimum depth of its two subtrees is not 0, as shown in the figure:

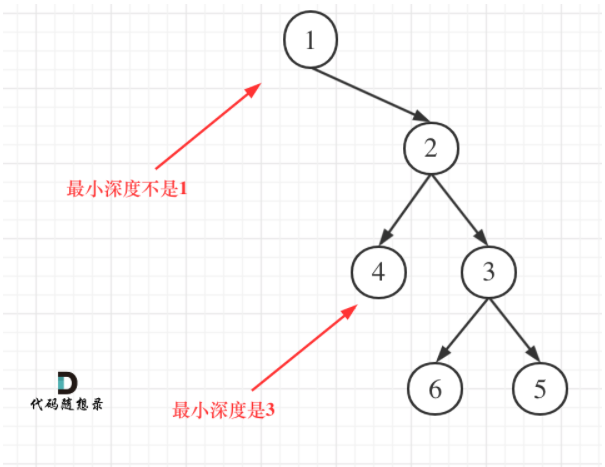
• When the i subtree of node x is empty and the j subtree is not empty, the minimum depth of node x = 1 + the minimum depth of J subtree

2) Recursive code

class Solution {
public:
	//Recursive return values and parameters
    int minDepth(TreeNode* root) {
    
		//Recursive termination condition
        if(root == nullptr) return 0;	
        
        //Recursive single layer logic
        int leftdepth = minDepth(root->left);
        int rightdepth = minDepth(root->right);
        //Processing of empty single subtree
        if(root->left && !root->right) return 1 +leftdepth;
        if(!root->left && root->right) return 1 + rightdepth;
        //Processing of non empty two subtrees
        return 1 + min(leftdepth, rightdepth);
    }
};

2. Iterative method

Traverse the binary tree hierarchically. When the first left and right subtrees are empty, the minimum depth is met, and the depth value at this time is returned

class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int mindepth = 0;
        if(root == nullptr) return mindepth;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            //Start traversing the layer and record the depth + 1
            mindepth++;
            for(int i = 0; i < size; i++){
                TreeNode* node = que.front();
                que.pop();
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
                //If the left and right subtrees are empty, return
                if(!node->left && !node->right) return mindepth;
            }
        }
        return mindepth;
    }
};