1 Principle

1.1 B-tree

(1) m-way lookup tree

An m-way search tree is either an empty tree or a tree satisfying the following properties:

• The root has up to m sub trees and has the following structure:

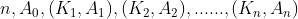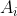,Is a pointer to a subtree,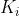The key is,

• In subtree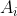All keys in are greater than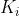, less than.
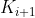• In subtree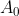All keys in are greater than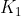
• In subtree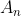All keys in are less than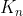
• subtree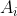m-way lookup tree

(2) B tree

m-order B-tree is an m-way search tree, which is either empty or satisfies the following properties:

• Each node in the tree has at most m sub trees
• The root node has at least two subtrees
• All non terminal nodes except the root node have at least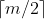subtree
• All leaf nodes are on the same layer

1.2 steps

Specific simulation process reference: https://www.cnblogs.com/pinard/p/6179132.html

References:

BIRCH can identify the imbalance of data distribution in the data set, cluster the points distributed in dense areas and remove the abnormal points distributed in sparse areas. In addition, BIRCH is an incremental clustering method. The clustering decision for each point is based on the currently processed data points rather than the global data points.
① Establish a clustering feature tree
The first is to traverse all the data, and use the given amount of memory and the reclaimed space on the disk to build an initial memory CF tree to reflect the clustering information on the data set. For dense data, it is divided into finer clusters, and sparse data points are removed as outliers.
② Reduce the scope and simplify the clustering feature tree
This process is optional. This part is the bridge connecting step ① and step ③. Similar to step ①, it starts to traverse the leaf nodes of the initialized clustering feature tree, remove more outliers and narrow the range for grouping.
③ Global clustering
Using global clustering or semi global clustering to operate all leaf nodes, the clustering algorithm with data points is easy to adapt to a group of sub clusters, and each sub cluster is represented by its clustering feature vector. Calculate the centroid of sub clusters, and then each sub cluster is represented by centroid, which can capture the main distribution law of data.
④ Cluster refinement
Because step ③ is only a rough summary of the data, and the original data is only scanned once, it is necessary to continue to improve the cluster class. The center of the cluster generated in the previous stage is used as the seed, and the data points are reassigned to the nearest seed to obtain a new set of clusters. This not only allows the migration of points belonging to the sub cluster, but also ensures that all copies of a given data point are migrated to the same sub cluster. It also provides an option to discard outliers. That is, if it is too far from the nearest point, the seed can be treated as an outlier and not included in the result.

2. Parameter description

Function: sklearn cluster. Birch

Parameters:

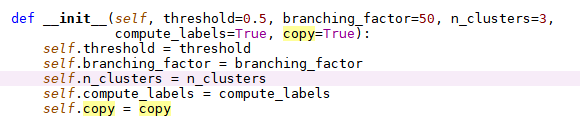
• Threshold: (float,default=0.5) the radius of the merged sub cluster of the new sub cluster and the latest sub cluster is less than the threshold, otherwise it will be split.
• branching_factor: (int,default=50) the maximum number of CF sub clusters in each node.
• n_cluster: (int, default=3) the number of clusters in the final clustering step, if None, the final clustering step is not executed, and the sub clusters are returned as is; if sklearn.cluster.Estimator, the model executes the sub clustering as a new sample.
• compute_labels: (bool,default=True) whether the label value is calculated during each fitting.
• Copy: (bool,default=True) whether to copy the obtained data. If it is set to false, the initialization data will be overwritten.

Properties:

• root_: Root of CF tree
• dummy_leaf_: Pointers to all leaf nodes
• subcluster_centers_: Centroid of sub cluster in all leaves
• subcluster_labels_: Labels of sub cluster centroid after full clustering
• labels_: Labels of all input data

3. Specific implementation

You can refer to the example of scikit learn: https://scikit-learn.org/stable/auto_examples/cluster/plot_birch_vs_minibatchkmeans.html#sphx-glr-auto-examples-cluster-plot-birch-vs-minibatchkmeans-py

4 source code analysis

Source code: anaconda3 / lib / site packages / sklearn / cluster / birch In PY

(1) Prefix knowledge

• The hasattr() function is used to judge whether a class instance object contains a property or method with a specified name, and returns True and False

hasattr(obj, name), where obj refers to the instance object of a class, and name refers to the specified attribute name or method name.

• The getattr() function gets the value of the specified attribute in a class instance object

getattr(obj, name[, default]), where obj represents the specified class instance object, name represents the specified attribute name, and default is an optional parameter, which is used to set the default return value of the function. That is, when the function fails to find, if the default parameter is not specified, the program will directly report an AttributeError error error, otherwise the function will return the value specified by default.

• The function of setattr() is relatively complex. Its most basic function is to modify the attribute value in the class instance object. Secondly, it can also dynamically add properties or methods for instance objects.

(2) Birch function

• Birch (baseestimator, transformer mixin, clustermixin) is in the base file of sklearn
• Other parameters

• fit function (the main core calculation is in _fitfunction)

 def fit(self, X, y=None):
        """
        Build a CF Tree for the input data.

        Parameters
        ----------
        X : {array-like, sparse matrix} of shape (n_samples, n_features)
            Input data.

        y : Ignored
            Not used, present here for API consistency by convention.

        Returns
        -------
        self
            Fitted estimator.
        """
        self.fit_, self.partial_fit_ = True, False
        return self._fit(X)

    def _fit(self, X):
        
        X = self._validate_data(X, accept_sparse='csr', copy=self.copy)
        
        threshold = self.threshold
        branching_factor = self.branching_factor

        if branching_factor <= 1:
            raise ValueError("Branching_factor should be greater than one.")
        n_samples, n_features = X.shape

        # If partial_fit is called for the first time or fit is called, we
        # start a new tree.
        partial_fit = getattr(self, 'partial_fit_')
        has_root = getattr(self, 'root_', None)
        if getattr(self, 'fit_') or (partial_fit and not has_root):
            # The first root is the leaf. Manipulate this object throughout.
            self.root_ = _CFNode(threshold=threshold,
                                 branching_factor=branching_factor,
                                 is_leaf=True,
                                 n_features=n_features)

            # To enable getting back subclusters.
            self.dummy_leaf_ = _CFNode(threshold=threshold,
                                       branching_factor=branching_factor,
                                       is_leaf=True, n_features=n_features)
            self.dummy_leaf_.next_leaf_ = self.root_
            self.root_.prev_leaf_ = self.dummy_leaf_

        # Cannot vectorize. Enough to convince to use cython.
        if not sparse.issparse(X):
            iter_func = iter
        else:
            iter_func = _iterate_sparse_X
        
        #Traverse the data and construct sub clusters
        for sample in iter_func(X):
            
            subcluster = _CFSubcluster(linear_sum=sample)
            split = self.root_.insert_cf_subcluster(subcluster)
            #If the CF is determined to be split, use the split algorithm to return two sub clusters and add the sub clusters to the root
            if split:
                new_subcluster1, new_subcluster2 = _split_node(
                    self.root_, threshold, branching_factor)
                del self.root_
                self.root_ = _CFNode(threshold=threshold,
                                     branching_factor=branching_factor,
                                     is_leaf=False,
                                     n_features=n_features)
                self.root_.append_subcluster(new_subcluster1)
                self.root_.append_subcluster(new_subcluster2)
        #Get the centroid of leaf node
        centroids = np.concatenate([
            leaf.centroids_ for leaf in self._get_leaves()])
        self.subcluster_centers_ = centroids

        self._global_clustering(X)
        return self

Other functions:

Sparse matrix construction

def _iterate_sparse_X(X):
    """This little hack returns a densified row when iterating over a sparse
    matrix, instead of constructing a sparse matrix for every row that is
    expensive.
    """
    n_samples = X.shape[0]
    X_indices = X.indices
    X_data = X.data
    X_indptr = X.indptr
    
    for i in range(n_samples):
        row = np.zeros(X.shape[1])
        startptr, endptr = X_indptr[i], X_indptr[i + 1]
        nonzero_indices = X_indices[startptr:endptr]
        row[nonzero_indices] = X_data[startptr:endptr]
        yield row

Function of splitting leaf nodes: define two sub clusters and two CF nodes, and add the CF node to the CF sub cluster. If the incoming sub cluster is a leaf node, carry out a series of pointer transformations, calculate the distance between the centroid and the sum of squares of the sub cluster, select the matrix with the largest distance, and then select the smaller value as a sub cluster, The others belong to another sub cluster.

def _split_node(node, threshold, branching_factor):
    """The node has to be split if there is no place for a new subcluster
    in the node.
    1. Two empty nodes and two empty subclusters are initialized.
    2. The pair of distant subclusters are found.
    3. The properties of the empty subclusters and nodes are updated
       according to the nearest distance between the subclusters to the
       pair of distant subclusters.
    4. The two nodes are set as children to the two subclusters.
    """
    new_subcluster1 = _CFSubcluster()
    new_subcluster2 = _CFSubcluster()
    new_node1 = _CFNode(
        threshold=threshold, branching_factor=branching_factor,
        is_leaf=node.is_leaf,
        n_features=node.n_features)
    new_node2 = _CFNode(
        threshold=threshold, branching_factor=branching_factor,
        is_leaf=node.is_leaf,
        n_features=node.n_features)
    new_subcluster1.child_ = new_node1
    new_subcluster2.child_ = new_node2

    if node.is_leaf:
        if node.prev_leaf_ is not None:
            node.prev_leaf_.next_leaf_ = new_node1
        new_node1.prev_leaf_ = node.prev_leaf_
        new_node1.next_leaf_ = new_node2
        new_node2.prev_leaf_ = new_node1
        new_node2.next_leaf_ = node.next_leaf_
        if node.next_leaf_ is not None:
            node.next_leaf_.prev_leaf_ = new_node2

    dist = euclidean_distances(
        node.centroids_, Y_norm_squared=node.squared_norm_, squared=True)
    n_clusters = dist.shape[0]

    farthest_idx = np.unravel_index(
        dist.argmax(), (n_clusters, n_clusters))
    node1_dist, node2_dist = dist[(farthest_idx,)]

    node1_closer = node1_dist < node2_dist
    for idx, subcluster in enumerate(node.subclusters_):
        if node1_closer[idx]:
            new_node1.append_subcluster(subcluster)
            new_subcluster1.update(subcluster)
        else:
            new_node2.append_subcluster(subcluster)
            new_subcluster2.update(subcluster)
    return new_subcluster1, new_subcluster2

Get leaf node:

    def _get_leaves(self):
        """
        Retrieve the leaves of the CF Node.

        Returns
        -------
        leaves : list of shape (n_leaves,)
            List of the leaf nodes.
        """
        leaf_ptr = self.dummy_leaf_.next_leaf_
        leaves = []
        while leaf_ptr is not None:
            leaves.append(leaf_ptr)
            leaf_ptr = leaf_ptr.next_leaf_
        return leaves

Global clustering: agglomerative clustering algorithm is added (written separately).

def _global_clustering(self, X=None):
        """
        Global clustering for the subclusters obtained after fitting
        """
        clusterer = self.n_clusters
        centroids = self.subcluster_centers_
        compute_labels = (X is not None) and self.compute_labels

        # Preprocessing for the global clustering.
        not_enough_centroids = False
        if isinstance(clusterer, numbers.Integral):
            clusterer = AgglomerativeClustering(
                n_clusters=self.n_clusters)
            # There is no need to perform the global clustering step.
            if len(centroids) < self.n_clusters:
                not_enough_centroids = True
        elif (clusterer is not None and not
              hasattr(clusterer, 'fit_predict')):
            raise ValueError("n_clusters should be an instance of "
                             "ClusterMixin or an int")

        # To use in predict to avoid recalculation.
        self._subcluster_norms = row_norms(
            self.subcluster_centers_, squared=True)

        if clusterer is None or not_enough_centroids:
            self.subcluster_labels_ = np.arange(len(centroids))
            if not_enough_centroids:
                warnings.warn(
                    "Number of subclusters found (%d) by Birch is less "
                    "than (%d). Decrease the threshold."
                    % (len(centroids), self.n_clusters), ConvergenceWarning)
        else:
            # The global clustering step that clusters the subclusters of
            # the leaves. It assumes the centroids of the subclusters as
            # samples and finds the final centroids.
            self.subcluster_labels_ = clusterer.fit_predict(
                self.subcluster_centers_)

        if compute_labels:
            self.labels_ = self.predict(X)

 

(3)CFNode

parameter		attribute
threshold:float	Determine the threshold of sub cluster	subclusters_ : list	Sub cluster of specified nodes
branching_factor: int	Branching factor	prev_leaf_ : _CFNode	Front leaf node
is_leaf : bool	Is it a leaf node	next_leaf_ : _CFNode	Posterior leaf node
n_features : int	Feature quantity	init_centroids_	Initialize centroid, shape=(branching_factor + 1, n_features)
		init_sq_norm_	Initialize sum of squares, shape=(branching_factor + 1, n_features)
		centroids_	centroid
		squared_norm_	Sum of squares

 

CFNode consists of three functions:

First function: append_subcluster(self, subcluster) updates the characteristic value of CF

    def append_subcluster(self, subcluster):
        #Get the sub cluster length of CF
        n_samples = len(self.subclusters_)
        #Add new sub clusters to CF
        self.subclusters_.append(subcluster)
        #Initialize the sum of centroids and squares of new sub clusters (add centroids and squares to the list)
        self.init_centroids_[n_samples] = subcluster.centroid_
        self.init_sq_norm_[n_samples] = subcluster.sq_norm_

        # Keep centroids and squared norm as views. In this way
        # if we change init_centroids and init_sq_norm_, it is
        # sufficient,
        #Update the sum of centroids and squares of the final sub clusters (add centroids and squares to the list)
        self.centroids_ = self.init_centroids_[:n_samples + 1, :]
        self.squared_norm_ = self.init_sq_norm_[:n_samples + 1]

The second function: update_split_subclusters(self, subcluster,new_subcluster1, new_subcluster2): update split nodes

def update_split_subclusters(self, subcluster,
                                 new_subcluster1, new_subcluster2):
        """Remove a subcluster from a node and update it with the
        split subclusters.
        """
        ind = self.subclusters_.index(subcluster)
        self.subclusters_[ind] = new_subcluster1
        self.init_centroids_[ind] = new_subcluster1.centroid_
        self.init_sq_norm_[ind] = new_subcluster1.sq_norm_
        self.append_subcluster(new_subcluster2)

The third function: Insert_ cf_ Sub cluster (self, sub cluster): insert CF features into sub clusters

 def insert_cf_subcluster(self, subcluster):
        """Insert a new subcluster into the node."""
        # self.subclusters_ If it does not exist, the new sub cluster will be added to the sub cluster list
        if not self.subclusters_:
            self.append_subcluster(subcluster)
            return False
        threshold = self.threshold
        branching_factor = self.branching_factor
        # We need to find the closest subcluster among all the
        # subclusters so that we can insert our new subcluster.
        #Calculate distance matrix
        dist_matrix = np.dot(self.centroids_, subcluster.centroid_)
        dist_matrix *= -2.
        dist_matrix += self.squared_norm_
        closest_index = np.argmin(dist_matrix)
        closest_subcluster = self.subclusters_[closest_index]

        # If the subcluster has a child, we need a recursive strategy.
        #If there is handwriting in the sub cluster, the recursive strategy needs to be adopted to update the CF parameters
        if closest_subcluster.child_ is not None:
            split_child = closest_subcluster.child_.insert_cf_subcluster(
                subcluster)

            if not split_child:
                # If it is determined that the child need not be split, we
                # can just update the closest_subcluster
                closest_subcluster.update(subcluster)
                self.init_centroids_[closest_index] = \
                    self.subclusters_[closest_index].centroid_
                self.init_sq_norm_[closest_index] = \
                    self.subclusters_[closest_index].sq_norm_
                return False

            # things not too good. we need to redistribute the subclusters in
            # our child node, and add a new subcluster in the parent
            # subcluster to accommodate the new child.
            else:
                new_subcluster1, new_subcluster2 = _split_node(
                    closest_subcluster.child_, threshold, branching_factor)
                self.update_split_subclusters(
                    closest_subcluster, new_subcluster1, new_subcluster2)

                if len(self.subclusters_) > self.branching_factor:
                    return True
                return False

        # good to go!
        
        else:
            #When the residual radius of the sub cluster is less than the threshold, the CF parameter is updated
            merged = closest_subcluster.merge_subcluster(
                subcluster, self.threshold)
            #If merged exists, add a new sub cluster to the sub cluster and update the parameters of the sub cluster
            if merged:
                self.init_centroids_[closest_index] = \
                    closest_subcluster.centroid_
                self.init_sq_norm_[closest_index] = \
                    closest_subcluster.sq_norm_
                return False

            # not close to any other subclusters, and we still
            # have space, so add.
            #If the CF tree of the sub cluster exceeds the number of branch factors, it will be split into new sub clusters and added to the Node
            elif len(self.subclusters_) < self.branching_factor:
                self.append_subcluster(subcluster)
                return False

            # We do not have enough space nor is it closer to an
            # other subcluster. We need to split.
            else:
                self.append_subcluster(subcluster)
                return True

(4)CFSubcluster

parameter		attribute
linear_sum:narray	sample	n_samples_ :int	Number of samples per sub cluster
		linear_sum_ : narray	Linear sum of all samples in sub cluster
		squared_sum_ : float	Sum of the squared l2 norms
		centroids_	centroid
		child_	Child node
		sq_norm_	Sum of squares of sub clusters

CFSubcluster consists of three functions:

The first function: update(self, subcluster) updates the values (linear sum, centroid, square sum, etc.)

def update(self, subcluster):
        self.n_samples_ += subcluster.n_samples_
        self.linear_sum_ += subcluster.linear_sum_
        self.squared_sum_ += subcluster.squared_sum_
        self.centroid_ = self.linear_sum_ / self.n_samples_
        self.sq_norm_ = np.dot(self.centroid_, self.centroid_)

The second function: Merge_ Sub cluster (self, sub cluster)

def merge_subcluster(self, nominee_cluster, threshold):
        """Check if a cluster is worthy enough to be merged. If
        yes then merge.
        """
        new_ss = self.squared_sum_ + nominee_cluster.squared_sum_
        new_ls = self.linear_sum_ + nominee_cluster.linear_sum_
        new_n = self.n_samples_ + nominee_cluster.n_samples_
        new_centroid = (1 / new_n) * new_ls
        new_norm = np.dot(new_centroid, new_centroid)
        dot_product = (-2 * new_n) * new_norm
        sq_radius = (new_ss + dot_product) / new_n + new_norm
        if sq_radius <= threshold ** 2:
            (self.n_samples_, self.linear_sum_, self.squared_sum_,
             self.centroid_, self.sq_norm_) = \
                new_n, new_ls, new_ss, new_centroid, new_norm
            return True
        return False

The third function: radius(self): calculate the residual

def radius(self):
        """Return radius of the subcluster"""
        dot_product = -2 * np.dot(self.linear_sum_, self.centroid_)
        return sqrt(
            ((self.squared_sum_ + dot_product) / self.n_samples_) +
            self.sq_norm_)