premise
The main content of this paper is to analyze the Java implementation of BitMap in JDK util. The source code implementation of BitSet is written based on JDK11. Other versions of JDK are not necessarily suitable.
The low bit of the figure in this paper should actually be on the right, but in order to improve the reading experience, the author changed the low bit to the left.
What is BitMap
BitMap, translated as BitMap, is a data structure that represents a Dense Set in a finite field. Each element appears at least once, and no other data is associated with the element. It is widely used in indexing, data compression and so on (from Wikipedia entries). In the computer, 1 byte = 8 bit s. A bit (bit, called bit or bit) can represent two values of 1 or 0. A bit is used to mark the value of an element, and KEY or INDEX is the element to form a mapping diagram. Because bit is used as the unit of underlying data storage, it can greatly save storage space.
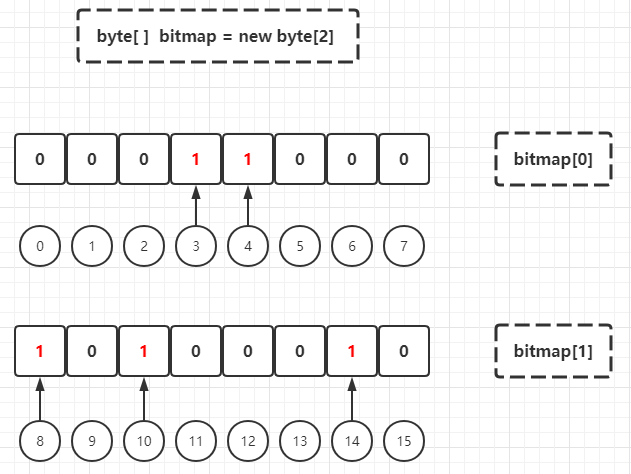
In Java, an int type integer accounts for 4 bytes and 16 bits. The maximum value of int is more than 2 billion (specifically 2147483647). Suppose there is a requirement to judge whether an integer m exists among 2 billion integers. It is required that the memory used must be less than or equal to 4GB. If each integer is stored by int, 2 billion * 4byte /1024/1024/1024 is required to store 2 billion integers, which is about 7.45GB, which obviously can not meet the requirements. If BitMap is used, only 2 billion bit memory is required, that is, 2 billion / 8 / 1024 / 1024 / 1024 is about 0.233GB. In the case of a large amount of data, the data set has a limited state, so BitMap storage and subsequent calculation can be considered. Now assume that the byte array is used as the underlying storage structure of BitMap, and initialize a BitMap instance with a capacity of 16. The example is as follows:
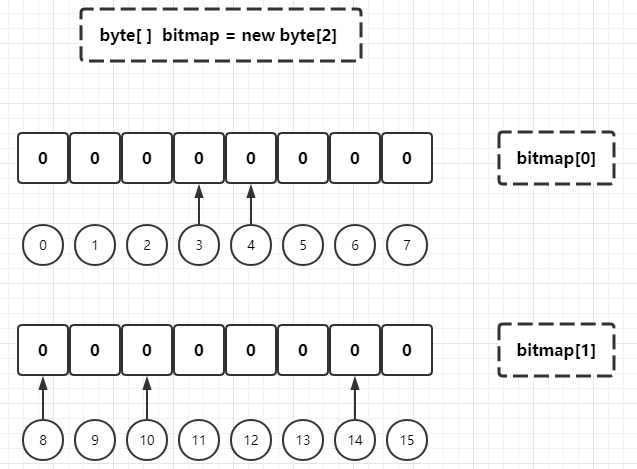
It can be seen that the current byte array has two elements: bitmap[0] (virtual subscript [0,7]) and bitmap[1] (virtual subscript [8,15]). Here, it is assumed that the BitMap instance constructed above is used to store the customer ID and customer gender relationship (bit 1 represents male and bit 0 represents female), and the male customer with ID equal to 3 and the female customer with ID equal to 10 are added to the BitMap:
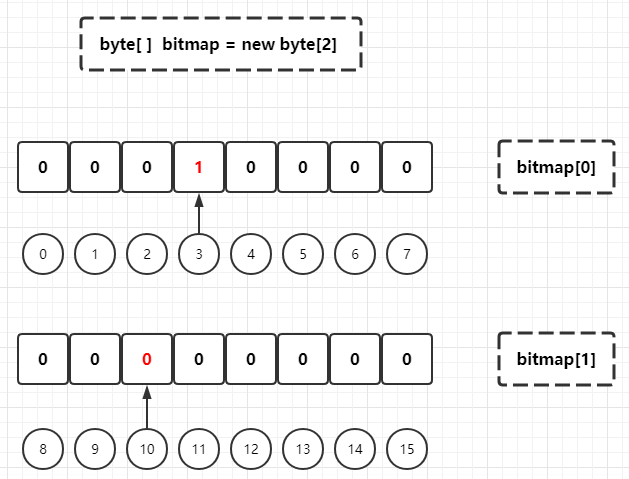
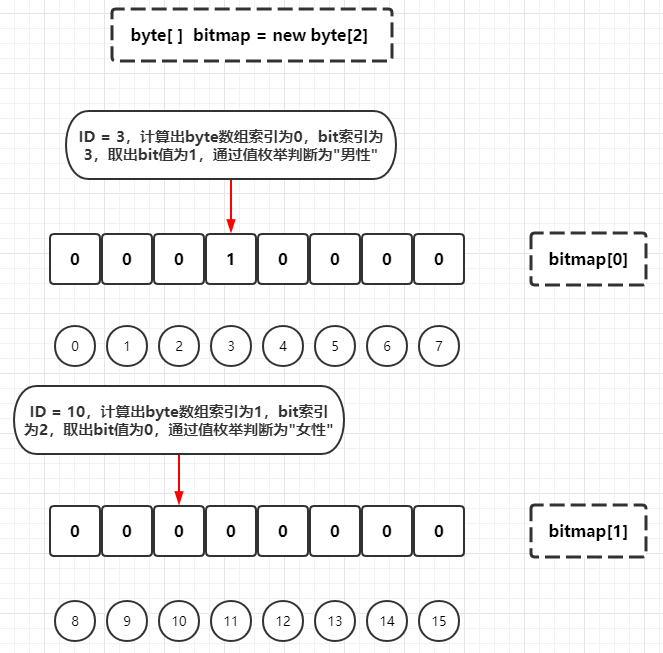
Since 1 byte = 8 bit s, the byte array index to be stored can be located by dividing the customer ID by 8, and then the specific bit index in the byte array to be stored can be obtained by taking the module based on 8 through the customer ID:
# Male customer with ID equal to 3 Logical index = 3 byte Array index = 3 / 8 = 0 bit Indexes = 3 % 8 = 3 => That is, it needs to be stored in byte[0]On a bit with a subscript of 3, the bit is set to 1 # Female customer with ID equal to 10 Logical index = 10 byte Array index = 10 / 8 = 1 bit Indexes = 10 % 8 = 2 => That is, it needs to be stored in byte[1]On a bit with a subscript of 2, the bit is set to 0
Then judge the gender of customers with customer ID 3 or 10 respectively:
If a male user with customer ID 17 is added at this time, since the old BitMap can only store 16 bits, it needs to be expanded. Judge that only one byte element (byte[2]) needs to be added to the byte array:
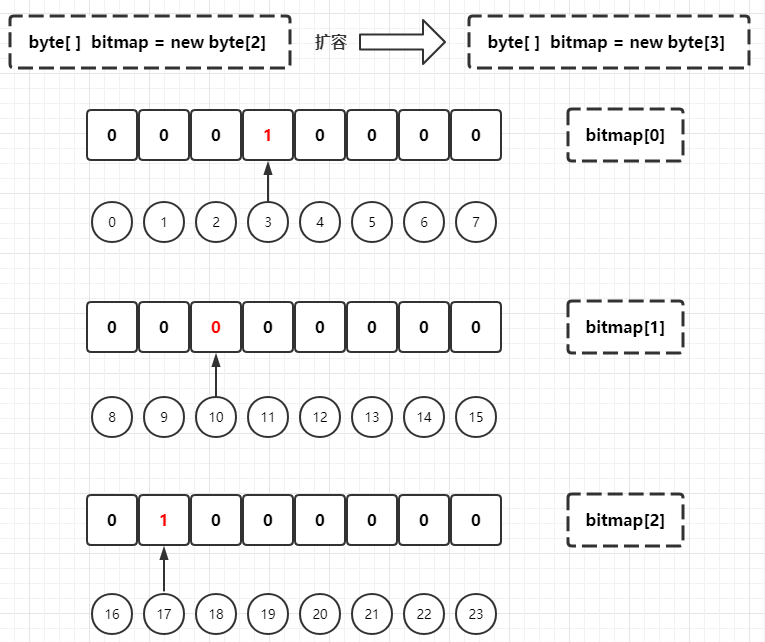
In principle, the bottom byte array can be continuously expanded when the length of byte array reaches integer MAX_ Value, the capacity of BitMap has reached the maximum value.
BitSet easy to use
java. util. Although BitSet is called Set in name, it is actually the BitMap implementation built in JDK. 1 this class is a very old class. From the annotation, it is jdk1 0, but most methods are jdk1 Newly added or updated after 4. The example in the previous section makes a Demo based on BitSet:
public class BitSetApp {
public static void main(String[] args) {
BitSet bitmap = new BitSet(16);
bitmap.set(3, Boolean.TRUE);
bitmap.set(11, Boolean.FALSE);
System.out.println("Index 3 of bitmap => " + bitmap.get(3));
System.out.println("Index 11 of bitmap => " + bitmap.get(11));
bitmap.set(17, Boolean.TRUE);
// Capacity expansion will not be triggered here because the underlying storage array in BitSet is long []
System.out.println("Index 17 of bitmap => " + bitmap.get(17));
}
}
// Output results
Index 3 of bitmap => true
Index 11 of bitmap => false
Index 17 of bitmap => true
The API is relatively simple to use. In order to meet other scenarios, BitSet also provides several practical static factory methods for instance construction, range setting and clearing bit values and some set operations. There are no examples here. It will be expanded in detail when analyzing the source code later.
BitSet source code analysis
As mentioned earlier, if BitMap uses byte array storage, when the logical subscript of the newly added element exceeds the maximum logical subscript of the initialized byte array, it must be expanded. In order to reduce the number of capacity expansion as much as possible, in addition to defining the initialized underlying storage structure according to the actual situation, we should also select a data type array that can "carry" more bits. Therefore, in BitSet, the underlying storage structure selects a long array. A long integer accounts for 64 bits and the bit length is 8 times that of a byte integer, In scenarios with a large range of data to be processed, the number of capacity expansion can be effectively reduced. In order to simplify the analysis process, we will use as few elements as possible to simulate the changes of the underlying long array. There are some notes on the design at the top of BitSet, which are briefly listed and summarized as follows:
- BitSet is an implementation of an increasable bit vector. In design, each bit is a Boolean value, and the logical index of bits is a nonnegative integer
- The initialization value of all bits of BitSet is false (integer 0)
- The size attribute of BitSet is related to its implementation, and the length attribute (logical length of bit table) is independent of its implementation
- BitSet is designed to be non thread safe and requires additional synchronization in a multi-threaded environment
According to the habit of analyzing source code in the past, first look at all core member properties of BitSet:
public class BitSet implements Cloneable, java.io.Serializable {
// Words is a long array. A long integer is 64bit, 2 ^ 6 = 64. Here, 6 is selected as the addressing parameter of words, which can quickly locate the element index in specific words based on the logical subscript
private static final int ADDRESS_BITS_PER_WORD = 6;
// The number of bits per element in words. The decimal value is 64
private static final int BITS_PER_WORD = 1 << ADDRESS_BITS_PER_WORD;
// bit subscript mask, decimal value is 63
private static final int BIT_INDEX_MASK = BITS_PER_WORD - 1;
// Mask, decimal value - 1, that is, 64 bits are all 1, which is used for the left or right shift of some word masks
private static final long WORD_MASK = 0xffffffffffffffffL;
/**
* Serialization correlation, skipping
*/
private static final ObjectStreamField[] serialPersistentFields = {
new ObjectStreamField("bits", long[].class),
};
/**
* The underlying bit storage structure, the long array, is also the corresponding value of the serialized field "bits"
*/
private long[] words;
/**
* The number of elements in the used words array, note translation: the number of words (elements of words) in the logical length of the current BitSet, instantaneous value
*/
private transient int wordsInUse = 0;
/**
* Mark whether the length of the words array is the same as that of the user
*/
private transient boolean sizeIsSticky = false;
// Serial version number used by JDK 1.0.2
private static final long serialVersionUID = 7997698588986878753L;
// Other methods are temporarily omitted
}
Next, let's look at some auxiliary methods of BitSet:
// bit based logical subscript locates the index of word element in words and directly shifts it to the right by 6 bits
// For example: bitIndex = 3, then bitindex > > address_ BITS_ PER_ Word = > 0, the description locates to words[0]
// For example: bitIndex = 35, then bitindex > > address_ BITS_ PER_ Word = > 1, the description locates to words[1]
private static int wordIndex(int bitIndex) {
return bitIndex >> ADDRESS_BITS_PER_WORD;
}
// Each public method must retain these invariants and verify the identity of internal variables, which literally means that each public method must call this identity verification
// First identity: the current BitSet is empty or the last words element cannot be 0 (in fact, the current BitSet is not empty)
// The second identity: wordsInUse boundary check. The range is [0, words.length]
// The third identity: wordsInUse or equal to words Length means that all words elements are used; Or words[wordsInUse] == 0, which means that none of the elements in words with the index [wordsInUse, words.length - 1] are used
private void checkInvariants() {
assert(wordsInUse == 0 || words[wordsInUse - 1] != 0);
assert(wordsInUse >= 0 && wordsInUse <= words.length);
assert(wordsInUse == words.length || words[wordsInUse] == 0);
}
// Recalculate the value of wordsInUse, that is, refresh the calculated value of the used words element
// Based on the current wordsInUse - 1, traverse forward to i = 0, find the latest words[i] that is not 0, and then re assign it to i + 1, where I is the index of the words array
// wordsInUse is actually the subscript of the last non-zero element of the words array plus 1, or the number of elements of words used, which is called logical size
private void recalculateWordsInUse() {
// Traverse the bitset until a used word is found
int i;
for (i = wordsInUse-1; i >= 0; i--)
if (words[i] != 0)
break;
wordsInUse = i+1; // The new logical size
}
Then look at BitSet constructor and static factory method:
// The default public construction method is that the logical length of the bit table is 64, the length of the words array is 2, and the flag sizeIsSticky is false, that is, the length of the bit table is not user-defined
public BitSet() {
initWords(BITS_PER_WORD);
sizeIsSticky = false;
}
// The construction method of custom bit table logical length. The length must be a non negative integer and the flag sizeIsSticky is true, that is, the length of the bit table is user-defined
public BitSet(int nbits) {
if (nbits < 0)
throw new NegativeArraySizeException("nbits < 0: " + nbits);
initWords(nbits);
sizeIsSticky = true;
}
// Initialize the words array. The length of the array is length = (nbits - 1) / 64 + 1
// For example, nbits = 16, which is equivalent to long [] words = new long [(16 - 1) / 64 + 1] = > new long [1];
// For example, nbits = 65 is equivalent to long [] words = new long [(65 - 1) / 64 + 1] = > new long [2];
// and so on
private void initWords(int nbits) {
words = new long[wordIndex(nbits-1) + 1];
}
// Directly customize the underlying words array construction method, and mark all words elements to be used
private BitSet(long[] words) {
this.words = words;
this.wordsInUse = words.length;
checkInvariants();
}
// Directly customize the construction method of the underlying words array. This construction method is different from the previous method. It will traverse from the input parameter long array to the first element or the element that is not 0. In this way, you can cut off the useless high-order 0 elements as much as possible
// In short, it is equivalent to BitSet Valueof (new long [] {1L, 0l}) = remove the following 0 element = > BitSet valueOf(new long[]{1L})
public static BitSet valueOf(long[] longs) {
int n;
for (n = longs.length; n > 0 && longs[n - 1] == 0; n--)
;
return new BitSet(Arrays.copyOf(longs, n));
}
// Directly customize the underlying words array construction method. The input parameter is required to be of LongBuffer type. LongBuffer = > long [] words is required. The method is consistent with BitSet valueof (long [] long) processing logic
public static BitSet valueOf(LongBuffer lb) {
lb = lb.slice();
int n;
for (n = lb.remaining(); n > 0 && lb.get(n - 1) == 0; n--)
;
long[] words = new long[n];
lb.get(words);
return new BitSet(words);
}
// The following two construction methods are based on byte array, traversing from the back until the first element or element not 0 is traversed, truncating a new array, and then converting it into a long array to construct BitSet instances
public static BitSet valueOf(byte[] bytes) {
return BitSet.valueOf(ByteBuffer.wrap(bytes));
}
public static BitSet valueOf(ByteBuffer bb) {
// Small end byte sorting
bb = bb.slice().order(ByteOrder.LITTLE_ENDIAN);
int n;
// The first element or the first element that is not 0 is obtained from the backward forward traversal
for (n = bb.remaining(); n > 0 && bb.get(n - 1) == 0; n--)
;
// Here, we need to consider the case that the number of byte elements in the byte container is not a multiple of 8
long[] words = new long[(n + 7) / 8];
// Truncate the following 0 elements
bb.limit(n);
int i = 0;
// When the number of remaining elements is greater than or equal to 8, read according to 64 bits
while (bb.remaining() >= 8)
words[i++] = bb.getLong();
// When the number of remaining elements is less than 8, it is read according to byte and filled into the long array element through mask calculation and left shift
for (int remaining = bb.remaining(), j = 0; j < remaining; j++)
words[i] |= (bb.get() & 0xffL) << (8 * j);
return new BitSet(words);
}
The source code of the constructor here is not very complex, but the static factory method BitSet valueOf(ByteBuffer bb) is cumbersome. Here is an example:
ByteBuffer byteBuffer = ByteBuffer.allocate(10); byteBuffer.order(ByteOrder.LITTLE_ENDIAN); byteBuffer.putLong(1L); byteBuffer.put((byte)3); byteBuffer.put((byte)1); byteBuffer.flip(); BitSet bitSet = BitSet.valueOf(byteBuffer); System.out.println(bitSet.size()); System.out.println(bitSet.length()); // Output results 128 73
The process is as follows:
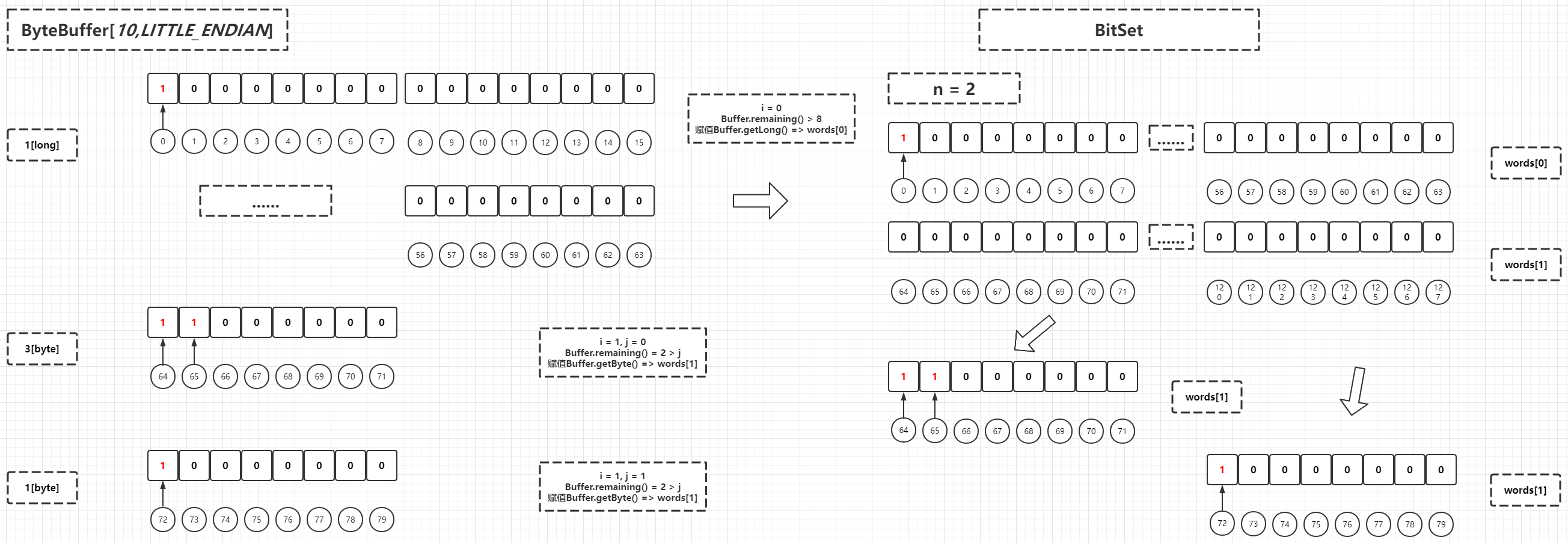
Next, look at the conventional set, get and clear methods:
// Sets the bit of the specified logical index to true
public void set(int bitIndex) {
// Bit logical index must be greater than or equal to 0
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
// Calculates the index of the words array element
int wordIndex = wordIndex(bitIndex);
// Judge whether to expand the capacity. If necessary, expand the words array
expandTo(wordIndex);
// Equivalent to words [wordindex] = words [wordindex] | (1L < < bitindex)
// Note that if the left shift of long exceeds 63 bits, it will overflow, that is, 1L < < 64 = > 1L, 1L < < 65 = > 1L < < 1,1l < < 66 = > 1L < < 2 and so on
// Here, it is equivalent to or calculating the left shift result directly with the corresponding words element. Because the former shifts left based on 1, the binary number must be a 64 bit binary sequence with only one bit of 1 and other bits of 0, or the operation will set the bit value of 1 corresponding to the corresponding words element to 1 and re assign the corresponding words element
// Similar to this: 0000 0000 | 0000 1000 = > 0000 1000
words[wordIndex] |= (1L << bitIndex); // Restores invariants
// Invariant identity Assertion Verification
checkInvariants();
}
// Expand the capacity based on the subscript of the calculated words array element
private void expandTo(int wordIndex) {
// Calculates the length of the words Array required for the subscript of the current words element
int wordsRequired = wordIndex + 1;
// If the length of the words Array required for the subscript of the current words element is greater than the number of elements in the currently used words array, the capacity will be expanded (the array may not be expanded, and there is a layer of judgment in the capacity expansion method)
if (wordsInUse < wordsRequired) {
// Expand the capacity based on the required words array length
ensureCapacity(wordsRequired);
// Resets the number of elements in the currently used words array
wordsInUse = wordsRequired;
}
}
// Expand the capacity based on the calculated words array element subscript, and copy the array on the premise that it meets the requirements
private void ensureCapacity(int wordsRequired) {
// If the length of the current words array is smaller than the required words array, expand the capacity
if (words.length < wordsRequired) {
// The length of the allocated new array is the maximum between the old words array element and the length of the passed in required words array
int request = Math.max(2 * words.length, wordsRequired);
// Array expansion
words = Arrays.copyOf(words, request);
// Because the capacity has been expanded, the length of the bit table to be marked is not user-defined
sizeIsSticky = false;
}
}
// Gets the status of the bits of the specified logical index
public boolean get(int bitIndex) {
// Bit logical index must be greater than or equal to 0
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
// Invariant identity Assertion Verification
checkInvariants();
// Calculates the index of the words array element
int wordIndex = wordIndex(bitIndex);
// The index of the words array element must be less than the number of words elements in use, and shift 1L left. The bitIndex result is directly combined with the corresponding words element. If not all bits are 0, it returns true, otherwise it returns false
// Similar to this (the scenario that returns true): 0000 1010 & 0000 1000 = > 0000 1000 = > it indicates that the element in the located words has set the bit corresponding to 1L < < bitindex to 1 through the set method
// Similar to this (the scenario that returns false): 0000 0110 & 0000 1000 = > 0000 0000 = > indicates that the element in the located words has not been set through the set method. The bit corresponding to 1L < < bitindex is 1, and the corresponding bit uses the default value of 0
return (wordIndex < wordsInUse) && ((words[wordIndex] & (1L << bitIndex)) != 0);
}
// Sets the bit of the specified logical index to false
public void clear(int bitIndex) {
// Bit logical index must be greater than or equal to 0
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
// Calculates the index of the words array element
int wordIndex = wordIndex(bitIndex);
// If the index of the words array element is greater than or equal to the number of words elements being used, it indicates that the bits of the logical subscript are in the initialization state and have not been used and do not need to be processed
if (wordIndex >= wordsInUse)
return;
// Equivalent to words [wordindex] = words [wordindex] & (~ (1L < < bitindex))
// Invert the bits of the left shift result, and then perform and operation with the corresponding words element, and then re assign the value to the corresponding words element
// Similar to: 0000 1100 & (~ (0000 1000)) = > 0000 1100 & 1111 0111 = > 0000 0100
words[wordIndex] &= ~(1L << bitIndex);
// Recalculate the value of wordsInUse, that is, refresh the calculated value of the used words element
recalculateWordsInUse();
// Invariant identity Assertion Verification
checkInvariants();
}
Let's simulate the process of the set method:
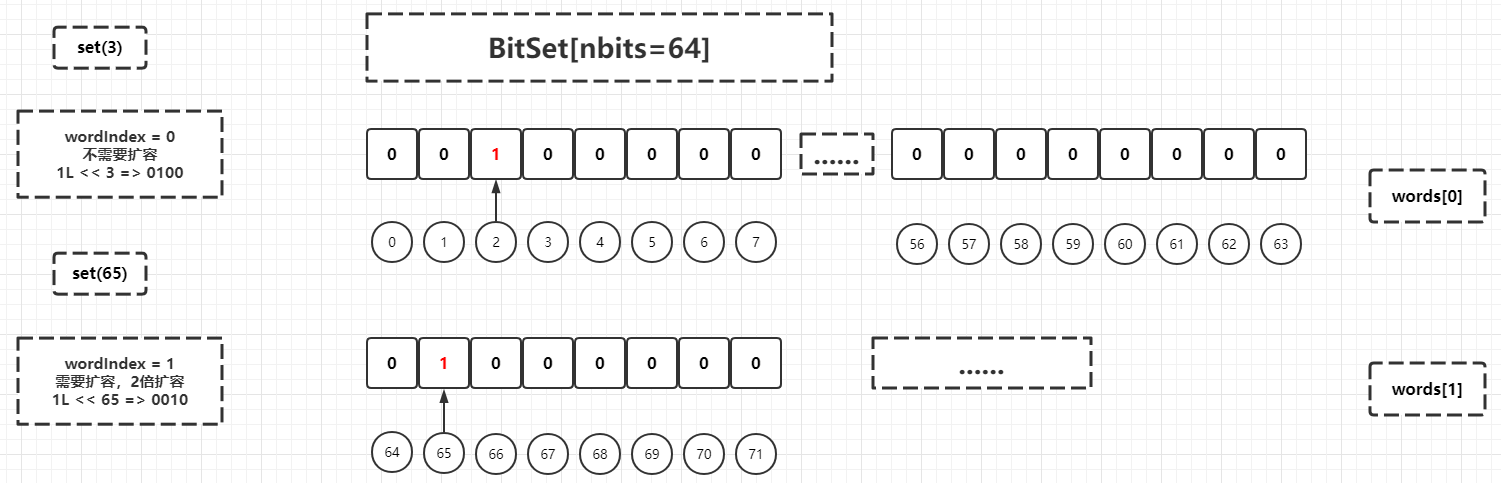
Next, let's look at the methods related to set operation:
// Judge whether there is an intersection between two bitsets. This is a judgment method and will not modify the structure of the current BitSet
public boolean intersects(BitSet set) {
// Compare the number of words elements used by the current BitSet instance and the input BitSet instance, and take the smaller value as the traversal benchmark
for (int i = Math.min(wordsInUse, set.wordsInUse) - 1; i >= 0; i--)
// Traverse and compare the elements of each word array, and return true as long as the operation result is not 0 (this condition is very loose, as long as the bits of two BitSet instances in the same logical index in the underlying logical bit table are 1)
if ((words[i] & set.words[i]) != 0)
return true;
return false;
}
// AND operation. The bottom layer is the words array element corresponding to the index of two BitSet instances. Intuitively, it is to calculate the intersection of two BitSet instances AND store them in this BitSet instance
public void and(BitSet set) {
// The input parameter is this BitSet instance and will not be processed
if (this == set)
return;
// If the current BitSet instance has used more words array elements than it has passed in, the current BitSet instance sets the extra words array elements to 0
while (wordsInUse > set.wordsInUse)
words[--wordsInUse] = 0;
// Traverse the used elements of the words array of the current BitSet instance, and perform and operation and re assignment with the same index elements of the incoming BitSet instance
for (int i = 0; i < wordsInUse; i++)
words[i] &= set.words[i];
// Recalculate the value of wordsInUse, that is, refresh the calculated value of the used words element
recalculateWordsInUse();
// Invariant identity Assertion Verification
checkInvariants();
}
// OR operation, the bottom layer is to perform OR operation on the words array elements of the corresponding indexes of the two BitSet instances. Intuitively, it is to calculate the union of the two BitSet instances and store them in this BitSet instance
public void or(BitSet set) {
// The input parameter is this BitSet instance and will not be processed
if (this == set)
return;
// Calculate the common part of the used elements of the words Array in the two bitsets, which is actually the smaller wordsInUse
int wordsInCommon = Math.min(wordsInUse, set.wordsInUse);
// The number of elements used in the words array of the current BitSet instance is smaller than that of the incoming BitSet instance. Expand the capacity based on the incoming instance, and copy its wordsInUse value
if (wordsInUse < set.wordsInUse) {
ensureCapacity(set.wordsInUse);
wordsInUse = set.wordsInUse;
}
// The common parts of the used elements of the two BitSet instance words arrays are or calculated according to the index respectively, and the value is assigned to the words element of the corresponding index of the current BitSet instance
for (int i = 0; i < wordsInCommon; i++)
words[i] |= set.words[i];
// If the incoming BitSet instance has a public part that exceeds the used elements of the words array, this part of the words array elements will also be copied to the current BitSet instance, because there is a capacity expansion judgment before. Here, the wordsInUse of the current BitSet instance is greater than or equal to the wordsInUse of the incoming BitSet instance
if (wordsInCommon < set.wordsInUse)
System.arraycopy(set.words, wordsInCommon,
words, wordsInCommon,
wordsInUse - wordsInCommon);
// Invariant identity Assertion Verification
checkInvariants();
}
// For XOR operation, the bottom layer is that two BitSet instances perform XOR operation on the words array elements corresponding to the index. The implementation is basically similar to OR. After processing, the wordsInUse value of the current BitSet instance needs to be recalculated
public void xor(BitSet set) {
int wordsInCommon = Math.min(wordsInUse, set.wordsInUse);
if (wordsInUse < set.wordsInUse) {
ensureCapacity(set.wordsInUse);
wordsInUse = set.wordsInUse;
}
// Perform logical XOR on words in common
for (int i = 0; i < wordsInCommon; i++)
words[i] ^= set.words[i];
// Copy any remaining words
if (wordsInCommon < set.wordsInUse)
System.arraycopy(set.words, wordsInCommon,
words, wordsInCommon,
set.wordsInUse - wordsInCommon);
recalculateWordsInUse();
checkInvariants();
}
// AND NOT operation: the bottom layer is the words array element of the corresponding index of the two BitSet instances. Before the operation, the words array element of the corresponding index of the BitSet instance is passed into the BitSet instance for non operation. The process is similar to the AND operation
public void andNot(BitSet set) {
// Perform logical (a & !b) on words in common
for (int i = Math.min(wordsInUse, set.wordsInUse) - 1; i >= 0; i--)
words[i] &= ~set.words[i];
recalculateWordsInUse();
checkInvariants();
}
Here, the process of and method is simulated:
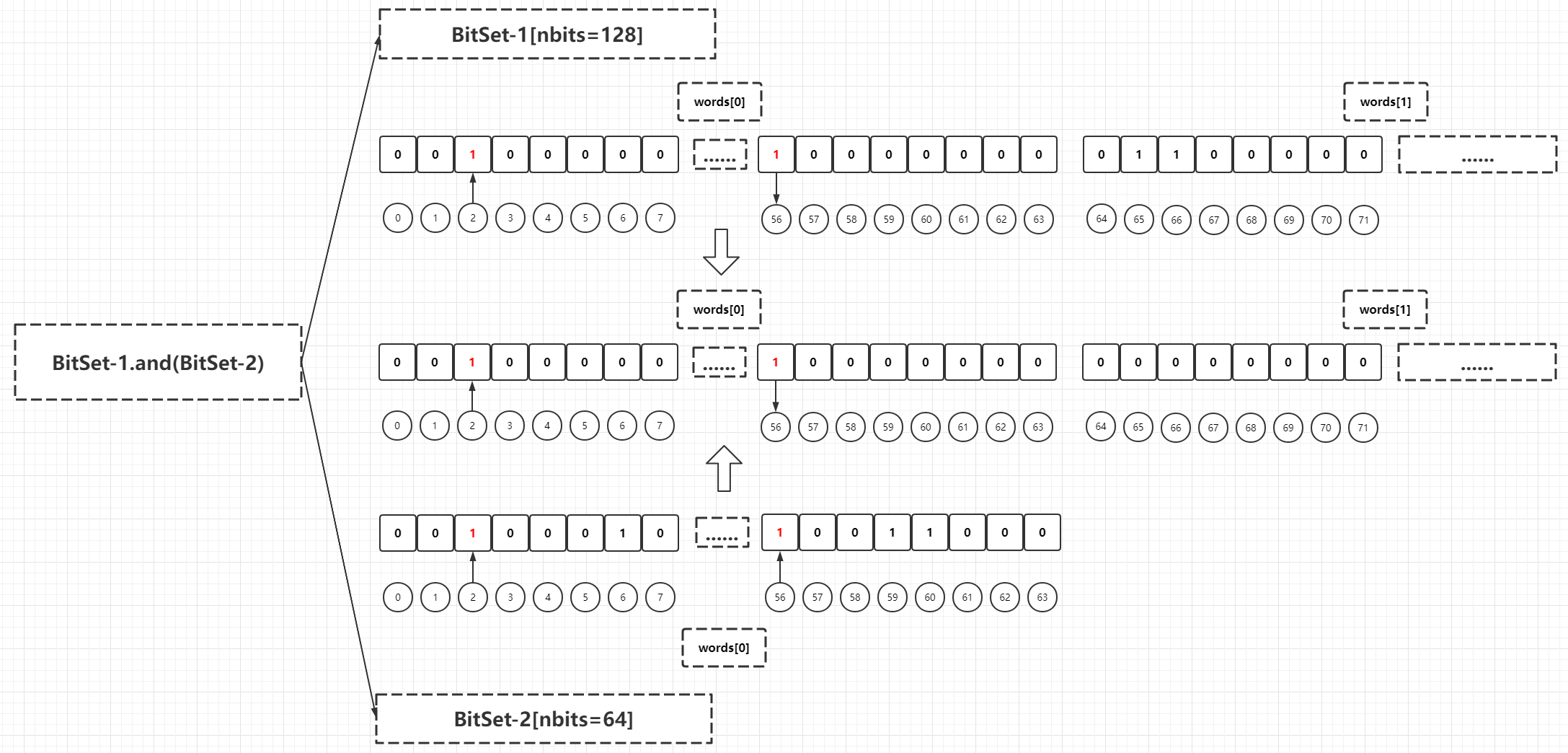
Next, look at the search related methods (nextxxbit, previousYYYBit). Here, take the nextSetBit(int fromIndex) method as an example:
// Starting from the bit logical index fromIndex, search backward and return the logical index of the first bit in true status. If the search fails, return - 1
public int nextSetBit(int fromIndex) {
// The starting bit logical index must be greater than or equal to 0
if (fromIndex < 0)
throw new IndexOutOfBoundsException("fromIndex < 0: " + fromIndex);
// Invariant identity Assertion Verification
checkInvariants();
// Calculate the index of words array elements based on the initial bit logical index
int u = wordIndex(fromIndex);
// The index of the words array element exceeds the number of used words array elements, indicating that the array is out of bounds, and - 1 is returned directly
if (u >= wordsInUse)
return -1;
// This is similar to the left shift of the previous set method, but - 1L is used for the left shift, for example - 1L < < 2 = > 1111 1111 < < 2 = > 1111 1100 (here, it is assumed that the limit length is 8 and the overflow high bit is discarded)
// For example: 0000 1010 & (1111 1111 < < 2) = > 0000 1010 & 1111 1100 = > 0000 1000 (the index value is 4. At present, the result with existence bit of 1 may not be obtained here)
long word = words[u] & (WORD_MASK << fromIndex);
// Traversal based on the obtained word
while (true) {
// It indicates that there is a bit of 1 in word. Calculate and return the logical index of this bit
if (word != 0)
// Calculate the index of the words array element based on the initial bit logical index * 64 + the number of bits with consecutive low order 0 in word
return (u * BITS_PER_WORD) + Long.numberOfTrailingZeros(word);
// Note: if all bits in word are 0, u needs to be incremented backward, which is equal to wordsInUse. If it is out of bounds, it returns - 1. There are two logics: assignment and judgment
if (++u == wordsInUse)
return -1;
word = words[u];
}
}
The nextSetBit(int fromIndex) method first finds the words array element where the fromIndex is located, and then retrieves it later if it is not satisfied. A classic use example is also given in the annotation of this method. Here is an excerpt:
BitSet bitmap = new BitSet();
// add element to bitmap
// ... bitmap.set(1993);
for (int i = bitmap.nextSetBit(0); i >= 0; i = bitmap.nextSetBit(i + 1)) {
// operate on index i here
if (i == Integer.MAX_VALUE) {
break; // or (i+1) would overflow
}
}
Finally, let's look at some Getter methods related to specification properties:
// Gets the total number of bits in the BitSet
public int size() {
// words array length * 64
return words.length * BITS_PER_WORD;
}
// Gets the total number of bits in the BitSet with a bit value of 1
public int cardinality() {
int sum = 0;
// Get the number of bits with 1 of each used words array element, and then accumulate
for (int i = 0; i < wordsInUse; i++)
sum += Long.bitCount(words[i]);
return sum;
}
// Obtain the logical size of BitSet (not only the initialized but unused high-order bits), which is simply the logical index with the first bit value of 1 after removing the high-order bits from words[wordsInUse - 1], such as 0001 1010, three high-order consecutive zeros, and the logical index is 4
public int length() {
if (wordsInUse == 0)
return 0;
return BITS_PER_WORD * (wordsInUse - 1) +
(BITS_PER_WORD - Long.numberOfLeadingZeros(words[wordsInUse - 1]));
}
Other methods such as setting or clearing values according to the range, such as set(int fromIndex, int toIndex), clear(int fromIndex, int toIndex), are limited to space and do not conduct detailed analysis. The routine is roughly similar.
Problems not solved by BitSet
ADDRESS_ BITS_ PER_ The choice of word size is determined purely by performance considerations is also mentioned in the field notes of word. The basic addressing value 6 here is selected because the long array is selected at the bottom layer to reduce the expansion times of the bottom array as much as possible. However, there is a contradictory problem here. It seems that there is no way to find data types whose bit width is larger than long and occupy memory space equivalent to long in JDK. For example, byte and String (the bottom layer is char array) will far exceed long in capacity expansion times. Because the bottom layer is an array storage structure and does not limit the lower and upper boundaries of the elements in the array, too much useless memory space will be wasted in some specific scenarios. By modifying the example mentioned above, if you want to add all integers between 1 billion and 2 billion to the BitSet instance (these values are marked as 1 in the corresponding logical bit index of BitSet), in the underlying bit table of BitSet instance, the value of logical index [0,1 billion] will be the initialization value 0, that is, about half of the words[N] will be 0, This part of memory space is completely wasted. In the actual business scenario, most of the time, the business primary key does not use the self increasing primary key of the database, but uses the numerical primary key with self increasing trend generated by algorithms such as snowflag. If the benchmark timestamp defined by the algorithm is relatively large, the generated value will far exceed the upper limit of int type (carried by long type). That is, the problems not solved by BitSet are as follows:
- Question 1: the upper limit of the logical index value of the bit table is integer MAX_ Value, there is no way to expand to long MAX_ Value, because the length attribute of the array in the JDK is of type int, which can be obtained from Java lang.reflect. This limitation is known in the array class. The author believes that this problem cannot be solved from the bottom for the time being
- Problem 2: BitSet does not consider the scenario optimization of the logical index range of the known bit table, that is, the 0 value of [0, lower boundary) must be stored, which will waste too much useless memory space in some specific scenarios
For problem 1, consider making a simple mapping. Suppose [Integer.MAX_VALUE + 1,Integer.MAX_VALUE + 3] need to be stored in BitSet instance, and [1,3] can be actually stored. After processing, use long realindex = (long) bitindex + integer MAX_ Value restores the actual index value, which can logically expand the storage range of BitSet, and guess that it can meet more than 99% of the scenarios:
public class LargeBitSetApp {
public static void main(String[] args) {
long indexOne = Integer.MAX_VALUE + 1L;
long indexTwo = Integer.MAX_VALUE + 2L;
long indexThree = Integer.MAX_VALUE + 3L;
BitSet bitmap = new BitSet(8);
// set(int fromIndex, int toIndex) => [fromIndex,toIndex)
bitmap.set((int) (indexOne - Integer.MIN_VALUE), (int) (indexThree - Integer.MIN_VALUE) + 1);
System.out.printf("Index = %d,value = %s\n", indexOne, bitmap.get((int) (indexOne - Integer.MIN_VALUE)));
System.out.printf("Index = %d,value = %s\n", indexTwo, bitmap.get((int) (indexTwo - Integer.MIN_VALUE)));
System.out.printf("Index = %d,value = %s\n", indexThree, bitmap.get((int) (indexThree - Integer.MIN_VALUE)));
}
}
// Output results
Index = 2147483648,value = true
Index = 2147483649,value = true
Index = 2147483650,value = true
For question 2, there is a ready-made implementation, that is, the class library RoaringBitmap. The warehouse address is: https://github.com/RoaringBitmap/RoaringBitmap . The class library is used by many big data components of Apache and can stand the test of production environment. Import dependencies as follows:
<dependency>
<groupId>org.roaringbitmap</groupId>
<artifactId>RoaringBitmap</artifactId>
<version>0.9.23</version>
</dependency>
Easy to use:
public class RoaringBitmapApp {
public static void main(String[] args) {
RoaringBitmap bitmap = RoaringBitmap.bitmapOf(1, 2, 3, Integer.MAX_VALUE, Integer.MAX_VALUE - 1);
System.out.println(bitmap.contains(Integer.MAX_VALUE));
System.out.println(bitmap.contains(1));
}
}
// Output results
true
true
RoaringBitmap distinguishes different scenarios to establish the underlying storage container:
- Sparse scene: the ArrayContainer container is used, and the number of elements is less than 4096
- Intensive scenario: use BitmapContainer container, similar to Java util. BitSet implementation, the number of elements is greater than 4096
- Aggregation scenario (understood as a mixture of the first two scenarios): use the RunContainer container
Summary
Learning and analyzing the source code of BitSet is to better deal with the operation between a large number of data sets in a limited state in the actual scene. There is a matching scene in the author's business. If there is an opportunity later, it will be expanded in detail in another practical article.
reference material:
- JDK11 related source code
- RoaringBitmap Performance Tricks
(end of this paper c-4-d e-a-20220103)