Problem description

There is an N x N square. Each square has some gold coins. You can get the gold coins as long as you stand in the square. You stand in the top left corner of the grid, and you can walk from one grid to its right or lower grid at a time. How can I get the most gold coins.

Input format

On the first line, enter a positive integer n.
The following n lines describe the grid. The number of gold coins is guaranteed to be a positive integer not exceeding 1000.

Output format

The maximum number of gold coins you can take.

sample input

3
1 3 3
2 2 2
3 1 2

sample output

11

I am a newcomer to the algorithm. I was learning dynamic programming two days ago. When I was writing a topic on the official website of the Blue Bridge Cup today, I found a relatively simple and new topic with few solutions. Therefore, I made this article as a note. I hope this article can be helpful to readers.

As the meaning of the title shows, the author believes that this is an upgraded version of the recursive basic problem "walking the maze", but on this basis, additional gold coins are added, which means that a path is needed to maximize the total value of all gold coins on the total path. In that case, we might as well use the recursive method for operation

We need a dp array (in fact, the array left by the previous question is too lazy to change its name) to store the gold coins of the map, a variable n to store the size of the array, and a dp1 array to store the dynamic planning

First of all, since there is an operation on the value, we must return the int type (as shown in the title). We write the int type function to solve the title

Let's put int walk (int *dp,i,j) aside first. In the main function, we initialize the map first and initialize it at the same time

Then directly output the value returned by walk. Let's write the walk function later.

int main()
{
    cin >> n;
    for (int i = 0;i < n;i++)
    {
        for (int j = 0;j < n;j++)
        {
            cin >> dp[i][j];            
        }
    }
    cout << walk(dp,0,0);
}

The title says to go to the lower right corner, only the operation from down to right. Take i and j as an example, 0 and 0 are the upper left corner

When we call the walk function, there are three cases

1. If the coordinate has exceeded our predetermined range, we will directly return 0 to terminate the recursion

2. The coordinate is within the predetermined range

Here, I quote Mr. Hao Bin's understanding of recursion. I think it is very helpful to solve such problems

"Solving the problem with scale N requires the solution of the problem with scale N-1"

When we are at 0,0, there are only two operations. Go down and go down. No matter what the final result is, a value will always be returned to us. Therefore, combined with the above, we have the following code

int walk(int dp[1000][1000],int i,int j)
{
    if (i >= n - 1 && j >= n - 1)
    {
        return dp[n-1][n-1];  //If it's over
    }
    else
    {   
        if (i <n && j < n) //If within the predetermined range
        {
            int r1 = dp[i][j] + walk(dp, i , j+1); //J is left and right, and j+1 is right
            int r2= dp[i][j] + walk(dp, i+1,j);//i is up and down, i+1 is down
            return max(r1, r2);//Returns the maximum value in both cases
        }
        else
        {
            return 0; //If you go out
        }
    }
}

The principle is: if you need to know how to get the maximum benefit from 0,0 to the end, you need to know the maximum benefit scheme from 0,0 + 1 and 0 + 1,0 to the end. With this recursion, the scale of the final question decreases from N to 1. At this time, all elements are out of the stack, and the answer comes out

After submitting to the Blue Bridge Cup training system, the author thought he could answer correctly, but only got 10 points. After checking, it was found that it was a timeout problem

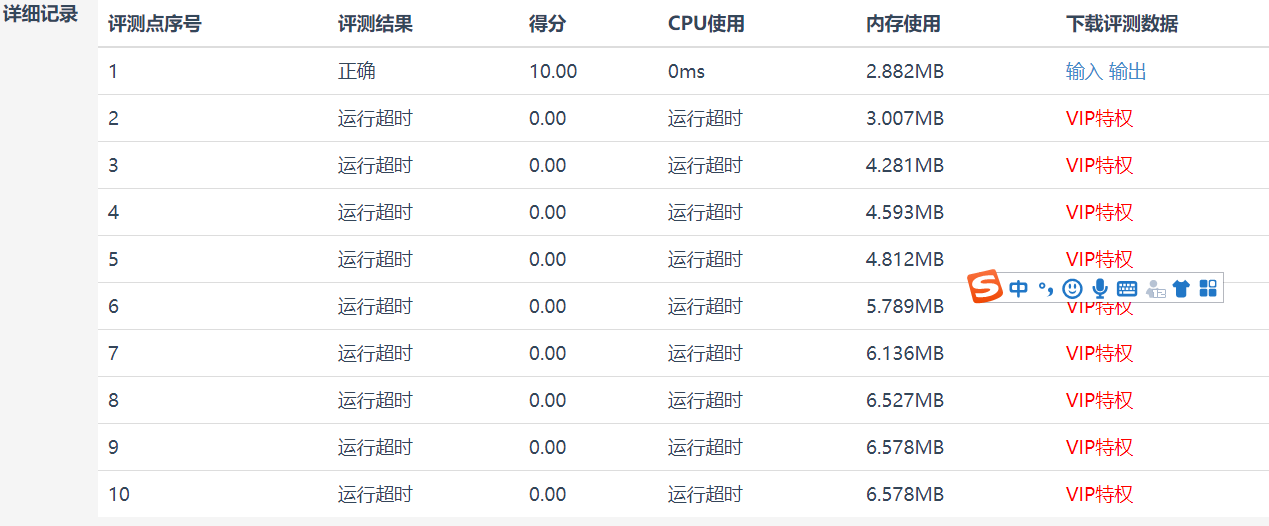
When I suddenly thought of learning the basis of dynamic programming, the online teacher said: sometimes dynamic programming is to reduce and omit the repeated work of some recursive problems. I looked at the code and found a problem: we are divided into two ways, right or down, and down and right have new right and new left, left and right superposition, The path of a module must be repeatedly calculated and accessed

For example: 1 2 3

               4 5 6

               7 8 9

When shunting to 2 and 4, the elements accessed from 2 down and 4 to the right are the same, which means that during this period, we repeatedly visit. The lower we go, the number of repeated visits increases exponentially. Therefore, we need to save the path with the help of auxiliary array

Every time you visit a path point, you will judge whether it has been accessed. If yes, you can directly access the optimal solution under the path. If not, you can calculate the optimal solution of the path point and throw it into the auxiliary array

Finally passed, the worst time is 0.5s

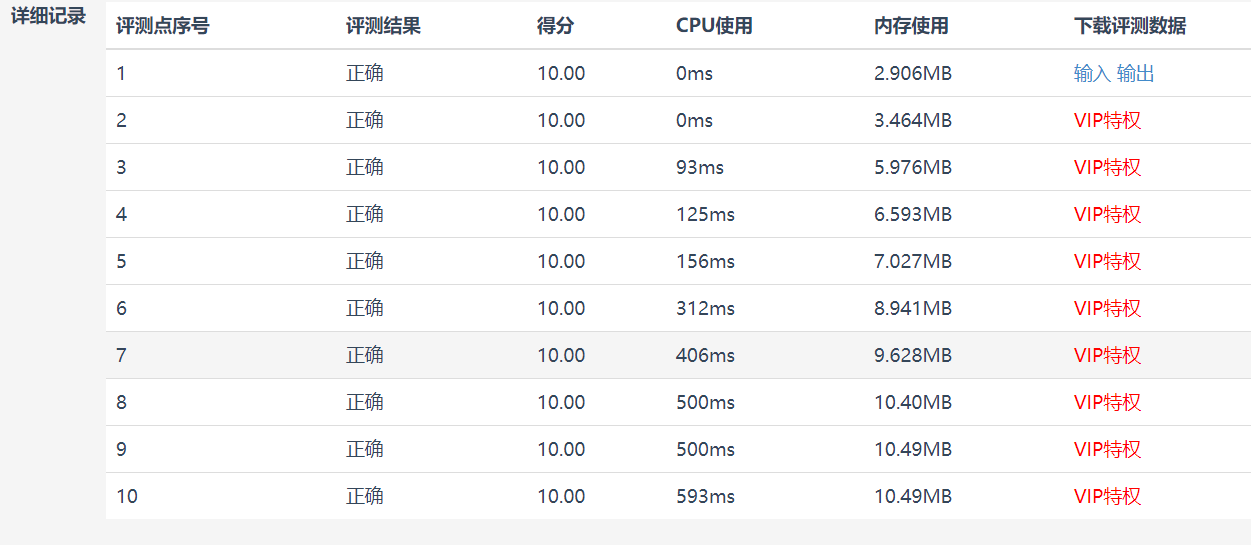
The author consulted CSDN and other forums on the solution of this problem. Few people use the recursive method. Most of them establish dp array, use the double-layer for loop to fill in the dp array, and finally output it directly. I picked a relatively simple code and ran the Blue Bridge Cup again. I found that the time is almost the same, and the recursive method is a few milliseconds faster. The principle is basically the same. I think the method in the article is easier to understand.

The final code is as follows:

using namespace std;
int dp[1000][1000];
int dp1[1000][1000];
int n;

int walk(int dp[1000][1000],int i,int j)
{
    if (i >= n - 1 && j >= n - 1)
    {
        return dp[n-1][n-1];  
    }
    else if(dp1[i][j]==-1)//If the location has not been accessed
    {   
        if (i <n && j < n)
        {
            int r1 = dp[i][j] + walk(dp, i , j+1);
            int r2= dp[i][j] + walk(dp, i+1,j);
            dp1[i][j] = max(r1, r2);
            return max(r1, r2);
        }
        else
        {
            return 0;
        }
    }
    else
    {
        return dp1[i][j];
    }
}

int main()
{
    cin >> n;
    for (int i = 0;i < n;i++)
    {
        for (int j = 0;j < n;j++)
        {
            cin >> dp[i][j];
            dp1[i][j] = -1;
        }
    }
    cout << walk(dp,0,0);
}

If there are errors in the program article, please inform the author. Thank you for reading!