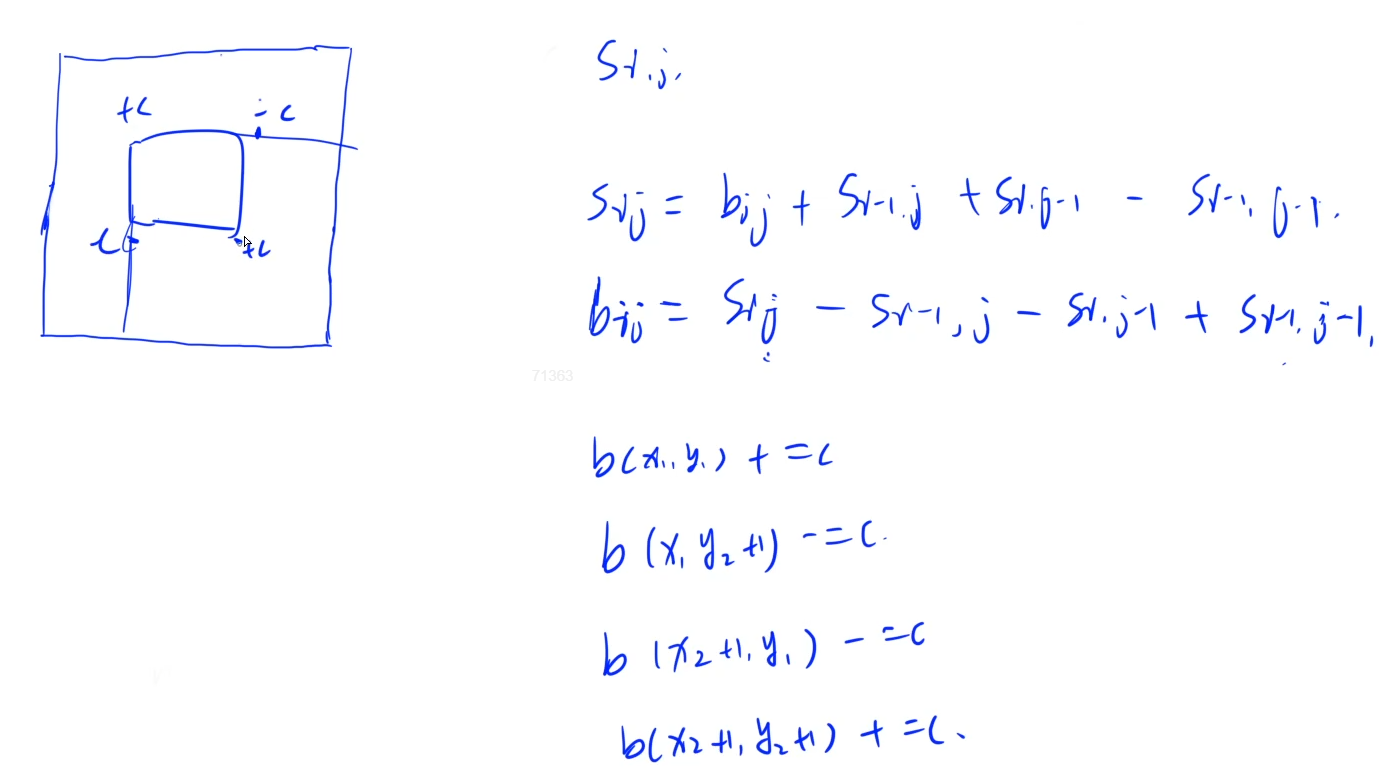1, The index of the tree array starts from 1
Operation O(logn)
- Single point modification: add a number to the number at a certain position
- Interval query: find the sum of a prefix
Offline practice: modification is not supported
Online practice: support modification
principle
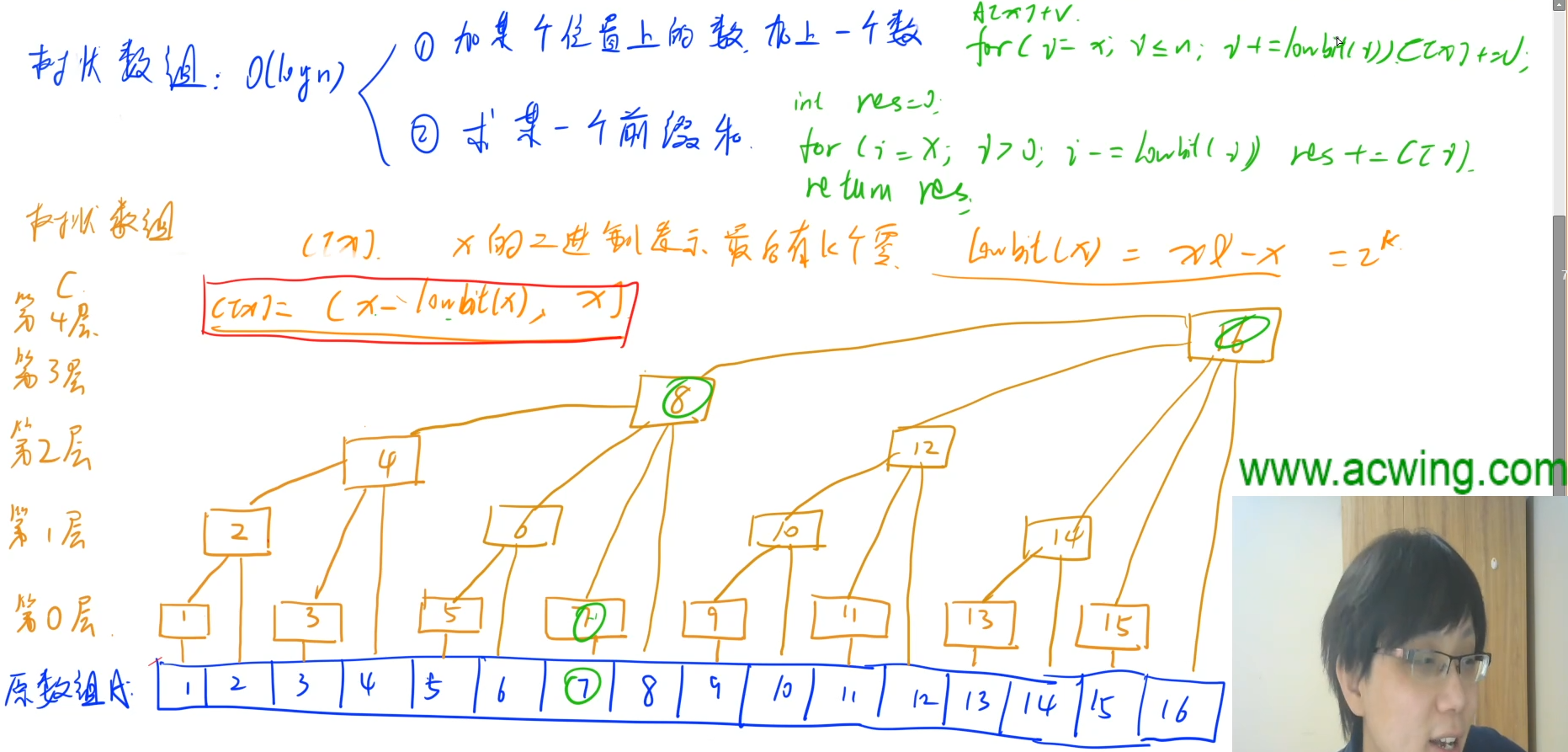
Determination of the number of layers: there are several zeros at the end of the binary representation of x
C [x] = (x-lowbit (x), sum of x]
lowbit(x): returns the value corresponding to the lowest 1 in the binary expression of X
lowbit(6) = 2, because the number corresponding to the lowest bit (the second bit from right to left) in (110) 2 is 21 = 2
1264. Dynamic summation of continuous intervals
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100005;
int a[N],n,m;
int tr[N];//tr[x] represents the sum of (x-lowbit(x),x]
int k,x,y;
int lowbit(int x)
{
return x & -x;
}
void add(int x,int v) //Add a number to the position of x
{
for(int i = x;i <= n;i+=lowbit(i))
{
tr[i] += v;
}
}
int query(int x) //Prefix and of query 1~x
{
int res = 0;
for(int i = x;i>=1;i-=lowbit(i))
{
res += tr[i];
}
return res;
}
int main()
{
scanf("%d%d",&n,&m);
for (int i = 1; i <= n; i ++ ) //Remember to start with subscript 1
{
scanf("%d", &a[i]);
add(i,a[i]);
}
while (m -- )
{
scanf("%d%d%d",&k,&x,&y);
if(k==0)
{
cout<<query(y) - query(x-1)<<endl; //Prefixes and ideas
}
else add(x,y);
}
return 0;
}
1265. Counting stars
Since the number of stars below y is greater than or equal to a certain number of stars in the current ascending order, it is required to count the number of stars below y
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 32005;
int n,x,y;
int tr[N];//Number of stars with x coordinate less than or equal to i
int level[N];//Number of stars at different levels
int lowbit(int x)
{
return x & -x;
}
void add(int t,int x)
{
for(int i=t;i<=N;i+=lowbit(i)) //Note: the range here is [T, n], the value of X will be greater than N, and WA has sent several rounds
{
tr[i] += x;
}
}
int query(int t)
{
int sum = 0;
for(int i=t;i>=1;i-=lowbit(i))
{
sum += tr[i];
}
return sum;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) //Since the coordinates are given in ascending order of y, the coordinates of the current star must be greater than or equal to any previous stars, so statistics should be less than or equal to the current star
//The number of stars x is the number of stars at the lower left
{
scanf("%d%d", &x, &y);
x++;//Mapping x to 1~N+1 makes it easy to use the tree array
level[query(x)]++;
add(x,1);
}
for (int i = 0; i < n; i ++ ) //Note: the range here is 0~n-1, and there can be no stars with level n
{
cout<<level[i]<<endl;
}
return 0;
}
2, Segment tree
Take interval sum as an example
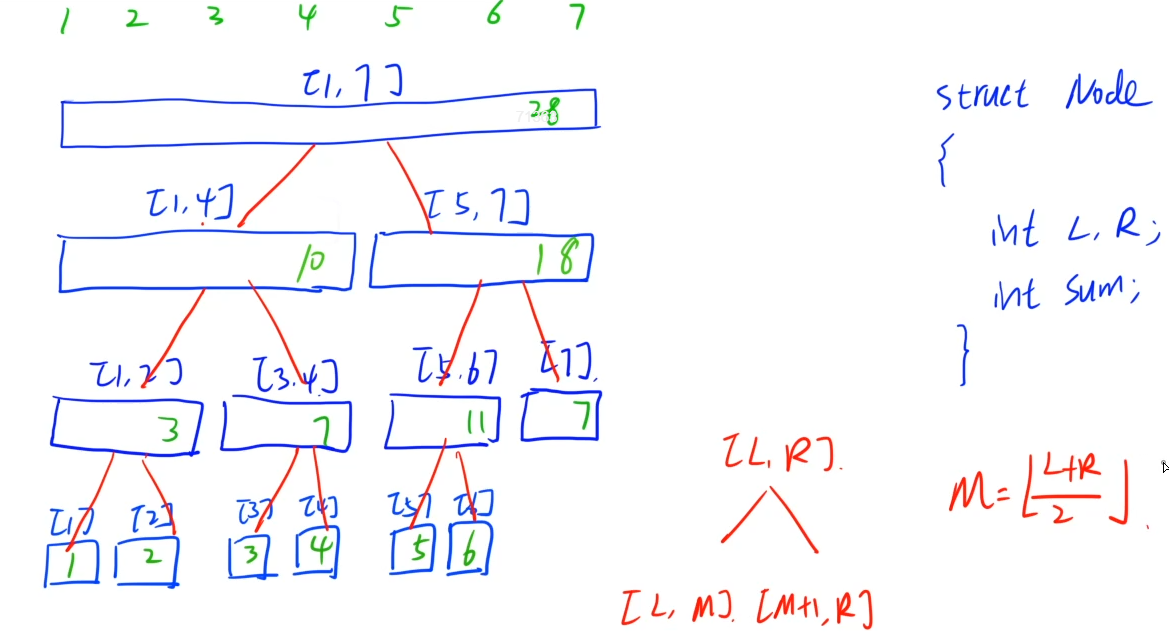
Core operation O(logn)
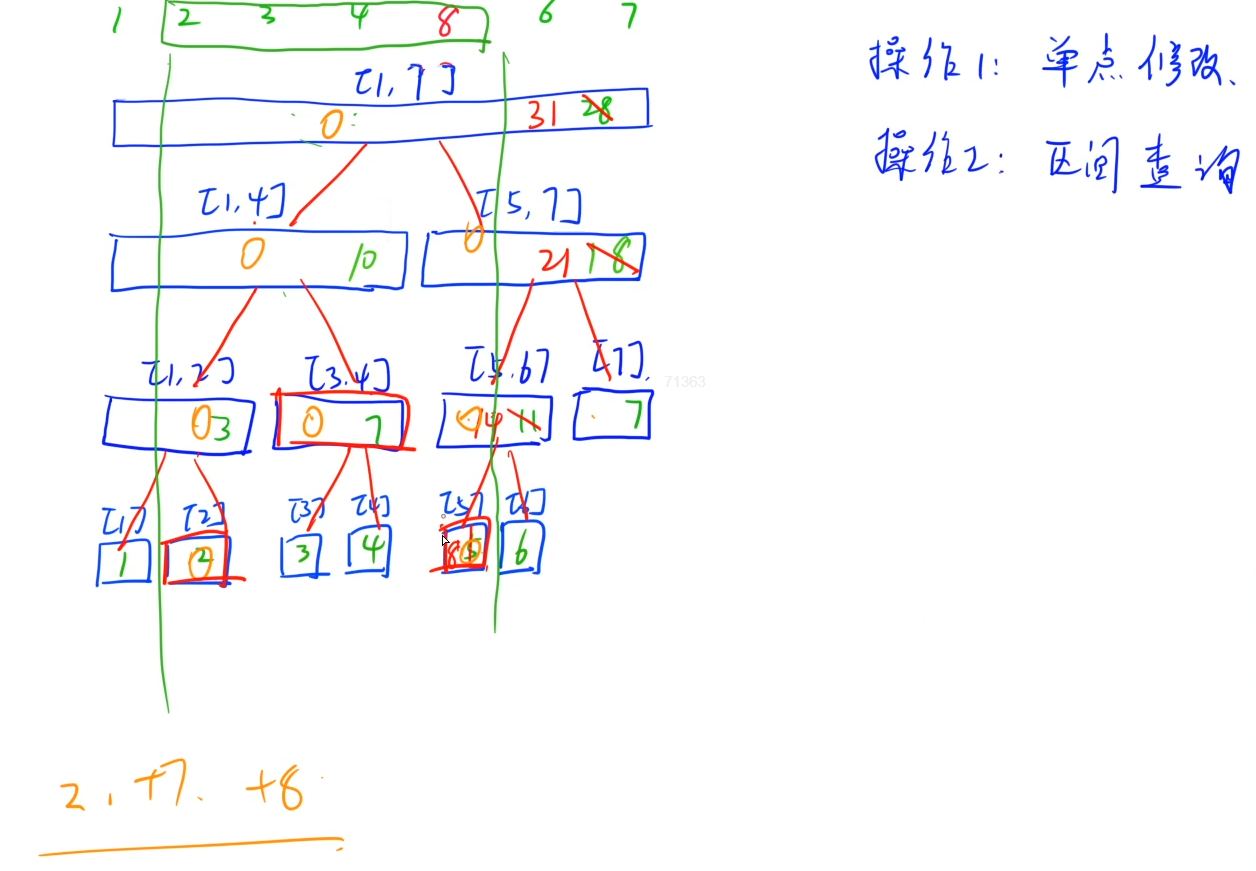
1. Single point modification
Modify recursively. As long as the interval contains the points to be modified, modify the sum of the interval
2. Interval query
Query recursively. As long as the [l,r] of the interval is completely contained by the target interval, it will accumulate and backtrack, otherwise continue to query recursively downward.
Query times less than or equal to 4logn
Main function
Push up updates the current node information with the child node information
build initializes the line segment tree on a section
Modify modify
Query query
pushdown lazy flag
1264. Dynamic summation of continuous intervals
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
int n,m,k,a,b;
int w[N];
struct Node
{
int l;
int r;
int sum;
}tr[N*4]; //The maximum number of nodes in the segment tree is 4N
void pushup(int u) //Update the root node information with the left and right child node information
{
tr[u].sum = tr[2*u].sum + tr[2*u+1].sum;
}
void build(int u,int l,int r) //Formal parameter interpretation: u represents the root node, l and R represent the left and right endpoints of the original data interval
{
if(l==r) tr[u] = {l,r,w[r]};//The number of interval elements is 1. It is a leaf node. It is returned by direct assignment
else
{
tr[u] = {l,r};//Note: initial value must be assigned here
int mid = l+r>>1;
build(u*2,l,mid),build(u*2+1,mid+1,r);//Recursively establish left and right intervals
pushup(u);//Don't forget to update the sum value of the root node and pass the information up
}
}
int query(int u,int l,int r)//Formal parameter interpretation: u represents the root node, l and R represent the left and right endpoints of the target interval
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum; //If the current interval is completely included by the target interval, the current interval sum is returned
int mid = tr[u].l+tr[u].r>>1;
int sum = 0;
if(l <= mid) sum += query(u*2,l,r); //If the left boundary of the target interval is ≤ mid, it indicates that there is an intersection with the left half
if(r > mid) sum += query(u*2+1,l,r);//If the right boundary of the target interval is > mid, it indicates that there is an intersection with the right half
return sum;
}
void modify(int u,int x,int v) //Formal parameter interpretation: u represents the root node, x represents the element subscript, and v represents the value to be added
{
if(tr[u].l == tr[u].r) //If you go to the leaf node, it means that you have found the position in the x corresponding tree and can modify it directly
{
tr[u].sum += v;
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u*2,x,v);//If there is an intersection with the left half, modify it on the left half
else modify(u*2+1,x,v);//If there is an intersection with the right half, modify it on the right half
pushup(u);//Note: finally, you must update the root node information with the son node information
}
}
int main()
{
scanf("%d%d", &n,&m);
for(int i = 1;i<=n;i++)
{
scanf("%d", &w[i]);
}
build(1,1,n);
while (m -- )
{
scanf("%d%d%d",&k,&a,&b);
if(k==0)
{
cout<<query(1,a,b)<<endl;
}
else modify(1,a,b);
}
return 0;
}
1270. Maximum value of sequence interval
#include <iostream>
#include <cstring>
#include <algorithm>
#include <climits>
using namespace std;
const int N = 1e5 + 10;
int w[N];
int n,m,x,y;
struct Node
{
int l;
int r;
int Max;
}tr[N*4];
inline void build(int u,int l,int r)
{
if(l==r) tr[u] = {l,r,w[r]};
else
{
tr[u] = {l,r};
int mid = l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
tr[u].Max = max(tr[u<<1].Max,tr[u<<1|1].Max);
}
}
inline int query(int u,int l,int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u].Max;
int Max = INT_MIN;
int mid = tr[u].l + tr[u].r>>1;
if(l <= mid) Max = max(Max,query(u<<1,l,r));
if(r > mid) Max = max(Max,query(u<<1|1,l,r));
return Max;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
{
scanf("%d", &w[i]);
}
build(1,1,n);
while (m -- )
{
scanf("%d%d",&x,&y);
printf("%d\n",query(1,x,y));
}
return 0;
}
3, 2D/3D difference
Two dimensional difference
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1005;
int b[N][N];
int n,m,q;
void insert(int x1,int y1,int x2,int y2,int c) //x2,y2 must be increased by 1
{
b[x1][y1] += c;
b[x2+1][y2+1] += c;
b[x1][y2+1] -= c;
b[x2+1][y1] -= c;
}
int main()
{
scanf("%d%d%d", &n, &m,&q);
int c;
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
{
scanf("%d", &c);
insert(i,j,i,j,c);
}
}
while (q -- )
{
int x1,y1,x2,y2;
scanf("%d%d%d%d%d", &x1, &y1,&x2,&y2,&c);
insert(x1,y1,x2,y2,c);
}
for (int i = 1; i <= n; i ++ )//Find the prefix sum, that is, the difference matrix is transformed into the original matrix
{
for (int j = 1; j <= m; j ++ )
{
b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + b[i][j];
}
}
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
{
printf("%d ",b[i][j]);
}
puts("");
}
return 0;
}
Three dimensional difference
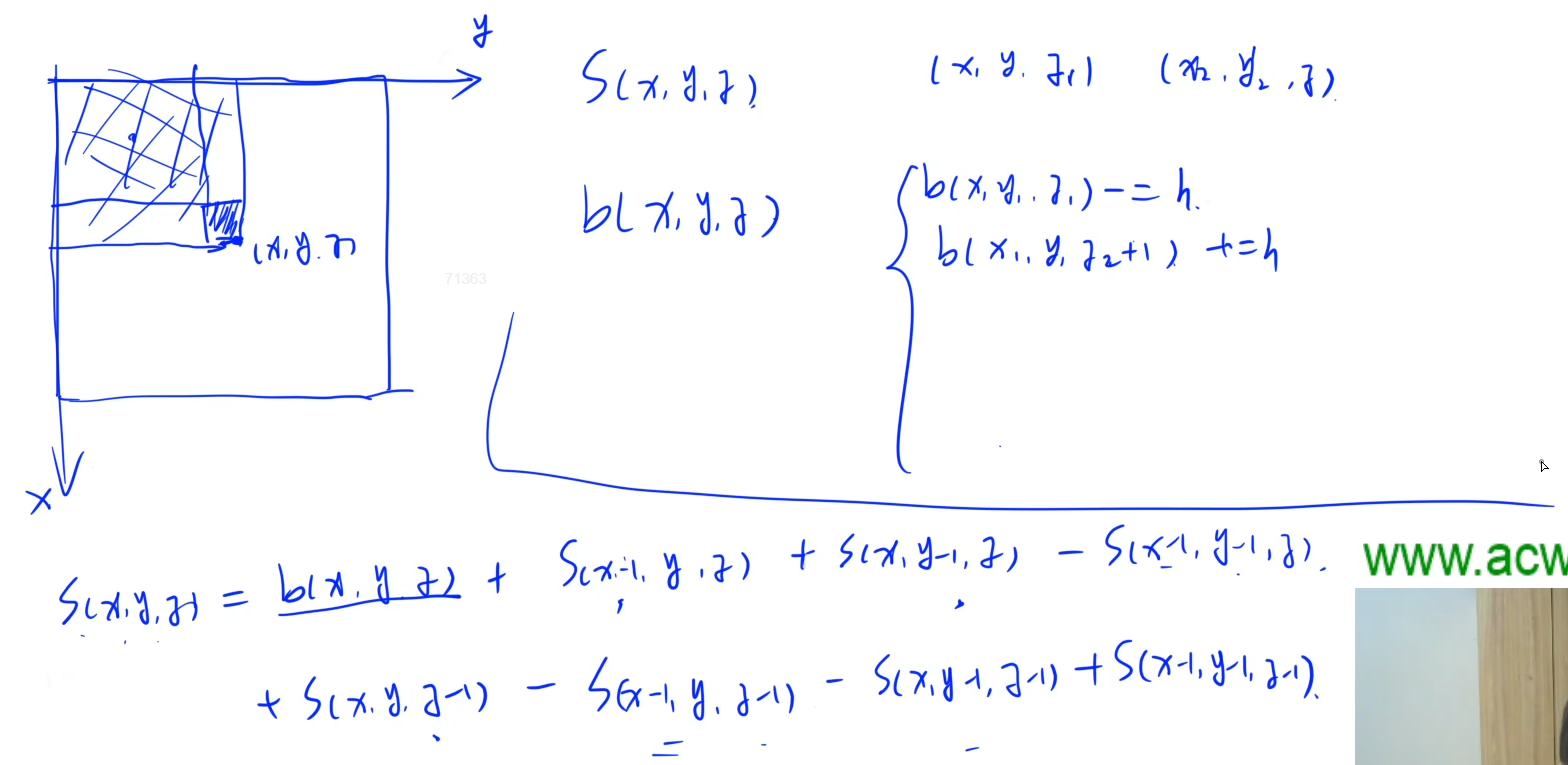
In the formula, for S, the sign of odd minus one is positive and the sign of even minus one is negative
4, Exercises
1215. Children line up
This problem needs to find the number of inverse pairs of each number, and then use the summation formula of the equal difference sequence one by one to calculate the answer. When finding the number of inverse pairs, we need to use the line segment tree
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int h[N],tr[N],n;//The segment tree records the number of each number
int sum[N];
int lowbit(int x)
{
return x & -x;
}
int query(int p)
{
int sum = 0;
for(int i=p;i>=1;i-=lowbit(i))
{
sum += tr[i];
}
return sum;
}
void add(int p,int x)
{
for(int i=p;i<=N;i+=lowbit(i))
{
tr[i]+=x;
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
scanf("%d", &h[i]);
++h[i];//To calculate the prefix and, you need to map to 1~N+1
}
for(int i=0;i < n;i++) //Find out how many numbers in front of each number are larger than it
{
sum[i] += query(N-1) - query(h[i]);
add(h[i],1);
}
memset(tr,0,sizeof tr);//Remember to clear the line segment tree
for (int i = n-1; i >=0 ; i -- )//Find out how many numbers are smaller after each number
{
sum[i] += query(h[i]-1);
add(h[i],1);
}
LL ans = 0;//The answer may explode
for(int i = 0;i<n;i++)
{
//cout<<sum[i]<<" ";
ans += (LL)(1+sum[i])*sum[i]/2;
}
cout << ans<<endl;
return 0;
}
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 10005;
int x1,y1,x2,y2,n;
LL ans;
bool g[N][N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
scanf("%d%d%d%d", &x1, &y1,&x2,&y2);
for(int j=x1;j<x2;j++)
{
for(int k=y1;k<y2;k++)
{
if(!g[j][k])
{
g[j][k] = 1;
++ans;
}
}
}
}
cout << ans << endl;
return 0;
}