Tortoise rabbit race prediction
In other words, there are all kinds of rabbits and turtles in the world, but the research found that all rabbits and turtles have a common characteristic - like running. Therefore, competitions between tortoises and rabbits are constantly taking place in all corners of the world. Xiaohua is very interested in this, so he decided to study the races between different rabbits and tortoises. Once the tortoise and the tortoise have the problem of laziness for more than s seconds, they will find that they are ahead of the tortoise in the race, but they will stop running faster than the tortoise. For different rabbits, the values of t and s are different, but all turtles are the same - they never stop until they reach the end.
However, some races are quite long and it takes a lot of time to watch the whole course. Xiaohua found that as long as he recorded the data of the rabbit and tortoise after the beginning of each race - the speed v1 of the rabbit (which means that the rabbit can run v1 meters per second), the speed v2 of the tortoise, the corresponding T and s values of the rabbit, and the length l of the track - the result of the race can be predicted. Please write a program to predict the result of a game for the input data v1, v2, t, s, l.
Input format
The input has only one line and contains five positive integers v1,v2, t, s and l separated by spaces, where (v1,v2 < = 100; T < = 300; s < = 10; l < = 10000 and is the common multiple of v1 and v2)
Output format
The output consists of two lines. The first line outputs the result of the competition - a capital letter "T" or "R" or "D", indicating that the tortoise wins, the rabbit wins, or both reach the finish line at the same time.
The second line outputs a positive integer, indicating the time (in seconds) spent by the winner (or both sides) to reach the destination.
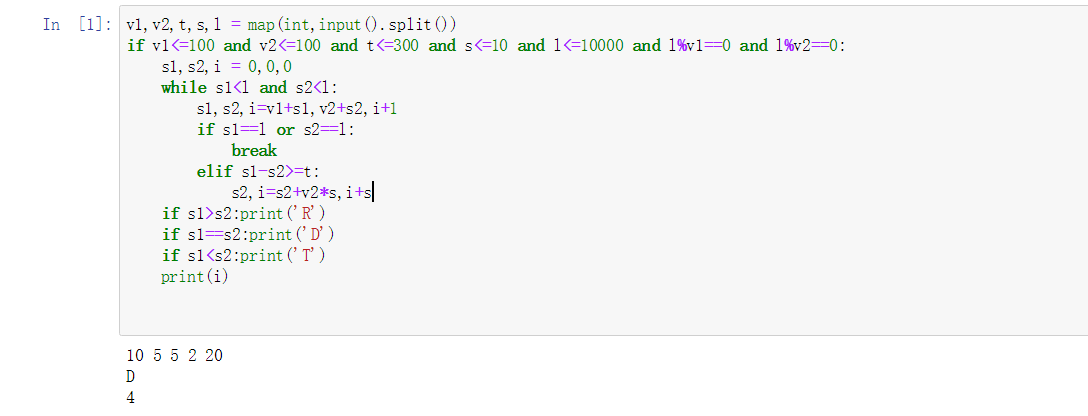
v1,v2,t,s,l = map(int,input().split())
if v1<=100 and v2<=100 and t<=300 and s<=10 and l<=10000 and l%v1==0 and l%v2==0:
s1,s2,i = 0,0,0
while s1<l and s2<l:
s1,s2,i=v1+s1,v2+s2,i+1
if s1==l or s2==l:
break
elif s1-s2>=t:
s2,i=s2+v2*s,i+s
if s1>s2:print('R')
if s1==s2:print('D')
if s1<s2:print('T')
print(i)
Chip test
There are n (2 ≤ n ≤ 20) chips, good and bad. It is known that there are more good chips than bad chips.
Each chip can be used to test other chips. When testing other chips with good chips, the tested chips can be given correctly
Good or bad. When testing other chips with a bad chip, it will randomly give good or bad test results (i.e. this result is consistent with
The actual quality of the tested chip is irrelevant).
Give the test results of all chips and ask which chips are good.
Input format
The first line of the input data is an integer n, indicating the number of chips.
The second row to the n+1 row is a table of n*n, with N data in each row. Each data in the table is 0 or 1, in these n rows
The data in row I and column J (1 ≤ i, j ≤ n) in represents the test results obtained when testing the j-th chip with the i-th chip, 1
It means good, 0 means bad, and it is always 1 when i=j (it does not mean the test result of the chip on itself. The chip cannot be on itself
Test).
Output format
Output the numbers of all good chips from small to large
"""
Understand the problem. If a good chip tests another chip, it is the correct result,
The bad is the random result, which is also said in the title i,j Location means i Chip test j The result of the chip,
So, the second j Columns are other chip tests j As a result, the number of good chips in the title is greater than that of bad chips,
Then let's make statistics j If the number in the column is more than 1 or more than 0, you can judge the quality of the chip"""
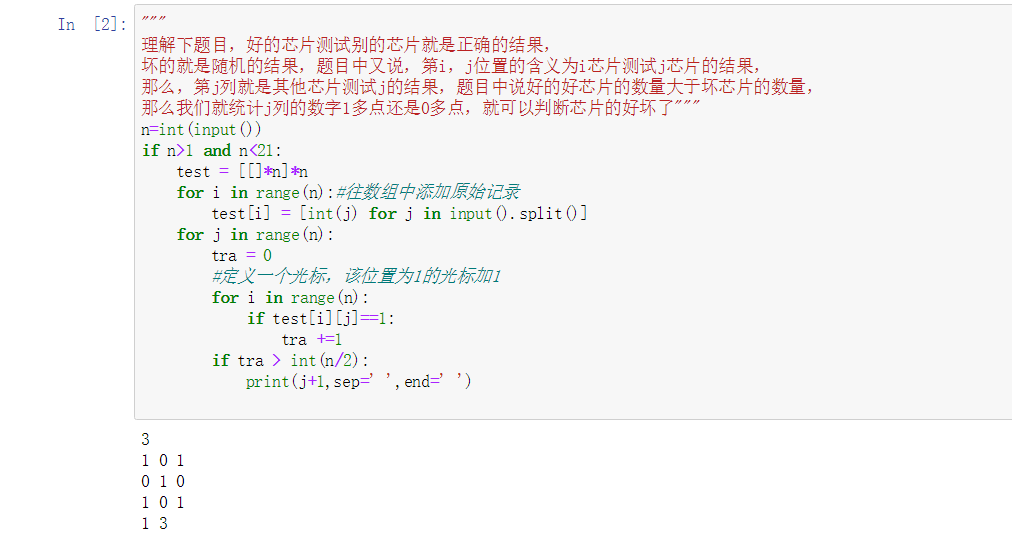
n=int(input())
if n>1 and n<21:
test = [[]*n]*n
for i in range(n):#Add original record to array
test[i] = [int(j) for j in input().split()]
for j in range(n):
tra = 0
#Define a cursor whose position is 1 plus 1
for i in range(n):
if test[i][j]==1:
tra +=1
if tra > int(n/2):
print(j+1,sep=' ',end=' ')
FJ string
Problem description
FJ writes such strings on the sand table:
A1 = "A"
A2 = "ABA"
A3 = "ABACABA"
A4 = "ABACABADABACABA"
... ...
Can you find out the rules and write all the sequences?
Input format
There is only one number: N ≤ 26.
Output format
Please output the corresponding string AN, ending with a newline character. The output must not contain extra spaces or line breaks
Carriage return.
sample input
3
sample output
ABACABA
"""
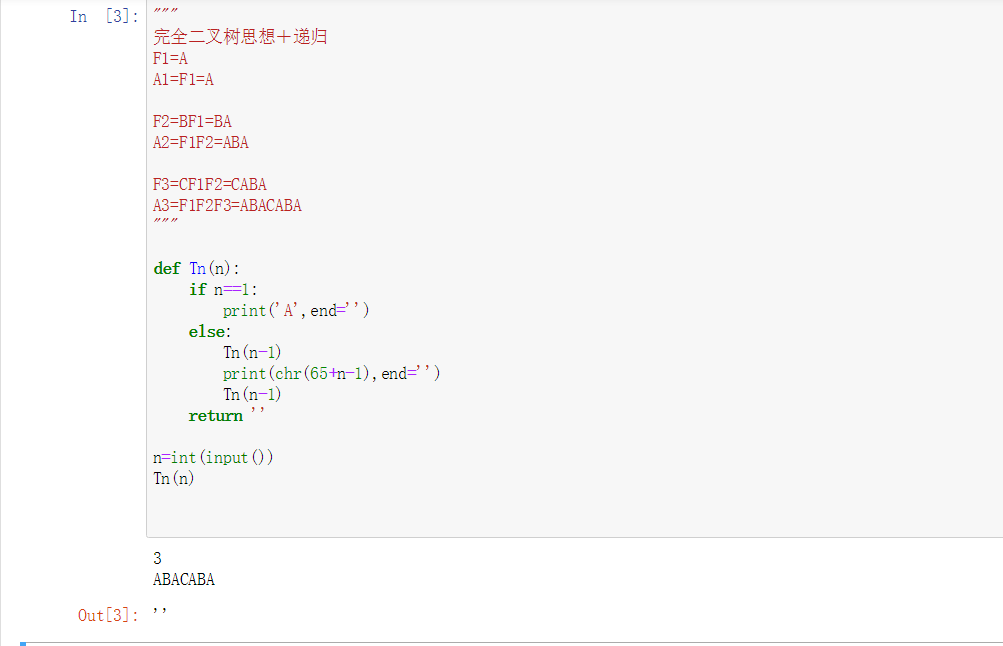
Complete binary tree thought+recursion
F1=A
A1=F1=A
F2=BF1=BA
A2=F1F2=ABA
F3=CF1F2=CABA
A3=F1F2F3=ABACABA
"""
def Tn(n):
if n==1:
print('A',end='')
else:
Tn(n-1)
print(chr(65+n-1),end='')
Tn(n-1)
return ''
n=int(input())
Tn(n)
Dance of Sine
An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
FJ wants cows to calculate the value of Sn. Please help FJ print out the complete expression of SN to facilitate cows to do questions.
Input format
There is only one number: n < 201.
Output format
Please output the corresponding expression Sn, ending with a newline character. The output shall not contain redundant spaces or line breaks or loopbacks
Car symbol.
sample input
3
sample output
((sin(1)+3)sin(1–sin(2))+2)sin(1–sin(2+sin(3)))+1
"""
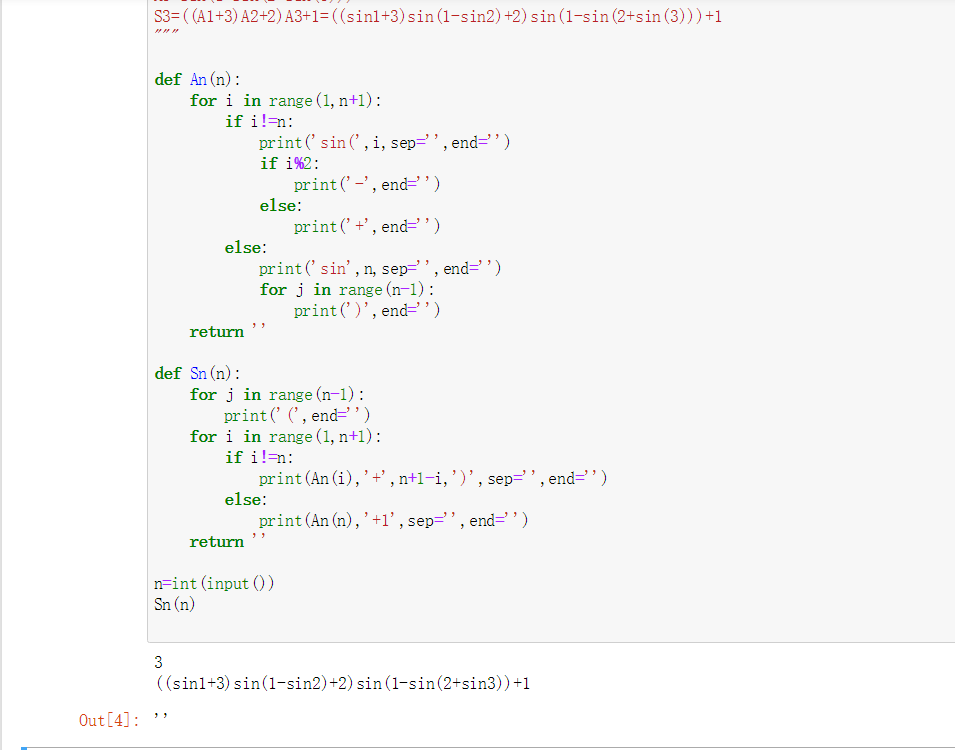
A1=sin1
S1=A1+1=sin1+1
A2=sin(1-sin2)
S2=(A1+2)A2+1=(sin1+2)sin(1-sin2)+1
A3=sin(1-sin(2+sin(3)))
S3=((A1+3)A2+2)A3+1=((sin1+3)sin(1-sin2)+2)sin(1-sin(2+sin(3)))+1
"""
def An(n):
for i in range(1,n+1):
if i!=n:
print('sin(',i,sep='',end='')
if i%2:
print('-',end='')
else:
print('+',end='')
else:
print('sin',n,sep='',end='')
for j in range(n-1):
print(')',end='')
return ''
def Sn(n):
for j in range(n-1):
print('(',end='')
for i in range(1,n+1):
if i!=n:
print(An(i),'+',n+1-i,')',sep='',end='')
else:
print(An(n),'+1',sep='',end='')
return ''
n=int(input())
Sn(n)
Reading method of number