I Year string

Title Linkhttps://www.lanqiao.cn/problems/605/learning/
 

Xiao Ming uses the letter A to correspond to the number 1, B to correspond to 2, and so on, and Z to correspond to 26. For numbers above 27, Xiaoming corresponds with a string of two or more bits, for example, a corresponds to 27, AB corresponds to 28, AZ corresponds to 52 and LQ corresponds to 329.

What is the string corresponding to 2019?

thinking

A~Z correspond to numbers 1 ~ 26 respectively, which is not difficult to understand.

Explain LQ: first take the remainder of 329, and then divide 329. This continues until 329 is 0.

329% 26 = 17, 17 corresponds to Q in the title, and 64 should be added to the computer (the ASCII code corresponding to 64 is @, and 65 corresponds to character A. think about why 64 is added instead of 65 here), 329 / 26 = 12, and 12% 26 = 12. At this time, 12 ＾ corresponds to L.

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])              //Here, the main in parentheses is equivalent to main (), because the variables in parentheses are not used in the main function
{
  // Please enter your code here
  char s[5];
  int sum=2019;int i=0;
  while(sum!=0)
  {
    s[i++]=sum%26+64;
    sum/=26;
  }
  for(int j=i-1;j>=0;j--)                    //Traversal from back
  {
    printf("%c",s[j]);
  }

  return 0;
}

II Sequence evaluation

Title Linkhttps://www.lanqiao.cn/problems/600/learning/

Given the sequence of numbers ， 1, 1, 3, 5, 9, 17,..., starting from item 4 ， each item is the sum of the first 3 ， items.

Find the last 4 # digits of item # 20190324.

thinking

This question is similar to Fibonacci number. You can have a look at the children's shoes you are interested in - > Fibonacci number

One method can use an array a, a1=[1], a2=[1], a3=[1], so each item after the calculation is a[n]=a[n-1]+a[n-2]+a[n-3].

#include<stdio.h>

int main()
{
    
   int a[20190324]={1,1,1};
   for(int i=3;i<20190324;i++)
   {
     a[i]=(a[i-1]+a[i-2]+a[i-3])%10000;    //Because the last four digits need to be taken

   }
   printf("%d",a[20190323]);
}

So will the result of the remainder affect the size of the next number (this is a question that needs to be considered)

The second method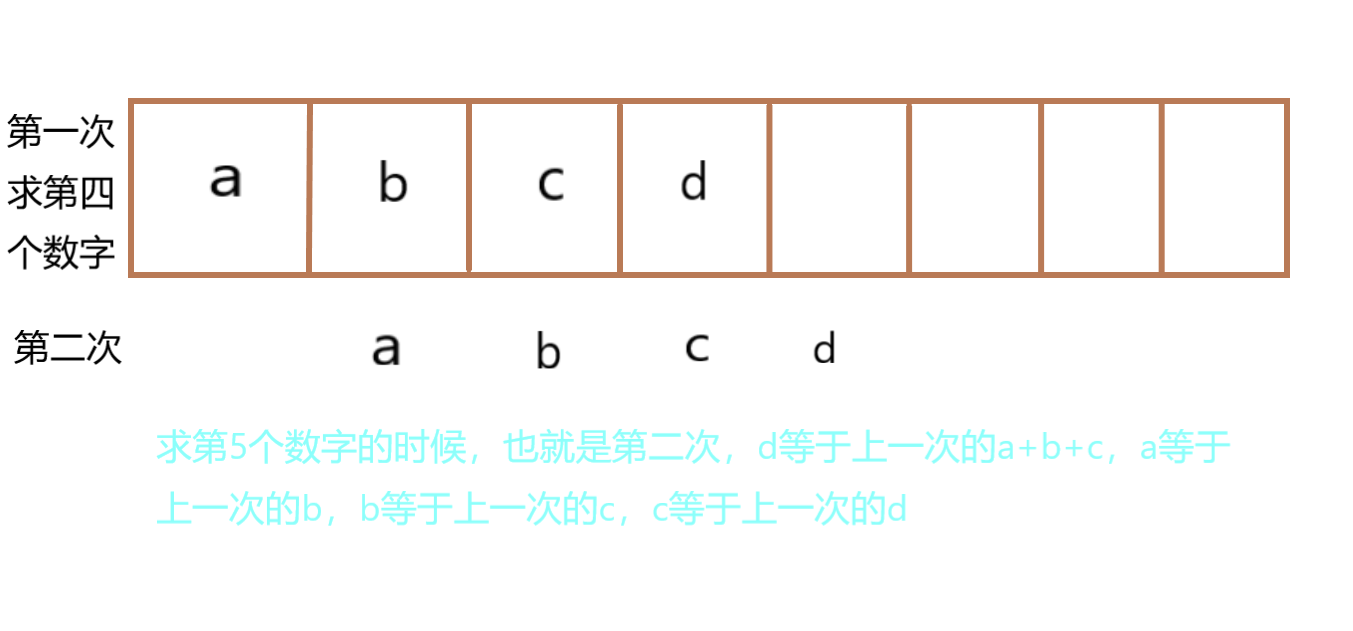

#include<stdio.h>

int main()
{
    
    
    int a = 1, b = 1, c = 1;int d;
    for (int i = 4; i <=20190324; i++)
    {
        d = (a + b + c)%10000;              //Because the title says that it needs the last four digits, so take the remainder of 10000 logarithms
        a = b;
        b = c;
        c = d;
        
    }
  printf("%d",d);
  return 0;
}

III Decomposition of number

Title Linkhttps://www.lanqiao.cn/problems/606/learning/

Decompose 2019 into the sum of 3 # different positive integers, and each positive integer is required to contain no numbers # 2 # and # 4. How many different decomposition methods are there?

Note that the order of exchanging # 3 integers is regarded as the same method, for example, # 1000 + 1001 + 18 and # 1001 + 1000 + 18 are regarded as the same method.

thinking

Let the number take the remainder of 10 and judge whether 2 and 4 appear. The cycle is relatively simple. Look at the following code and pay attention to some details of the notes

#include <stdio.h>
#include <stdlib.h>
#include<stdbool.h>
int judge(int n)            //Judge whether there are 2 and 4
{
  while(n)
  {
    if(n%10==2||n%10==4)return false;
    n/=10;
  }return true;
}


int main()
{
  // Please enter your code here
  int k;
  int cnt=0;
  for(int i=1;i<2019;i++)
  {
    for(int j=1;j<2019;j++)
    {
      k=2019-i-j;
        if(i<j&&j<k&&judge(i)&&judge(j)&&judge(k))    //Note that I < J & & J < K cannot be written as I < J < K
        {
          cnt++;
        }
      
    }
  }
  printf("%d",cnt);
  return 0;
}

IV Sum of special numbers

Title Linkhttps://www.lanqiao.cn/problems/191/learning/

Xiao Ming is very interested in numbers containing 2, 0, 1 and 9 (excluding the leading 0). In the range of 1 to 40, such numbers include 1, 2, 9, 10 to 32, 39 and 40, a total of 28, and their sum is 574.

What is the sum of all such numbers from 1 to n?

Train of thought

Similar to the above question, it is mainly the occurrence of residual judgment 2, 0, 1 and 9

#include <stdio.h>
#include <stdlib.h>
int judge(int n)
{
 while(n)
{
   if(n%10==2||n%10==1||n%10==1||n%10==9||n%10==0)return 1;
   n/=10;
}return 0;
}
int main(int argc, char *argv[])
{
  int cnt=0;
  // Please enter your code here
  int n;
  scanf("%d",&n);
  for(int i=1;i<=n;i++)
  {
     if(judge(i))cnt+=i;       //if(judge(i)) means if judge (I) is not equal to 0
  }
  printf("%d",cnt);
  return 0;
}

if(judge(i)) is equivalent to if (judge (I)= 0)

V Weight of complete binary tree

Title Linkhttps://www.lanqiao.cn/problems/183/learning/ Title Description

Given a complete binary tree containing ＾ N ＾ nodes, each node in the tree has a weight, which is ＾ A1, A2 and ···· AN from top to bottom and from left to right, as shown in the following figure:

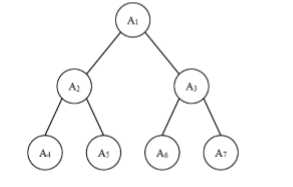
Now Xiao Ming wants to add up the weights of nodes with the same depth. He wants to know which depth has the largest sum of nodes' weights? If the weight sum of multiple depths is the largest, please output the smallest depth.

Note: the depth of the root is 1.

Enter description

The first line contains an integer N (1 < = N<=).

The second line contains N integers A1, A2, ··· AN (-<=N<=).

Output description

Output an integer representing the answer.

Sample input and output

Examples

input

7
1 6 5 4 3 2 1

Output

2

Train of thought

Find the sum of the corresponding numbers of each depth. Here, use a sum array to determine the sum of the corresponding weights of each depth, and then find the maximum value of this array.

Here, k=log(i)/log(2) comes from the following formula

Note: take a look at the third layer A4~A7 and substitute i= 4~7 into the formula respectively. It is found that k is 2;

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
  int temp=0,i,k;
  int ans,max=0,n;
  int sum[100001]={0};
  scanf("%d",&n);
  for(i=1;i<=n;i++)
  {
    scanf("%d",&temp);
    k=log(i)/log(2)+1;        //k represents the depth corresponding to each i
    sum[k]+=temp;
  }
  int deep=log(n)/log(2)+1;  //deep is the depth corresponding to n
  for(i=1;i<=deep;i++)
  {
    if(max<sum[i])
    {
      max=sum[i];
      ans=i;
    }
  }
  printf("%d",ans);return 0;
}

Vi Arithmetic sequence

Title Linkhttps://www.lanqiao.cn/problems/192/learning/

Title Description

The math teacher gave Xiao Ming a problem of summing the arithmetic sequence. But the careless Xiao Ming forgot part of the sequence and only remembered N ， integers.

N ow let's give these # integers. Xiao Ming wants to know how many items are the shortest arithmetic sequence containing these # integers?

Enter description

The first line of input contains an integer N.

The second line contains N integers A1,A2, ····, AN. (note that ∼ A1 ∼ AN ∼ is not necessarily given in the order of the arithmetic sequence)

Where, 2 < = n<= ,  0<=Ai<=.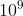

Output description

Output an integer to represent the answer.

Sample input and output

Examples

input

5
2 6 4 10 20

output

10

Example description: the shortest arithmetic sequence containing 2, 6, 4, 10 and 20 is 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20.

Train of thought

Sort first, then find the maximum and minimum values, and find the tolerance (a[n-1]-a[0])/x+1

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
const int maxn=100010;
int cmp(const void*a,const void*b)   //Sort from small to large
{
  return*(int*)a-*(int*)b;
}

int main()
{
    int n,a[maxn];
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
    }

   qsort(a,n,sizeof(int),cmp);       //Sort from small to large
    int x=a[1]-a[0];
    for(int i=1;i<n-1;i++)           //Find minimum value
        x=fmin(x,a[i+1]-a[i]);
    if(x!=0) printf("%d",(a[n-1]-a[0])/x+1);
    else   printf("%d",n);
    return 0;
}