1. Ideas

There are some similarities between BM3D and NLM algorithms. NLM has written before: go to

They all use the features of other regions of the image and the current block features to fuse into denoised image blocks. The main differences are as follows:

        1. Search only within a fixed radius
        2. Stack a limited number of the most similar blocks into a three-dimensional array. First do the 2D orthogonal transformation in the horizontal direction for the image block, and then do the 1D orthogonal transformation in the vertical direction (called Collaborative Filtering)

The first point is to reduce the amount of calculation. Because the noise is spatially independent, it is still necessary to use similar images of other regions to help denoise the current region in the case of a single image

The second point is the key idea: noise still exists after orthogonal transformation. For example, after DCT transformation, the real information of the image is often only distributed in the lower frequency range, while most areas of the high frequency range are often only noise. The method of setting the high frequency noise to zero by threshold can be used to roughly denoise, but it is easy to damage the edge of the image Texture and other high-frequency information, especially in the case of strong noise.

In order to prevent the texture from being hurt by mistake, it is necessary to carry out longitudinal orthogonal transformation to extract the low-frequency components of the same frequency position of similar blocks again. (guess) because it is a similar block, there is a high probability that there are similar real values on the same frequency coordinate. The vertical distribution of these values is also concentrated in the low frequency. After the orthogonal transformation again, the real values are more concentrated, and the noise components still spread throughout the whole range, making the denoising results more accurate and better retaining the original high-frequency components

2. Actual operation

BM3D algorithm is actually an algorithm, which has been done twice, but the second calculation is more simplified and Wiener filtering is introduced. Sometimes it may not be necessary to do a second calculation. This article temporarily discusses the first calculation, and the second one is not finished. Here, for convenience, all orthogonal transforms adopt DCT

Description of algorithm steps:

1. Traverse the picture according to the step size, and for each current block, find a group of similar blocks closest to its pixel value [DCT + Euclidean distance] within the specified radius to form a block set

2. Longitudinal 1D DCT

3. Use a fixed threshold to set the frequency coefficient with lower amplitude to zero and calculate the total number of zero values of the set

4. Do two inverse transformations to restore the whole image block

5. The image block is fused into the denoised image block, and the overlapping part with the leading block outputs the final result by weighted summation

The first step is similar to NLM. Search for similar blocks within a certain range. The judgment conditions of similar blocks are as follows:

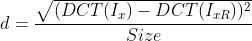
among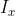Is the current block,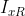Is a reference block

The methods of steps 2, 3 and 4 are relatively simple and will not be described in detail here

Step 5 is mainly introduced to prevent block effect. The weight of each block is determined by the number of non-zero values in its corresponding block set(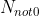), the specific formula is:

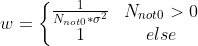
From the perspective of similarity, if the image sets are exactly the same, then after 3D transformation, especially the last 1D transformation, its matrix is very sparse. Because the value of each coordinate is the same in the longitudinal direction, it has only one low-frequency component in the longitudinal direction, so the non-zero value is very small and the weight is higher. On the contrary, if the sets are not similar, the weight is lower

From the perspective of noise, if the more noise components are not set to zero, the more coefficients remain after 3D change and the smaller the weight

Finally, the weight should be multiplied by kaiser window to get the final reduction formula

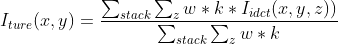
Where stack represents all overlapping blocks, z represents longitudinal coordinates, and k represents two-dimensional kaiser window

Finally, the python implementation is attached:

# -*- coding: utf-8 -*-

import cv2
import numpy as np
import math

def process_bar(percent, start_str='', end_str='', total_length=0):
    bar = ''.join(["\033[31m%s\033[0m"%'   '] * int(percent * total_length)) + ''
    bar = '\r' + start_str + bar.ljust(total_length) + ' {:0>4.1f}%|'.format(percent*100) + end_str
    print(bar, end='', flush=True)

image = cv2.imread('F:/tf_learn--------/impixiv/593.jpg')
image = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)

size = image.shape  # h w c

image = np.array(image/255, dtype=np.float32)
noise = np.random.normal(0, 0.001 ** 0.5, size)
imnoise = image + 1*noise

#cv2.imshow('result',imnoise)
#cv2.waitKey()

sigma = 1 
searchsize = 16 #Image search area radius
blocksize = 4#Image block size
blockstep = 2#Search step
blockmaxnum = 8#Maximum number of similar blocks
searchblocksize = searchsize/blocksize#Number of blocks in radius
kai = np.kaiser(blocksize,5)
kai = np.dot(kai[:,None],kai[None,:])#Two dimensional kaiser

diffT = 100 #Maximum diff allowed to be included in the array
coefT = 0.0005

diffArray = np.zeros(blockmaxnum)#Similar block
similarBoxArray = np.zeros((blocksize,blocksize,blockmaxnum))
#jinbuqu csdn newland


#Make the image size conform to multiple
newh = math.floor((size[0] - blocksize)/blockstep)*blockstep - searchsize
neww = math.floor((size[1] - blocksize)/blockstep)*blockstep - searchsize

newh = math.floor((size[0] - newh - blocksize)/blockstep)*blockstep + newh
neww = math.floor((size[1] - neww - blocksize)/blockstep)*blockstep + neww

imnoise = imnoise[0:newh,0:neww]

#Initialize numerator and denominator
imnum = np.zeros(imnoise.shape)
imden = np.zeros(imnoise.shape)

#Use the upper left corner as the coordinates of the block Each block is denoised independently, as long as we pay attention to the calculation of one block
for y in range(0,newh-blocksize,blockstep): #Check whether it can go to the end completely. Is the scope right
    systart = max(0,y - searchsize)
    syend = min(newh - blocksize,y + searchsize - 1)
    process_bar(y/(newh-blocksize), start_str='speed of progress', end_str="100", total_length=15)
    for x in range(0,neww-blocksize,blockstep):

        sxstart = max(0,x - searchsize)
        sxend = min(neww - blocksize,x + searchsize - 1)
        
        #Sorting matrix initialization
        similarBoxArray[:,:,0] = imnoise[y : y + blocksize,x : x + blocksize]
        hasboxnum = 1
        diffArray[0] = 0
        #Not yourself
        for sy in range(systart,syend,blockstep):
            for sx in range(sxstart,sxend,blockstep):
                if sy == y and sx == x:
                    continue
                
                diff = np.sum(np.abs(imnoise[y : y + blocksize,x : x + blocksize] - imnoise[sy : sy + blocksize,sx : sx + blocksize]))
                
                if diff > diffT:
                    continue
                #Insert
                
                changeid = 0
                if hasboxnum < blockmaxnum - 1:
                    changeid = hasboxnum
                    hasboxnum = hasboxnum + 1
                else:
                    #sort
                    for difid in range(1,blockmaxnum - 1):
                        
                        if diff < diffArray[difid]:
                            changeid = difid
                            
                          
                if changeid !=0:
                    similarBoxArray[:,:,changeid] = imnoise[sy : sy + blocksize,sx : sx + blocksize]
                    diffArray[changeid] = diff
        

        #Start doing dct
        for difid in range(1,hasboxnum):
            similarBoxArray[:,:,difid] = cv2.dct(similarBoxArray[:,:,difid])
        
        #Start 1d, threshold operation and calculate the non-zero number
        notzeronum = 0
        for y1d in range(0,blocksize):
            for x1d in range(0,blocksize):
                temp3ddct =   cv2.dct(similarBoxArray[y1d,x1d,:]) 
                zeroidx = np.abs(temp3ddct)<coefT
                
                temp3ddct[zeroidx] = 0
                notzeronum = notzeronum +temp3ddct[temp3ddct!=0].size
                similarBoxArray[y1d,x1d,:] = cv2.idct(temp3ddct)[:,0]
                
        #jinbuqu csdn newland
        
        if notzeronum < 1:
            notzeronum = 1
            
        #The numerator and denominator used to finally restore the image
        for difid in range(1,hasboxnum):
            #Weight calculation: kaiser * w
            weight = kai /( (sigma ** 2) * notzeronum)
            imidct = cv2.idct(similarBoxArray[:,:,difid])
            
            #Numerator
            imnum[y : y + blocksize,x : x + blocksize] += imidct * weight
            imden[y : y + blocksize,x : x + blocksize] +=  weight
            

        
        x = x + blocksize
    
    y = y + blocksize


#Complete denoising
imout = imnum/imden



cv2.imshow('in',imnoise)
cv2.waitKey(0)
cv2.imshow('out',imout)
cv2.waitKey(0)

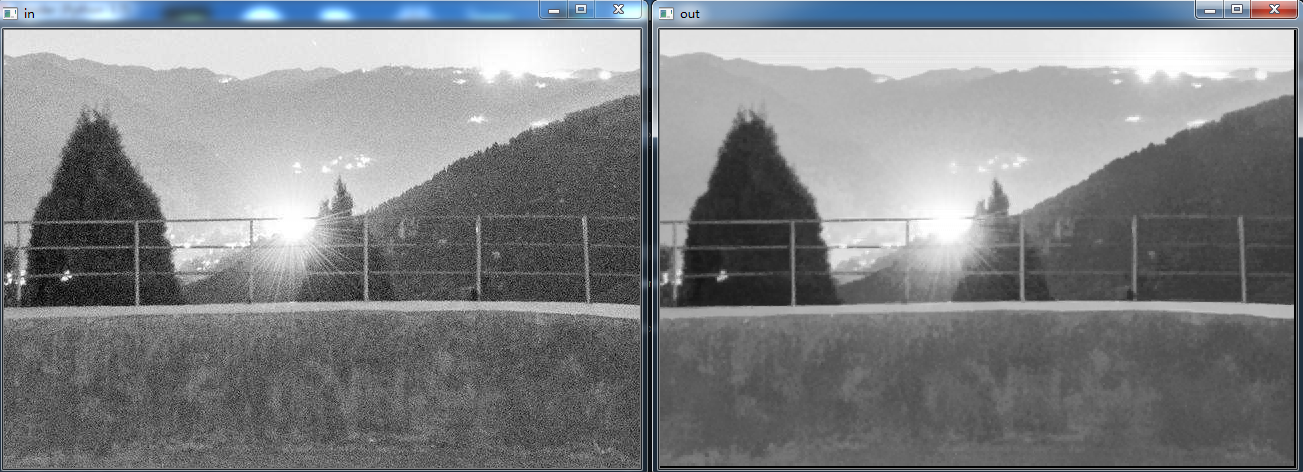
effect: