Branch and bound of algorithm basis (C + + example)
The branch and bound method is similar to the backtracking method, but the backtracking method is to solve all the solutions that meet the constraints in the target, and the branch and bound method is to find a solution that meets the constraints, which is the best.
The so-called "branch" is to use the breadth first strategy to generate all branches (i.e. son nodes) of the extension node in turn.
The so-called "bound" is to calculate the upper bound (or lower bound) of the node in the process of node expansion, and reduce some branches of the search tree while searching, so as to improve the search efficiency.
Some differences between backtracking method and branch and bound method
The backtracking method depth first searches all feasible child nodes of the live node of the stack. After being traversed, it is popped out of the stack to find all solutions that meet the constraints.
Branch and bound method breadth first or minimum consumption first search queue. Each node of the priority queue has only one chance to become a live node to find a solution that meets the constraints or the optimal solution in a specific sense.
Two common branch and bound methods
1) FIFO branch and bound method (breadth first): select the next node as the expansion node according to the queue first in first out principle.
2) Priority queue branch and bound method (minimum loss priority): select the node with the highest priority according to the priority specified in the priority queue to become the current expansion node.
Now let's look at a simplified version of the loading problem: the loading problem of a ship. Is there a reasonable loading scheme to load these n containers on these two ships? Filling the first ship as full as possible is equivalent to selecting a subset of all containers so that the sum of container weights in the subset is closest to the payload.
★ queue branch and bound method
The queue branch and bound method for solving the loading problem only obtains the required optimal value, and then constructs the optimal solution later.
First, check whether the left child node of the current extension node is a feasible node. If so, it is added to the flexible junction queue Q.
Then, the right son node is added to the flexible node queue (the right son node must be a feasible node). After two child nodes are generated, the current extension node is discarded.
In the live node queue, the queue head element is taken out as the current extension node.
The live node queue is empty, the algorithm terminates.
The source code is as follows:
//#include <bits/stdc++.h>
#include <queue>
#include <iostream>
using namespace std;
typedef struct QNode
{
QNode *parent;
int lchild;
int weight;
}QNode;
int n;
int c;
int bestw;
int w[100];
int bestx[100];
void InPut()
{
printf("Number of containers and ship capacity:");
scanf("%d %d", &n, &c);
printf("%d Weight of containers:",n);
for(int i = 1; i <= n; ++i) //I of w[i] starts from 1
scanf("%d", &w[i]);
}
//The reason for qnode * & bestE is that firstly, bestE is an address, secondly, reference is used for assignment, and then used in the for loop
void EnQueue(queue<QNode *> &q, int wt, int i, QNode *E, QNode *&bestE, int ch)
{
if(i == n)
{
if(wt == bestw)
{
bestE = E;
bestx[n] = ch;
return;
}
}
QNode *b;
b = new QNode;
b->weight = wt;
b->lchild = ch;
b->parent = E;
q.push(b);
}
int MaxLoading()
{
queue<QNode *>q;
q.push(0);
int i = 1;
int Ew = 0, r = 0;
bestw = 0;
for(int j = 2; j <= n; ++j)
r += w[j];
QNode *E, *bestE; //The function of best is: after the while loop ends, best points to the leaf node of the optimal solution, and then finds what items are loaded through best - > parent.
E = new QNode; //E here is used as an intermediate quantity to connect parent and child
E = 0; //0 is assigned because the value of the root of the tree is 0. At the beginning of while, it represents root
while(true)
{
int wt = Ew + w[i];
if(wt <= c)
{
if(wt > bestw) //Update bestW in advance and pay attention to the update conditions
bestw = wt;
EnQueue(q, wt, i, E, bestE, 1);
}
if(Ew + r >= bestw) //Right son pruning
{
EnQueue(q, Ew, i, E, bestE, 0);
}
E = q.front();
q.pop();
if(!E) //If the number obtained is 0, it represents the next layer of processing
{
if(q.empty()) //If the queue is empty, the cycle ends
break;
q.push(0); //If there is still data in the queue, it indicates that the cycle has not ended. Add a 0 identifier at the end of the layer
E = q.front();
q.pop();
i++; //Go to the next floor
r -= w[i]; //Calculate the remaining weight
}
Ew = E->weight; //Don't forget to update the value of the latest node
}
for(int j = n - 1; j > 0; --j)
{
bestx[j] = bestE->lchild;
bestE = bestE->parent;
}
}
void OutPut()
{
printf("The optimal loading capacity is %d\n", bestw);
printf("The items loaded are \n");
for(int i = 1; i <= n; ++i)
if(bestx[i] == 1)
printf("%d ", i); // I is the serial number of w[i]; I of w[i] starts from 1
}
int main()
{
InPut();
MaxLoading();
OutPut();
}
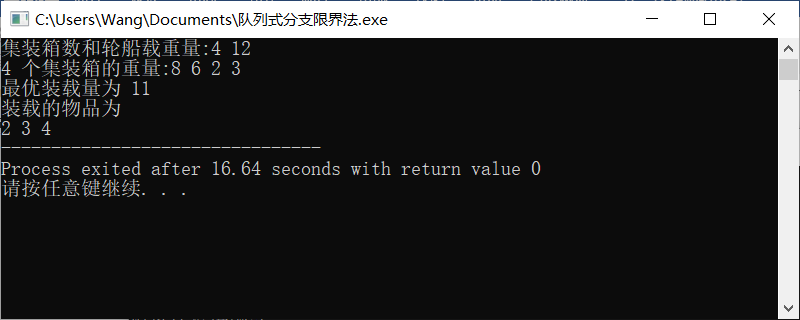
Run as shown in the figure below:
★ priority queue branch and bound method
The priority queue branch and bound method for solving the loading problem uses the maximum priority queue to store the live node table.
The priority of flexible node X in the priority queue is defined as the sum of the corresponding load ew of the path from the root node to node x (i.e. the load ew of the current extended node ship) plus the weight r of the remaining containers (i.e. the upper bound Ew+r is defined as the node priority).
The flexible node with the highest priority in the priority queue becomes the next extension node.
The corresponding payload of the node in the subset tree is the same as its priority (upper bound value), that is, the upper bound value of the leaf node is equal to the weight Ew of the ship at the current leaf node.
In the priority queue branch and bound method, once a leaf node becomes the current expansion node, it can be asserted that the corresponding solution of the leaf node is the optimal solution. The algorithm can be terminated at this time.
The source code is as follows:
//#include <bits/stdc++.h>
#include <queue>
#include <iostream>
using namespace std;
class MaxHeapQNode
{
public:
MaxHeapQNode *parent; //Parent node
int lchild; //Left node: 1; Right node '0'
int weight; //Total weight
int lev; //arrangement
};
struct cmp
{
bool operator()(MaxHeapQNode *&a, MaxHeapQNode *&b) const
{
return a->weight < b->weight;
}
};
int n;
int c;
int bestw;
int w[100];
int bestx[100];
void InPut()
{
printf("Number of containers and ship capacity:");
scanf("%d %d", &n, &c);
printf("%d Weight of containers:",n);
for(int i = 1; i <= n; ++i) //I of w[i] starts from 1
scanf("%d", &w[i]);
}
void AddAliveNode(priority_queue<MaxHeapQNode *, vector<MaxHeapQNode *>, cmp> &q, MaxHeapQNode *E, int wt, int i, int ch)
{
MaxHeapQNode *p = new MaxHeapQNode;
p->parent = E;
p->lchild = ch;
p->weight = wt;
p->lev = i + 1;
q.push(p);
}
void MaxLoading()
{
priority_queue<MaxHeapQNode *, vector<MaxHeapQNode *>, cmp > q; // Large top reactor
//Define remaining weight array r
int r[n + 1];
r[n] = 0;
for(int j = n - 1; j > 0; --j)
r[j] = r[j + 1] + w[j + 1];
int i = 1;
MaxHeapQNode *E;
int Ew = 0;
while(i != n + 1)
{
if(Ew + w[i] <= c)
{
AddAliveNode(q, E, Ew + w[i] + r[i], i, 1);
}
AddAliveNode(q, E, Ew + r[i], i, 0);
//Remove the next node
E = q.top();
q.pop();
i = E->lev;
Ew = E->weight - r[i - 1];
}
bestw = Ew;
for(int j = n; j > 0; --j)
{
bestx[j] = E->lchild;
E = E->parent;
}
}
void OutPut()
{
printf("The optimal loading capacity is %d\n", bestw);
printf("The items loaded are \n");
for(int i = 1; i <= n; ++i)
if(bestx[i] == 1)
printf("%d ", i); // I is the serial number of w[i]; I of w[i] starts from 1
}
int main()
{
InPut();
MaxLoading();
OutPut();
}
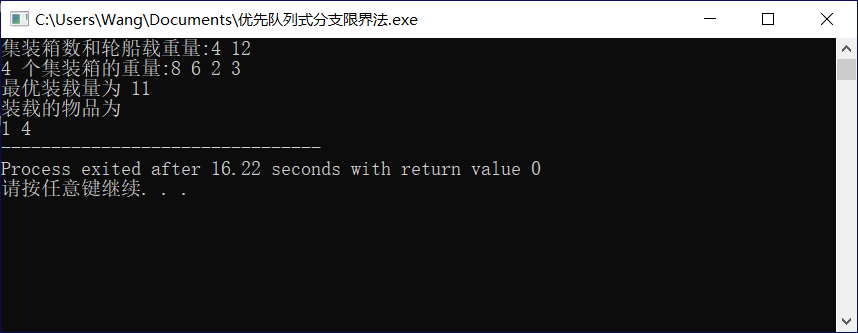
Run as shown in the figure below:
Example 2. Knapsack problem: given a group of items, each item has its own weight and price. Within the limited total weight, how can we choose to make the total price of the items the highest.
Suppose there are n items and a backpack, the weight of each item is wi, the value is vi, and each item has only one item, which can be loaded or not, which can not be separated. The backpack has a certain carrying capacity. How to load the items loaded in the backpack to maximize the value?
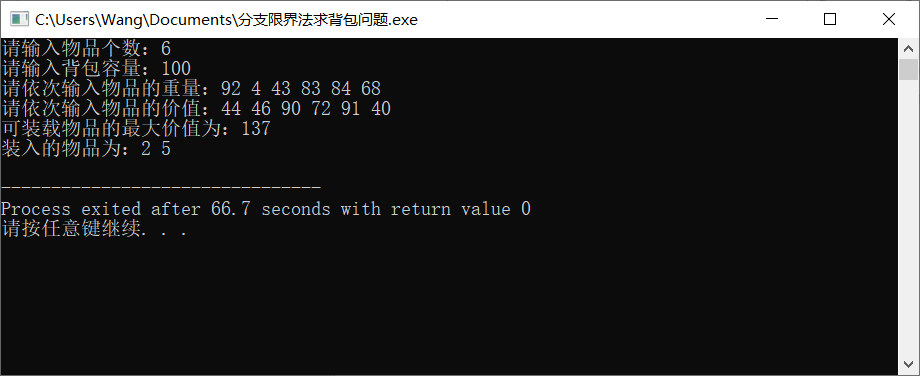
For example, there are n = 6 items, the maximum capacity of the backpack is M = 100 Kg, and the weight and value of the items are as follows:
W={92,4,43,83,84,68}
V={44,46,90,72,91,40}
Find the optimal backpack value.
The source code is as follows:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int maxn=10;
struct node
{
int cv,lv;//Current value
int lw;//Residual capacity
int id;//Item serial number
int x[maxn];//Solution vector
node()
{
memset(x,0,sizeof(x));
}
node(int cvv,int lvv,int lww,int idd)//Parameterized constructor
{
memset(x,0,sizeof(x));
cv=cvv;
lv=lvv;
lw=lww;
id=idd;
}
};//Node structure
int n,W;//Number of items, Backpack Capacity
int w[maxn],v[maxn];//Weight and value
int bestx[maxn];//Optimal solution
int bestv;//Optimal value
void init()
{
memset(w,0,sizeof(w));
memset(v,0,sizeof(v));
memset(bestx,0,sizeof(bestx));
bestv=0;
}
void bfs()
{
queue<node> q;
int sumv=0;
int i;
for(i=1; i<=n; ++i)
sumv+=v[i];
q.push(node(0,sumv,W,1));
while(!q.empty())
{
node live;
live=q.front();
q.pop();
int t=live.id;//Serial number of the item currently being processed
if(t>n||live.lw==0)//Reach the leaf node or there is no capacity
{
if(live.cv>=bestv)//Update the optimal solution. If the equal sign is not added, the first calculated value will not be updated
{
for(int i=1; i<=n; ++i)
bestx[i]=live.x[i];
bestv=live.cv;
}
continue;
}
if(live.cv+live.lv<bestv)//The gauge conditions are not met
continue;
if(live.lw>=w[t])//If the constraints are met, the left child can be generated
{
node lchild(live.cv+v[t],live.lv-v[t],live.lw-w[t],t+1);
for(int i=1; i<=n; ++i)
lchild.x[i]=live.x[i];
lchild.x[t]=1;
if(lchild.cv>bestv)//Note that the optimal value should be updated
bestv=lchild.cv;
q.push(lchild);
}
if(live.cv+live.lv-v[t]>=bestv)//The right child can be generated if the boundary conditions are met
{
node rchild(live.cv,live.lv-v[t],live.lw,t+1);
for(int i=1; i<=n; ++i)
rchild.x[i]=live.x[i];
rchild.x[t]=0;
q.push(rchild);
}
}
}
void output()
{
cout<<"The maximum value of loadable items is:"<<bestv<<endl;
cout<<"The items loaded are:";
for(int i=1; i<=n; ++i)
if(bestx[i])
cout<<i<<" ";
cout<<endl;
return ;
}
int main()
{
init();
cout<<"Please enter the number of items:";
cin>>n;
cout<<"Please enter the backpack capacity:";
cin>>W;
cout<<"Please enter the weight of the items in sequence:";
for(int i=1; i<=n; ++i) //I of w[i] starts from 1
cin>>w[i];
cout<<"Please enter the value of the item in turn:";
for(int i=1; i<=n; ++i) //I of v[i] starts from 1
cin>>v[i];
bfs();
output();
return 0;
}
Run as shown in the figure below:
https://blog.csdn.net/weixin_45591044/article/details/111089127
https://blog.csdn.net/wwj_748/article/details/9163211
https://blog.csdn.net/Luoxiaobaia/article/details/109725604
https://www.freesion.com/article/9394920015/
https://cloud.tencent.com/developer/article/1616376
https://blog.csdn.net/vxiao_shen_longv/article/details/98481660