1, Depth first search (BFS)
1. Introduction
BFS, its full English name is bread first search. BFS does not use rule of thumb algorithms. From the point of view of the algorithm, all child nodes obtained by expanding nodes will be added to a first in first out queue. In general experiments, the nodes whose neighbor nodes have not been verified will be placed in a container called open (such as queue or linked list), while the verified nodes will be placed in a container called closed. (open closed table)
breadth first search is an algorithm for searching graphs. Suppose we start at a vertex (i.e. the starting point), we don't know the overall structure of the graph, and our purpose is to search along the edge from the starting point until we reach the specified vertex (i.e. the end point). In this process, every time we reach a vertex, we will judge whether it is the end point. Breadth first search starts first from the vertex near the starting point.
in the process of performing breadth first search, a breadth first tree will be constructed. At first, the tree contains only the root node, which is the source node s. When scanning the adjacent linked list of discovered node u, whenever a white node V is found, node V and edge (U, v) are added to the tree at the same time. In the breadth first tree, node u is called the precursor or parent of node v. Since each node can be found at most once, it has at most one parent node. The ancestor and descendant relationship in the breadth first tree is defined by the position relative to the root node s: if node u is a node on the simple path from root node s to node V, node u is the ancestor of node V and node V is the descendant of node U.
2. Steps
breadth first search is similar to the hierarchical traversal of a tree.
suppose that starting from a vertex v in the graph, after accessing V, each unreachable adjacency point of V is accessed in turn, and then their adjacency points are accessed in turn from these adjacency points, so that the "adjacency point of the first accessed vertex" is accessed before the "adjacency point of the later accessed vertex", Until the adjacency points of all accessed vertices in the graph are accessed. If there are still vertices in the graph that have not been accessed, select another vertex in the graph that has not been accessed as the starting point, and repeat the above process until all vertices in the graph are accessed. In other words, the breadth first search process takes V as the starting point, from near to far, and successively accesses the vertices connected with V with path lengths of 1, 2.
data structure queue used by the adjacency point to be accessed.
- Add the initial point (one or more) to the tail of a set
- Take out the points from the collection head, judge the surrounding points of the initial point, and add the qualified points to the queue
- Repeat 2 until the collection is empty. (generally, each point is added to the queue only once)
Applicable:
- In general, BFS is more likely to be used in trees or graphs. (shortest path)
3. Illustration
the green node is the point to be searched, the dark gray is the point not accessed, and the light gray is the point already accessed.
add the starting point to the queue first. Take the queue header to search (node s).
you need to set a flag whether a node has accessed.
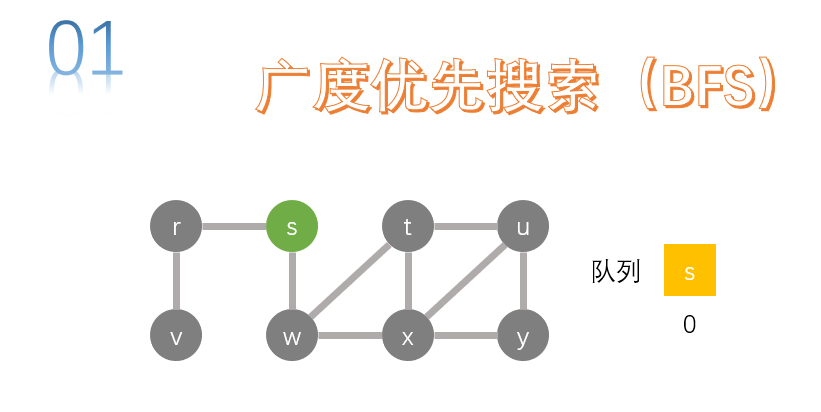
search the adjacency point of s, r and W are the adjacency points of s, and add r and w to the queue.
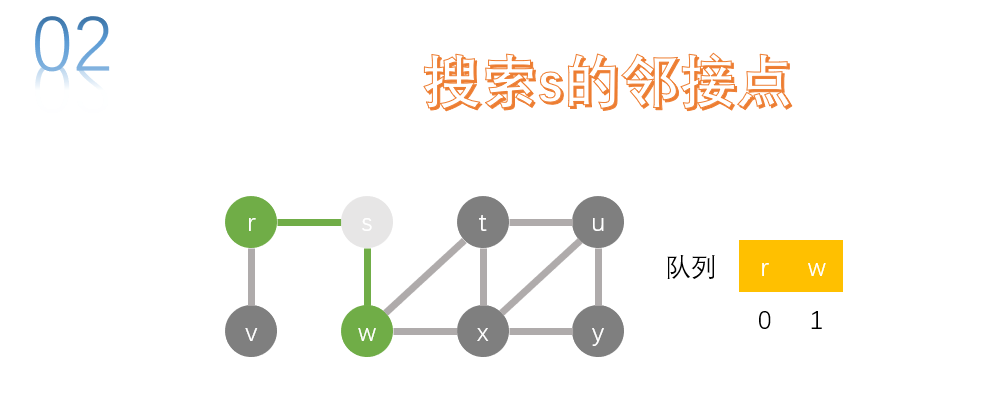
take the first node r of the queue and search. v is the adjacency point of R. add v to the queue.
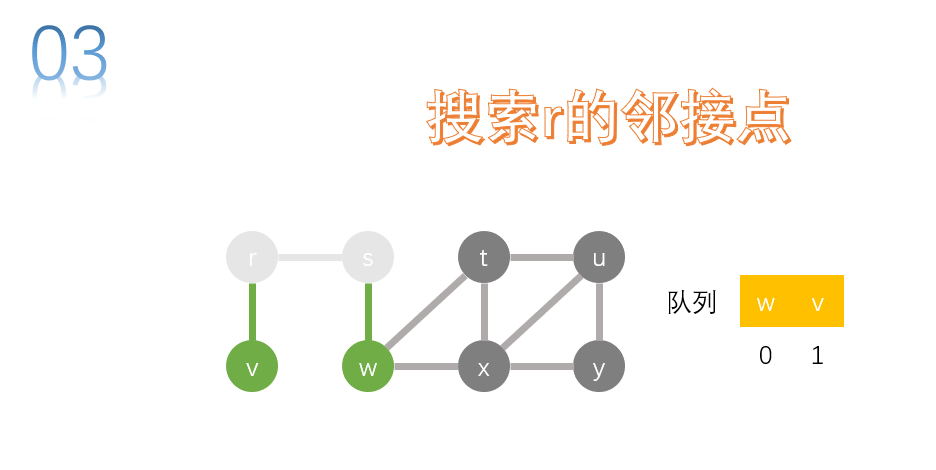
take the first node w of the team and search. t. x is the adjacency point of W, and T and x are added to the queue.
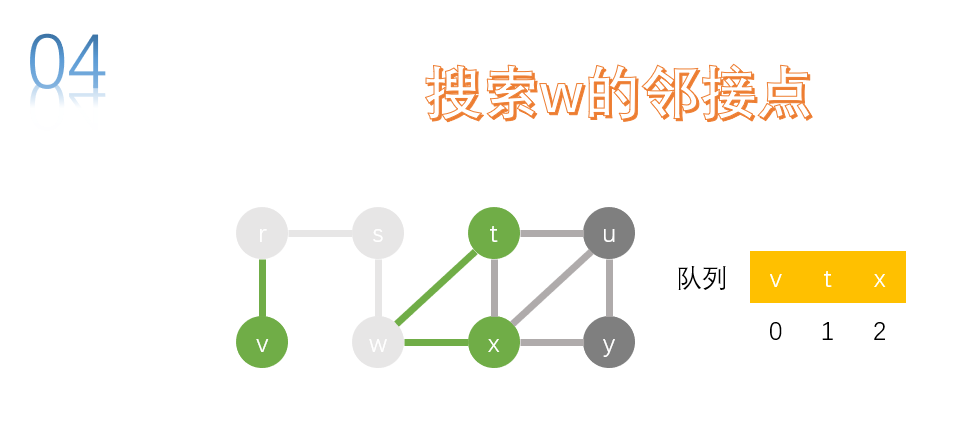
take the first node v of the team and search. v no adjacent contact.
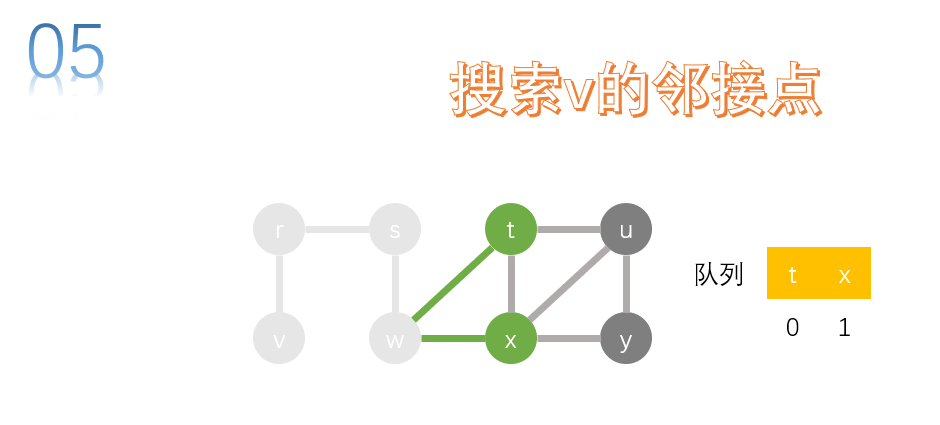
take the first node t of the team and search. u. x is the adjacency of t, and x has accessed it, so u is added to the queue.
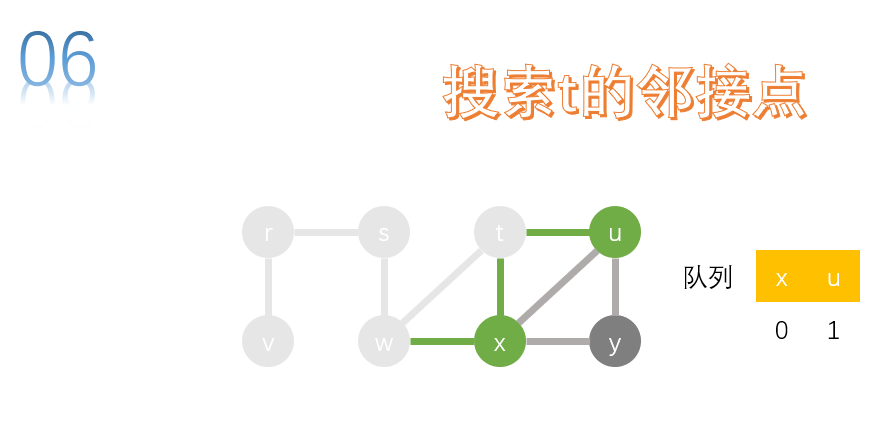
take the first node x of the team and search. w. T, u and y are the adjacency points of x. W, t and u have been accessed, so y is added to the queue.
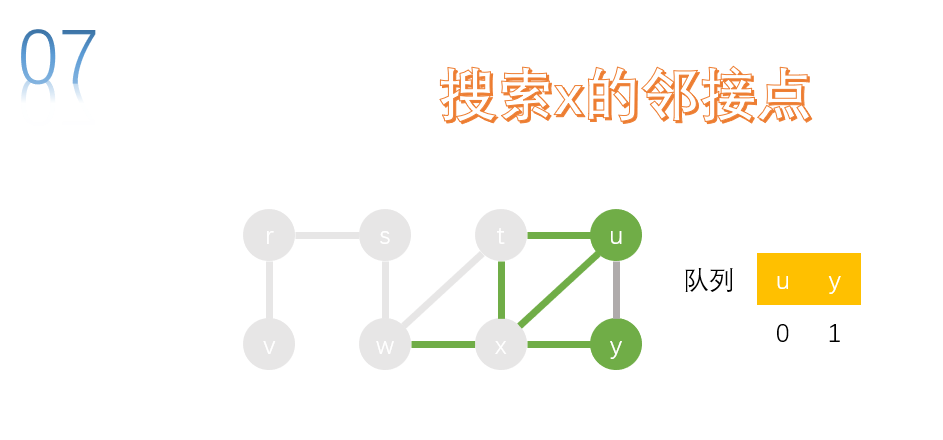
take the first node U of the team and search. t. x and y are the adjacency points of u, t, x and y have been accessed, and no node needs to join the queue.
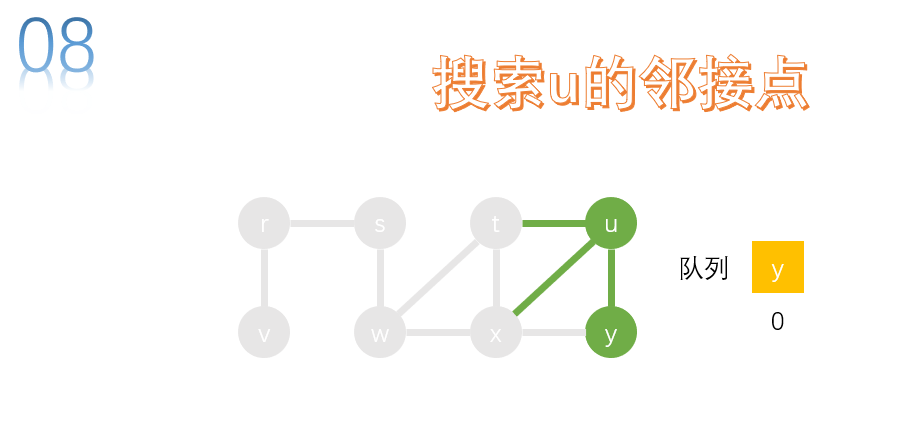
take the first node y of the team and search. u. x is the adjacency point of Y. u and x have been accessed and do not need to join the queue.
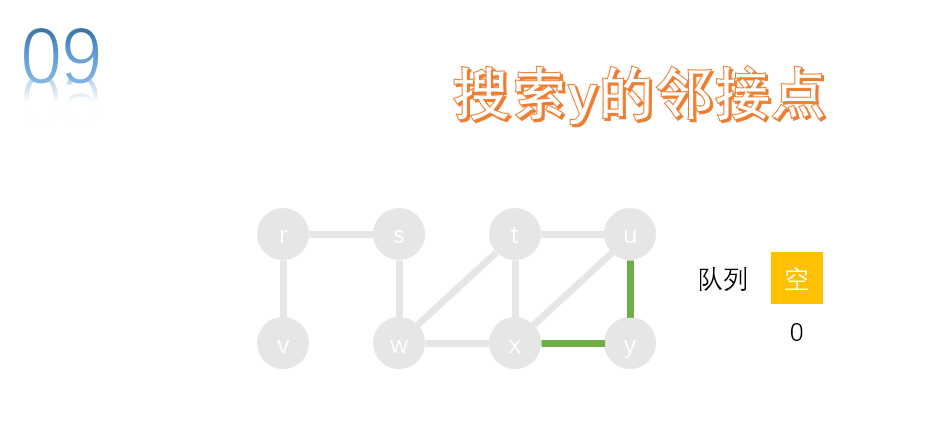
the queue is empty. End the breadth first search (BFS).
access order: s, r, w, v, t, x, u, y
each node enters the queue at most once. Breadth first search is characterized by extensive search from near to far from the starting point. Therefore, the closer the target vertex is to the starting point, the faster the search ends.
Examples
First question
Title Link
Template question
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> printFromTopToBottom(TreeNode* root) {
vector<int> num;
if(!root)
return num;
queue<TreeNode*> p;
p.push(root);
while(!p.empty()){
TreeNode* s = p.front();
p.pop();
num.push_back(s->val);
if(s->left)
p.push(s->left);
if(s->right)
p.push(s->right);
}
return num;
}
};
Second question
Title Link
Add all points with 1 to the queue for bfs.
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int n,m;
int A[1010][1010],B[1010][1010];//Such as the meaning of the title
queue<pair<int,int> >q;//queue
int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};//Coordinate transformation of up, down, left and right directions
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ ){
int a;
scanf("%1d", &a);
B[i][j] = -1;
if(a == 1){//Add all points of 1 to the queue and set B to 0
B[i][j] = 0;
q.push({i,j});
}
}
int cnt = 0;//What level is the record
while(q.size()){//Queue is not empty
int f = q.size();//Get the number of this layer
cnt++;
for (int i = 0; i < f; i ++ ){//Click the of this layer out of the queue in turn
pair<int, int> next = q.front();//Get the value of team leader
q.pop();//First out of queue
int x = next.first, y = next.second;
for (int j = 0; j < 4; j ++ ){//Traverse four directions
if (x+dx[j]>=0 && x+dx[j]<n && y+dy[j]>=0 && y+dy[j]<m && B[x+dx[j]][y+dy[j]]==-1){//The coordinates are in the map, and this point has not been expanded
B[x+dx[j]][y+dy[j]] = cnt;
q.push({x+dx[j], y+dy[j]});//Add the satisfied conditions to the queue
}
}
}
}
for (int i = 0; i < n; i ++ ){
for (int j = 0; j < m; j ++ )
printf("%d ",B[i][j]);
printf("\n");
}
return 0;
}
Question 3
#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
using namespace std;
int n,m;
char str[510][510];
int d[510][510];//Record the minimum value from the starting point to this point
int bfs(){
memset(d,0x3f,sizeof(d));
deque<pair<int, int>> dp;
dp.push_back({0,0});//Add the starting point to the end of the queue
d[0][0] = 0;
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};//Displacement in four directions
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};//Get the line of the grid (each grid is marked with the upper left corner)
char s[] = "\\/\\/";//Four different directions, diagonal
while(dp.size()){
pair<int, int> f = dp.front();//Go to queue head
dp.pop_front();//Remove queue header
int x = f.first, y = f.second;
for (int i = 0; i < 4; i ++ ){//Traverse four directions
int xx = x + dx[i], yy = y + dy[i];
if(xx >= 0 && xx<=n && yy>=0 && yy<=m){//Verify that the direction is legal
int w = 0;
if(s[i] != str[x+ix[i]][y+iy[i]])//There is no path in the direction, and the path direction needs to be changed
w = 1;
if(d[xx][yy] > d[x][y]+w){//If the value reaching this point is greater than the value of the current scheme, replace the minimum value
d[xx][yy] = d[x][y]+w;
if(w)//If you need to change the direction, add it to the end of the queue
dp.push_back({xx,yy});
else//If you do not need to change the direction, add it to the head of the queue
dp.push_front({xx,yy});
}
}
}
}
if(d[n][m] == 0x3f3f3f3f)//Verify that it is the initial value
return 0;
return 1;
}
int main()
{
int t;
scanf("%d",&t);
while (t -- ){
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ){
scanf("%s", str[i]);
}
if(bfs())
printf("%d\n",d[n][m]);
else
printf("NO SOLUTION\n");
}
return 0;
}
Question 4
Title Link
Template question
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
pair<int, int> start,endd;
int n,m;
char str[160][160];
int d[160][160];
int bfs(){
queue<pair<int, int>> q;
q.push(start);
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
while(q.size()){
auto a = q.front();
q.pop();
for (int i = 0; i < 8; i ++ ){
int x = a.first + dx[i], y = a.second + dy[i];
if(x<0 || x>=n || y<0 || y>=m || str[x][y] == '*' || d[x][y] != 0)
continue;
d[x][y] = d[a.first][a.second] + 1;
if(x == endd.first && y == endd.second)
return d[x][y];
q.push({x,y});
}
}
return -1;
}
int main()
{
scanf("%d%d", &m, &n);
for (int i = 0; i < n; i ++ ){
getchar();
for (int j = 0; j < m; j ++ ){
scanf("%c", &str[i][j]);
if(str[i][j] == 'K')
start = {i,j};
else if(str[i][j] == 'H')
endd = {i,j};
}
}
printf("%d",bfs());
return 0;
}
2, Breadth first search (DFS)
1. Introduction
an algorithm used to traverse or search a tree or graph. Traverse the nodes of the tree along the depth of the tree and search the branches of the tree as deep as possible. When the edges of node v have been explored or the node does not meet the conditions during the search, the search will be traced back to the starting node of the edge where node v is found. The whole process repeats until all nodes are accessed. In the worst case, the time complexity of the algorithm is O(!n).
2. Steps
assuming that the initial state is that all vertices in the graph have not been accessed, the depth first search can start from a vertex v in the graph, access this vertex, and then start from the unreachable adjacency of V in turn to search the graph until all vertices connected with V by the path in the graph are accessed; If there are still vertices in the graph that have not been accessed, select another vertex in the graph that has not been accessed as the starting point, and repeat the above process until all vertices in the graph are accessed.
starting from a vertex v in the figure:
- Access vertex v;
- Starting from the unreachable adjacency points of v, the depth first traversal of the graph is carried out; Until the vertices connected with v paths in the graph are accessed;
- If there are still vertices in the graph that have not been accessed at this time, start from a vertex that has not been accessed and repeat the depth first traversal until all vertices in the graph have been accessed.
3. Illustration
green is the current node, dark gray is the unreachable node, and light gray is the accessed node.
set the starting point as node s for depth first search. Generally, the path of DFS is recorded using stack or recursion.
you need to set a flag whether a node has accessed.
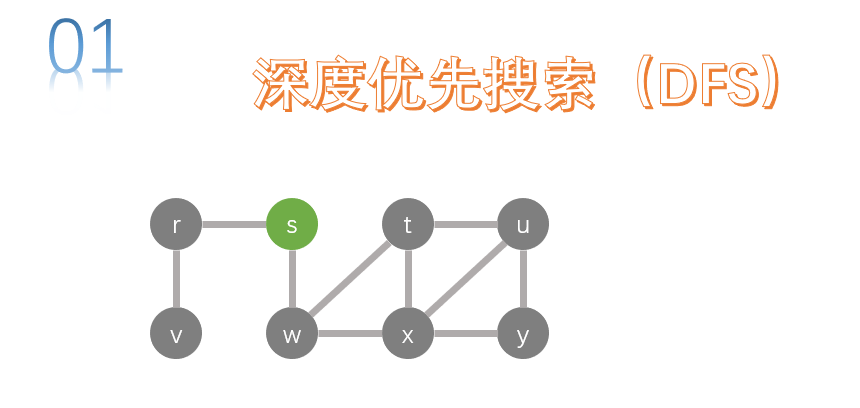
R and w are the adjacency points of S. let's search node r first. Perform a depth first search on R.
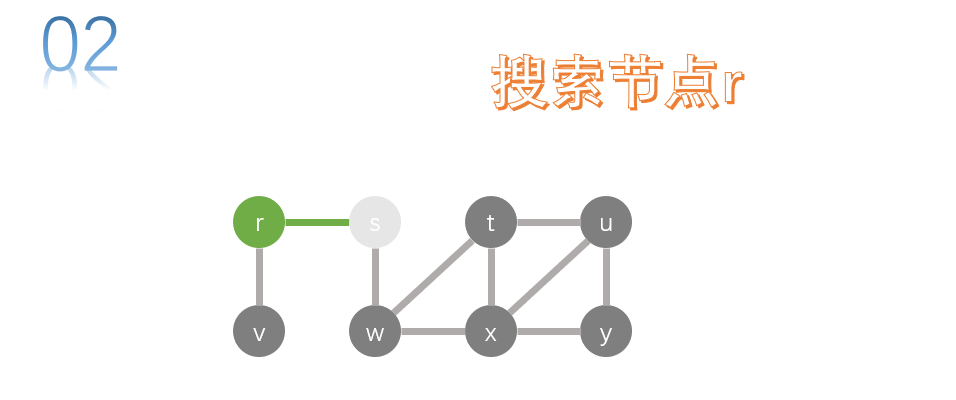
The adjacency point of r as long as node V, all we search for V. Perform a depth first search on v.
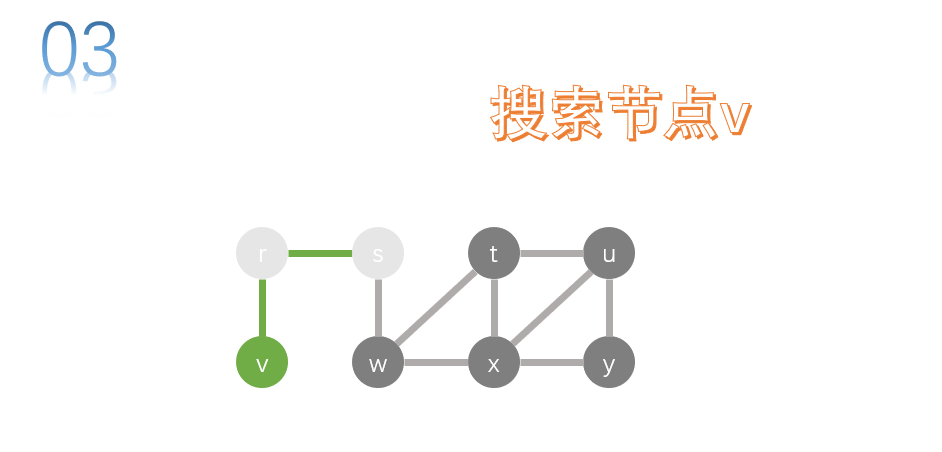
v has no adjacency point, which means that in the end, it should return to the previous node, that is, return r and search for other adjacency points of r.
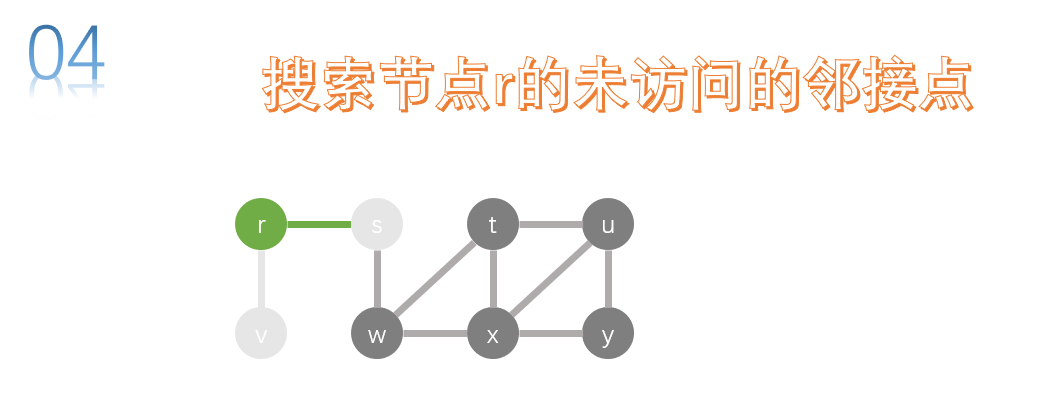
as long as v has an adjacent contact, it has been accessed, and all r have no unreachable adjacent points, so it should return the upper level of R, that is, return s, and search for the unreachable adjacent points of S.
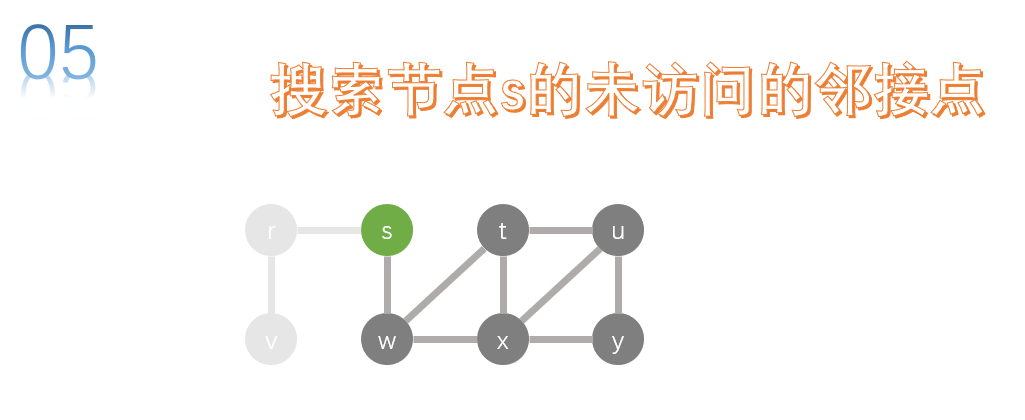
The adjacency points of s have r and W, and W is not accessed, so we search w next. Perform a depth first search on W.
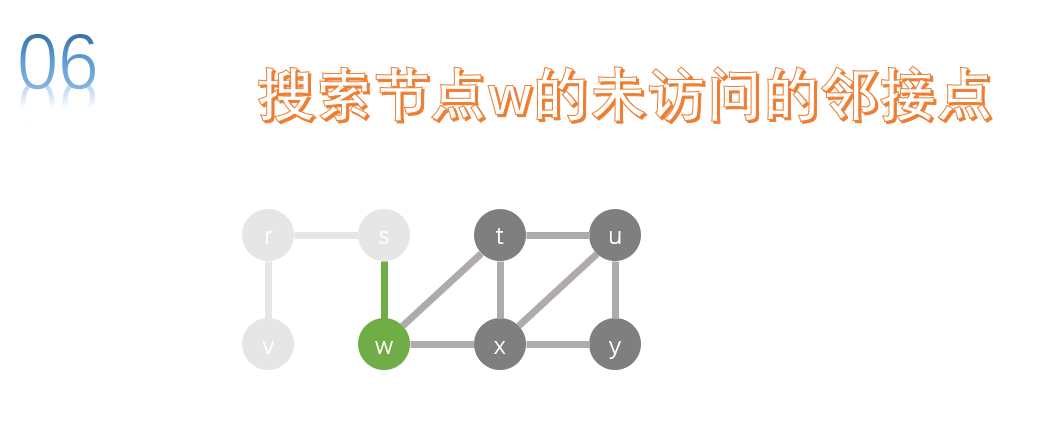
The adjacency points of w have t and x. neither node is accessed. Let's access t first. Perform a depth first search on t.
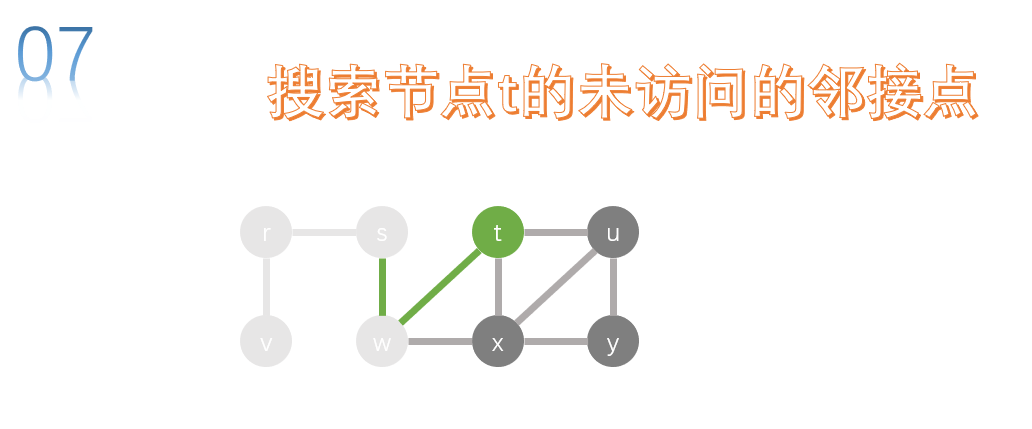
The adjacency points of t are u, x and W. w has been accessed, so there are only u and x. let's search u first.
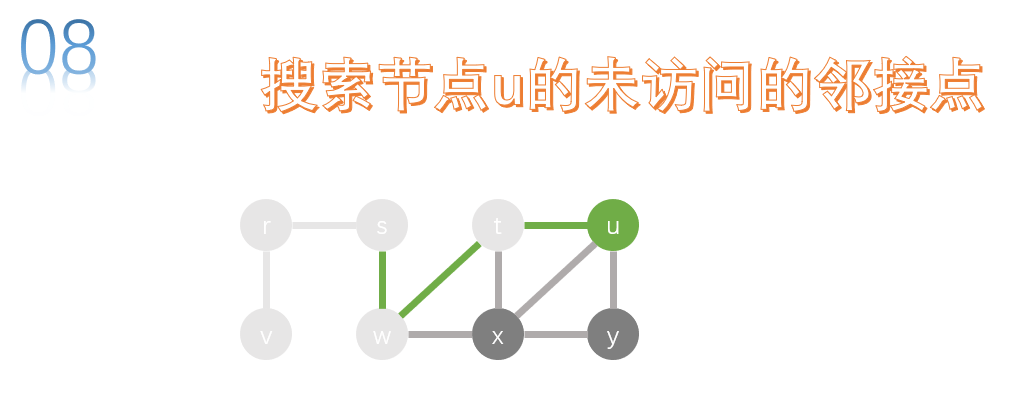
The adjacency points of u are y, X and t. t has been accessed, so there are only x and Y. let's search y first.
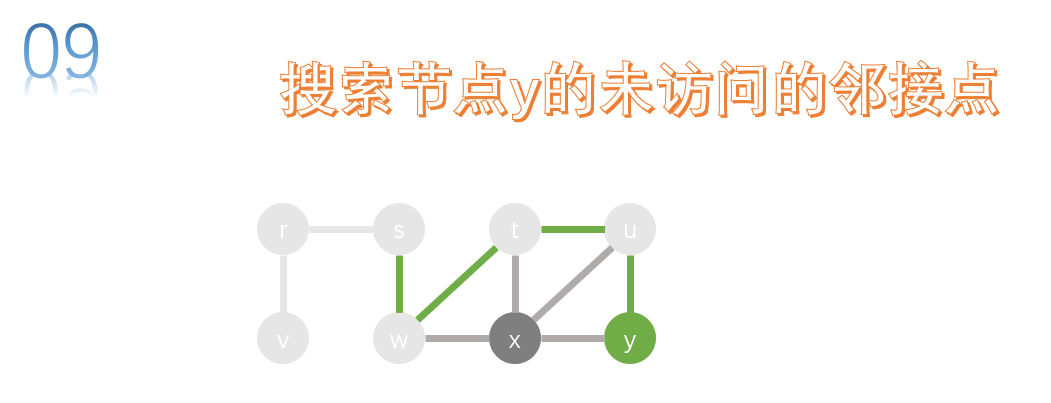
The adjacency points of y have x and u, and u has been accessed, so we search x.
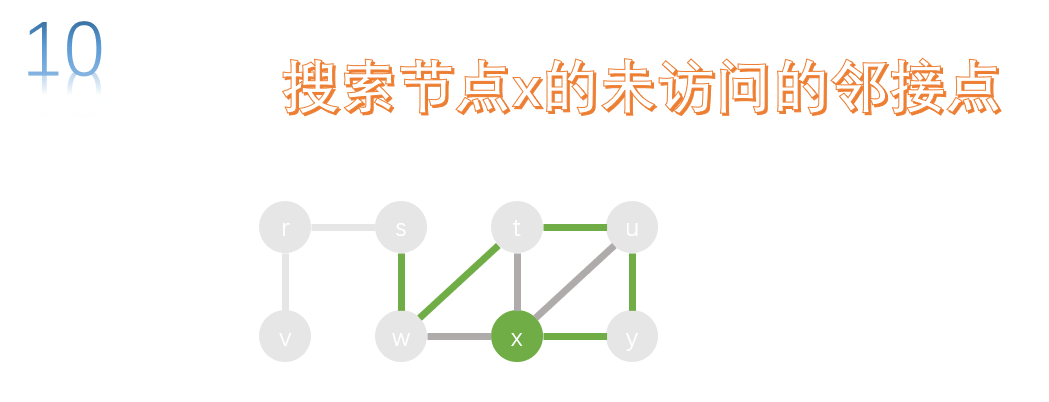
The adjacency points of x include w, t, u and y, which have been accessed, so x can't continue. We nine return to the previous node, that is, return y, and search the unreached adjacency points of Y.
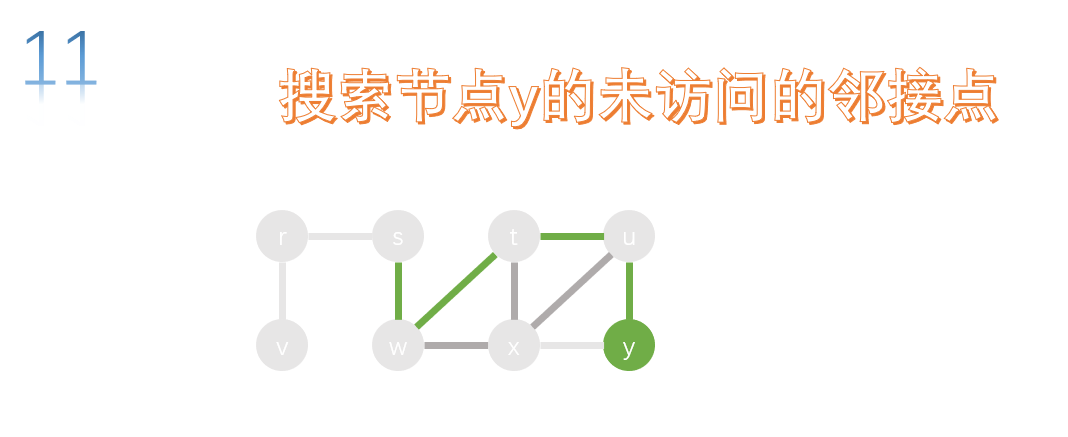
All adjacency points of y have been accessed, so return to the previous node u and search the unreached adjacency points of U.
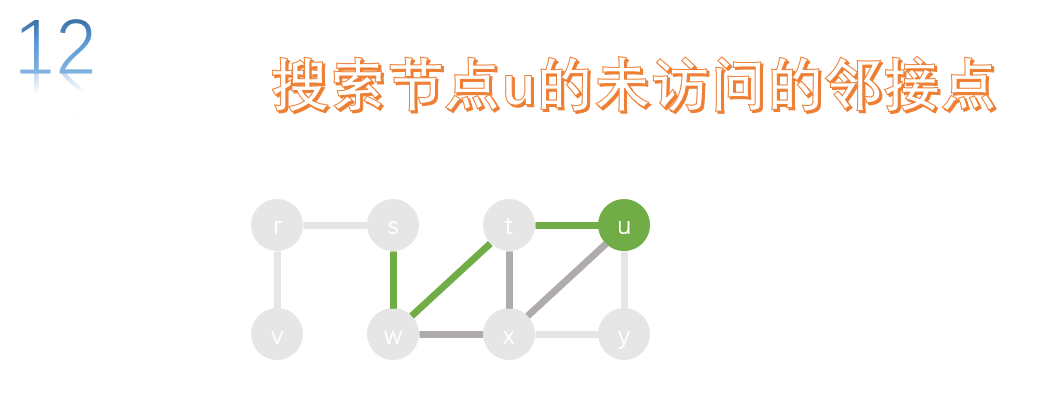
All adjacency points of u have been accessed, so return to the previous node t and search the unreached adjacency points of t.
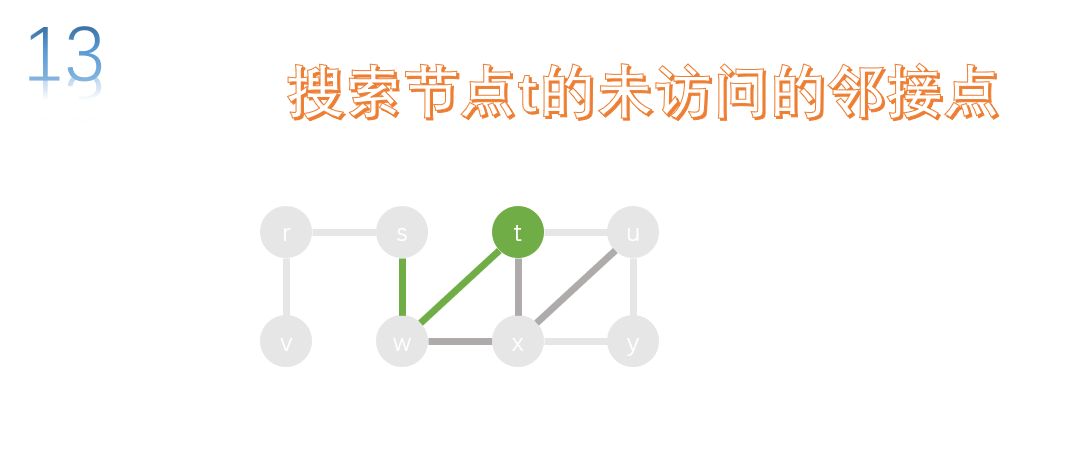
All adjacency points of t have been accessed, so return to the previous node w and search the unreached adjacency points of w.
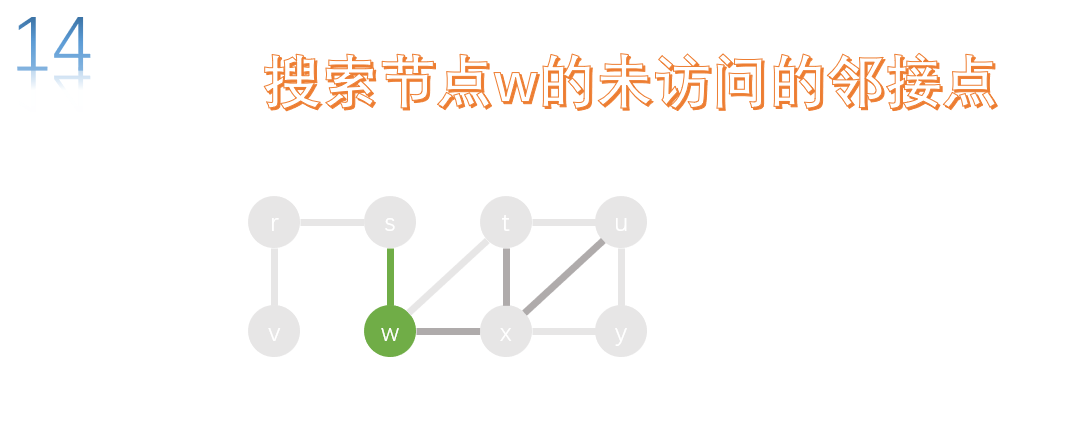
All adjacency points of w have been accessed, so return to the previous node s and search the unreached adjacency points of S.
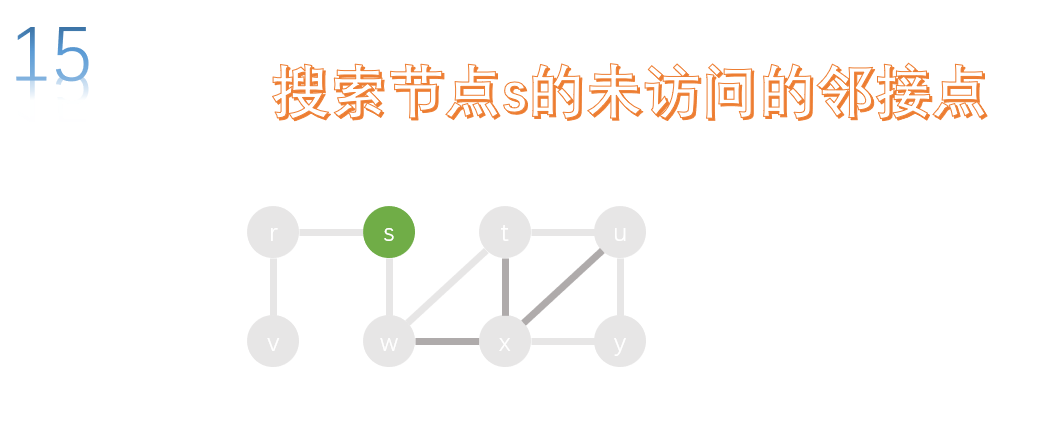
All adjacency points of w have been accessed, and s has no upper level node, so the depth first search is over.
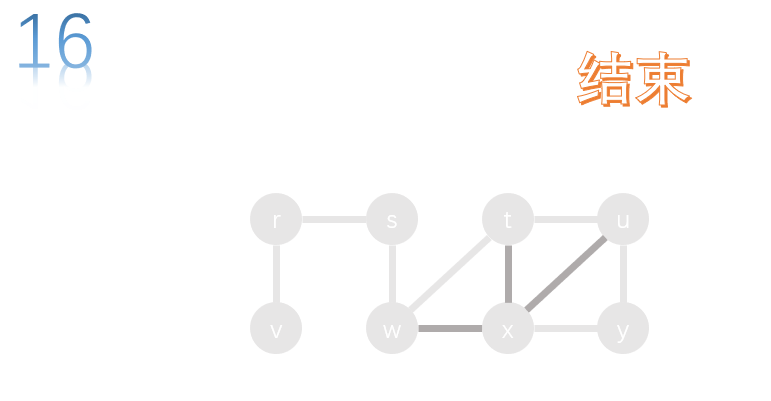
access order: s, r, v, w, t, u, y, x
the order of access and breadth first search will be different, but their time complexity is the same.
Examples
First question
Simple template question
#include<stdio.h>
int n,m;//quantity
int num[100];//Data sequence of record arrangement
void recurrence(int f,int l){//DFS recursion
int i,j;
if(f == m+1){//A sequence meets the requirements
for(i=1;i<=m;i++)//Output sequence
printf("%d ",num[i]);
printf("\n");
return;//Returns the previous number
}
for(i=l;i<=n;i++){//Loop through all unused numbers
num[f] = i;//Mark that the number is already in use
recurrence(f+1,i+1);//Traverse the next number
num[f] = 0;//Mark that the number is not used
}
}
int main()
{
scanf("%d %d",&n,&m);
recurrence(1,1);
return 0;
}
Second question
Add a condition to whether to enter the next grid.
class Solution {
public:
int n,m,k;
int cnt = 0;//Record how many squares there are
int flag[51][51];//Record whether x and j positions have passed
int computer(int a){//Calculate the sum of the numbers on each bit of number a
int count = 0;
while (a){
count += a%10;
a /= 10;
}
return count;
}
void dfs(int x,int y){//Deep search
if(computer(x)+computer(y)>k || x<0 || y<0 || x>=n || y>=m || flag[x][y]==1)//Unqualified points skip
return;
cnt++;//Record that the point meets the requirements
flag[x][y] = 1;//The marking point has passed
//Whether the four points up, down, left and right are consistent
dfs(x+1,y);
dfs(x,y+1);
dfs(x-1,y);
dfs(x,y-1);
}
void bfs(){
queue<pair<int,int>> q;//Sequence of queue record points
q.push({0,0});//Queue starting point
while(!q.empty()){//Cycle until the point is empty
auto a = q.front();//Get queue header
q.pop();//First out of queue
int x = a.first, y = a.second;
if(computer(x)+computer(y)>k || x<0 || y<0 || x>=n || y>=m || flag[x][y]==1)//Unqualified points skip
continue;
cnt++;//Record that the point meets the requirements
flag[x][y] = 1;//The marking point has passed
//Whether the four points up, down, left and right are consistent
q.push({x+1,y});
q.push({x,y+1});
q.push({x-1,y});
q.push({x,y-1});
}
}
int movingCount(int threshold, int rows, int cols)
{
k = threshold;
n = rows;
m = cols;
// dfs(0,0);
bfs();
return cnt;
}
};
Question 3
Use dfs to simulate inbound and outbound, traverse all possible and print.
#include<stdio.h>
int n;//quantity
int num[100],stop[100],f=0,m=0;//Record the data sequence of the railway station stack
int flag[100];
int cnt = 0;
void dfs(int x){//DFS recursion simulates the stack entry and stack exit
if(f>0){//Out of stack
num[m++] = stop[--f];
dfs(x);
stop[f++] = num[--m];
}
if(x <= n){//Enter the stack
stop[f++] = x;
dfs(x+1);
f--;
}
if(x == n+1 && cnt < 20 && f == 0){//Meet the requirements and print the results
cnt++;
for(int i=0;i<n;i++)
printf("%d",num[i]);
printf("\n");
}
}
int main()
{
scanf("%d",&n);
dfs(1);
return 0;
}
Question 4
Data is small, direct use of dfs violence to simulate all cases, to the smallest. However, using dfs directly will time out. We need to optimize dfs:
- When the number of cable cars is greater than or equal to the known minimum value, the scheme can be ended directly.
- Ranking the weight of cats, we perform dfs from large to small, which can reduce the combination of cars.
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n,w;
int num[20], car[20];
int cnt = 20;
void dfs(int f,int k){
if(k >= cnt)//The number of cable cars has been greater than or equal to the known minimum number of cable cars
return;
if(f < 0){//The cats have all got on the bus
if(cnt > k)//The number of cable cars in the current scheme is the smallest
cnt = k;
return;
}
for(int i=0;i<k;i++)//Traverse all cable cars
if(car[i]+num[f] <= w){//Judge whether you can share one seat
car[i] += num[f];
dfs(f-1, k);
car[i] -= num[f];
}
car[k++] = num[f];//Drive another cable car
dfs(f-1, k);
k--;
}
int main()
{
scanf("%d %d",&n,&w);
for(int i=0;i<n;i++)
scanf("%d",&num[i]);
sort(num,num+n);//Sort, from small to large
dfs(n-1, 0);//dfs
printf("%d",cnt);
return 0;
}
3, Summary
depth first search is characterized by continuous downward search along a path. Although breadth first search and depth first search have great differences in search order, there is only one difference in operation steps, that is, which candidate vertex is selected as the benchmark of the next vertex is different.
breadth first search selects the vertex that becomes the candidate first. Because the vertex becomes the candidate earlier the closer it is to the starting point, it will start searching in order from the place close to the starting point; The depth first search selects the vertices that have recently become candidates, so it will continue to search deeply along the newly discovered path.