Merge two ordered arrays

Title address: Merge two ordered arrays

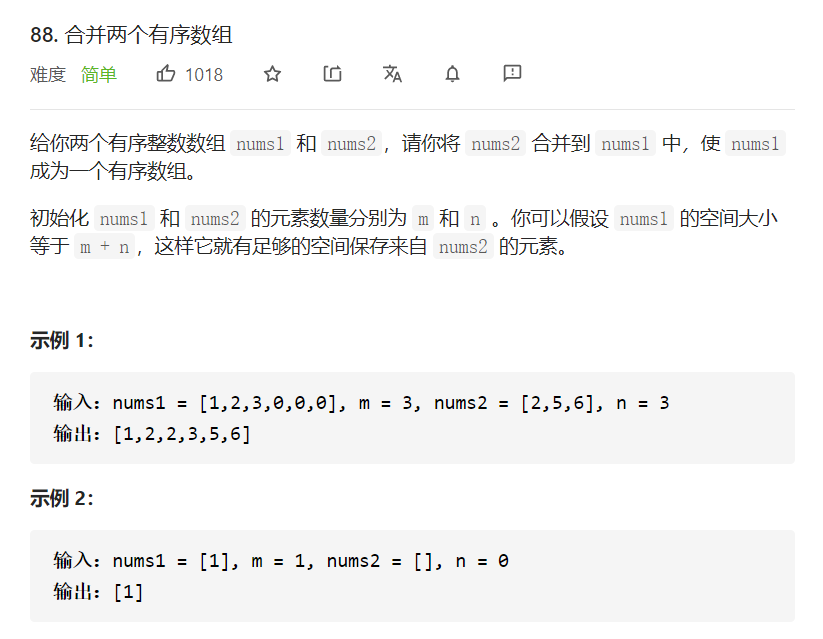
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        // Double pointer solution
        // Define two pointers
        int p1=0,p2=0;
        // Define temporary variable assignment
        int temp;
        // Define sort array
        int[] sort=new int[m+n];
        while(p1<m|p2<n){
            // m0 directly assigns temp
            if(p1==m){
                temp=nums2[p2++];
            }
            else if(p2==n){
                temp=nums1[p1++];
            }else if(nums1[p1]<nums2[p2]){
                // p1 here, assign values first and then++
                temp=nums1[p1++];
            }else{
                temp=nums2[p2++];
            }
            // Controls the assignment of sorted arrays
            sort[p1+p2-1]=temp;
        }
        for(int i=0;i!=m+n;i++){
            nums1[i]=sort[i];
        }
    }
}

Complexity analysis

• Time complexity: O(m+n)O(m+n).
  The pointer moves monotonically, moving m+n times at most, so the time complexity is O(m+n)O(m+n).

• Spatial complexity: O(m+n)O(m+n).
  You need to create an intermediate array sorted with a length of m+n.

Solution 2

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        for (int i = 0; i != n; ++i) {
            nums1[m + i] = nums2[i];
        }
        Arrays.sort(nums1);
    }
}

Valid Letter ectopic words

Title address: Valid Letter ectopic words

Solution 1

class Solution {
    public boolean isAnagram(String s, String t) {
        if(s.length()!=t.length()){
          return false;
        }
         char[] str1 = s.toCharArray();
        char[] str2 = t.toCharArray();
        Arrays.sort(str1);
        Arrays.sort(str2);
        return Arrays.equals(str1, str2);
    }
}

Solution 2

See the big guy's ideas, immediately worship, and record this solution here!

Original link: The array as a hash table to use, very clever!

Array is actually a simple hash table. In this topic, the string has only lowercase letters. You can define an array to record the number of characters in string s and how large the array is, because there are 26 English letters

Move up! Judge the next string s="aee",t="eae"

Define an array record to record the number of characters in the string s

The characters need to be mapped to the array, that is, the hash table index. Because the ASCll from character a to character Z is 26 consecutive values, the following table of character a is 0. When the corresponding character Z is mapped to the following table 25 and traversing the string s, you only need to operate the element + 1 where s [i] - [a 'is located. You don't need to remember the ASCll of character a, just find a relative value, In this way, the number of characters in the string s is counted.
Let's see how to check whether these characters appear in string T. similarly, when traversing string t, do - 1 operation on the value on the hash table index of the character mapping hash table that appears in t.
Finally, check that if some elements of the record array are not zero, it means that the strings s and t must be who has more or less characters. return false.
Finally, if all elements of the record array are zero, it means that the strings s and t are alphabetic ectopic words, return true.

The time complexity is O(n), and the space complexity is O(1) because it is defined as a constant size auxiliary array

class Solution {
    public boolean isAnagram(String s, String t) {
         int[] record=new int[26];
        for (char c : s.toCharArray()) {
            record[c-'a']+=1;
        }
        for (char c : t.toCharArray()) {
            record[c-'a']-=1;
        }
        for (int i : record) {
            if (i!=0){
                return false;
            }
        }
        return true;
    }
}

The language description is very abstract. You can put it into the IDE and DEBUG it yourself

Intersection of two arrays

Title address: Intersection of two arrays

Idea:

Use two sets to remove duplicate elements by using features, add the elements in Set1 to Set2, and finally convert them into an array and return!

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        //Create a Set collection to remove duplicate elements
         Set<Integer> set1 = new HashSet<Integer>();
        Set<Integer> set2 = new HashSet<Integer>();
        for (int num : nums1) {
            set1.add(num);
        }
        for (int num : nums2) {
            set2.add(num);
        }
        return getIntersection(set1, set2);
    }

    public static int[] getIntersection(Set<Integer> set1, Set<Integer> set2) {
        if (set1.size() > set2.size()) {
            return getIntersection(set2, set1);
        }
        // Add the element of set1 to set2
        HashSet<Integer> integerHashSet = new HashSet<Integer>();
        for (Integer item : set1) {
            if (set2.contains(item)) {
                integerHashSet.add(item);
            }
        }
        // Convert to array and return
        int[] intersection = new int[integerHashSet.size()];
        int index = 0;
        for (int num : integerHashSet) {
            intersection[index++] = num;
        }
        return intersection;
    }
}

Complexity analysis

• Time complexity: O(m+n)O(m+n), where mm and nn are the lengths of the two arrays respectively. Using two sets to store the elements in two arrays requires O(m+n)O(m+n) time, traversing the smaller set and judging whether the elements need O(min(m,n))O(min(m,n)) time in another set. Therefore, the total time complexity is O(m+n)O(m+n).

• Space complexity: O(m+n)O(m+n), where mm and nn are the lengths of the two arrays respectively. The spatial complexity mainly depends on two sets.

Sum of two numbers

Title address: Sum of two numbers

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] + nums[j] == target) {
                    int[] res=new int[]{i, j};
                    return res;
                }
            }
        }
        return new int[0];
    }
}

Complexity analysis

• Time complexity: O (N2) O (N2), where n is the number of elements in the array. In the worst case, any two numbers in the array will be matched once.

• Spatial complexity: O(1)O(1).

The code is submitted and passed by the force deduction compiler. Please point out the improper writing in the comment area 💪!