preface
- There are too few problems in dynamic programming. Brush some problems, practice the awareness of solving problems with dynamic programming and know some common skills.
- Each question in the article has written some important points and ideas for me to understand this question.
- If you have any questions, please comment.
1. Sword finger Offer 10- I. Fibonacci sequence [easy]
Go and do the problem
Write a function, enter n, and find the nth term of the Fibonacci sequence (i.e. F(N)). Fibonacci sequence is defined as follows:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), where n > 1
The Fibonacci sequence starts with 0 and 1, and the subsequent Fibonacci numbers are obtained by adding the previous two numbers.
The answer needs to take the module 1e9+7 (100000007). If the initial result is 100000008, please return 1.
Input: n = 2
Output: 1
Fibonacci sequence is a very simple and familiar problem
- dp[0] = 0
dp[1] = 1 - dp[n] = dp[n-1] + dp[n-2]
- Because F(N) is only related to F(N-1) and F(N-2), the space complexity can be optimized to O(1) by using [rolling array idea] without using arrays.
public int fib(int n) {
int[] dp = new int[n+1];
if(n < 2)return n;
else{
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i<=n; i++)
dp[i] = (dp[i-1] + dp[i-2])%1000000007;
}
return dp[n];
}
//Space optimization is O(1)
public int fib(int n) {
if(n < 2) return n;
int f0 = 0, f1 = 1, fn = 0;
for(int i=2; i<=n; i++){
fn = (f0 + f1)%1000000007;
f0 = f1;
f1 = fn;
}
return fn;
}
2. Sword finger Offer 10- II. Frog jumping steps [easy]
Go and do the problem
A frog can jump up one step or two steps at a time. Find out how many jumping methods the frog can jump up an n-step.
The answer needs to take the module 1e9+7 (100000007). If the initial result is 100000008, please return 1.
Input: n = 7
Output: 21
Similar to the Fibonacci sequence.
- dp[n] indicates how many jumping methods there are to jump up n steps
- dp[0] = 1
dp[1] = 1 - dp[n] = jump method of jumping up (n-1) steps + jump method of jumping up (n-2) steps
- It is the same as Fibonacci sequence, eliminating the need to open up array space.
public int numWays(int n) {
if(n < 2) return 1;
int f0 = 1, f1 = 1, fn = 0;
for(int i = 2; i<=n; i++){
fn = (f0 + f1)%1000000007;
f0 = f1;
f1 = fn;
}
return fn;
}
3. Sword finger Offer 19. Regular expression matching [hard]
Go and do the problem
Please implement a function to match regular expressions containing '.' and '*'. The character '.' in the mode indicates any character, while '*' indicates that the character before it can appear any time (including 0 times)
In this question, matching means that all characters of the string match the whole pattern.
For example, the string "aaa" matches the patterns "a.a" and "ab*ac*a", but does not match "aa.a" and "ab*a".
Input:
s = "aa"
p = "a"
Output: false
- p is the regular expression containing '.' and '*', and s is the string
- Boolean type dynamic programming matrix. dp[i][j] represents whether the first I characters of string s and the first j characters of p can match.
- dp[0][0] = true
Initialize the first line, that is, when s is an empty string, DP [0] [J] = DP [0] [J - 2] & & P [J - 1] = '*'
For example, if p = 'a*b *', you can match the empty string, that is, make both a and B appear 0 times - Since dp[0][0] represents the state of empty characters, the added characters corresponding to dp[i][j] are s[i - 1] and p[j - 1]
Consider the newly added characters p[j-1] = = '*' and p[j-1]! = '*'
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length() + 1, n = p.length() + 1;
boolean[][] dp = new boolean[m][n];
dp[0][0] = true;
// Initialize first line
for(int j = 2; j < n; j += 2)
// dp[0][j] = true if dp[0][j-2] = true and p[j-1] = '*'
// For "a*b *", it means p[1]='*',p[3] = '*'
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
// state transition
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if(p.charAt(j - 1) == '*') {
// 1. Do the first s[i] and p[j-2] match, [] * match 0 times
if(dp[i][j - 2])
dp[i][j] = true;
// 2. Whether the previous s[i-1] and p[j] match, and whether the newly added s[i-1] is equal to the characters before *
else if(dp[i - 1][j] && s.charAt(i - 1) == p.charAt(j - 2))
dp[i][j] = true;
// 3. Whether the first s[i-1] and p[j] match and whether the character before * is'. '
else if(dp[i - 1][j] && p.charAt(j - 2) == '.')
dp[i][j] = true;
} else {
// 1. Does the previous s[i-1] match p[j-1], and s[i-1] == p[i-1]
if(dp[i - 1][j - 1] && s.charAt(i - 1) == p.charAt(j - 1))
dp[i][j] = true;
// 2. Whether the previous s[i-1] matches p[j-1], and s[i-1] = = '
else if(dp[i - 1][j - 1] && p.charAt(j - 1) == '.')
dp[i][j] = true;
}
}
}
return dp[m - 1][n - 1];
}
}
4. Sword finger Offer 42. Maximum sum of continuous subarrays [easy]
Go and do the problem
Enter an integer array. One or more consecutive integers in the array form a sub array. Find the maximum value of the sum of all subarrays.
The required time complexity is O(n).
Input: num = [- 2,1, - 3,4, - 1,2,1, - 5,4]
Output: 6
- dp[i] represents the maximum sum of subarrays ending in num [i]
- dp[0] = dp[0]
DP [i] = max (maximum sum of subarrays ending with nums[i-1] + nums[i], nums[i]) - As long as the maximum value is returned, there is no need to find all the States and open up the array space.

class Solution {
public int maxSubArray(int[] nums) {
// pre = maximum sum of subarrays ending in x
// maxAns = maximum sum
int pre = 0, maxAns = nums[0];
for (int x : nums) {
pre = Math.max(pre + x, x);
maxAns = Math.max(maxAns, pre);
}
return maxAns;
}
}
5. Sword finger Offer 46. Translate numbers into strings [medium]
Go and do the problem
Given a number, we translate it into a string according to the following rules: 0 into "a", 1 into "b",..., 11 into "l",..., 25 into "z". A number may have multiple translations. Please program a function to calculate how many different translation methods there are for a number.
Input: 12258
Output: 5
Explanation: 12258 has five different translations, namely "bccfi", "bwfi", "bczi", "mcfi" and "mzi"
For the special step jumping problem, the difference is whether you can jump two steps or not.
- dp[i] represents the number of schemes for the translation of prefix strings ending in bit I. consider the contribution of bit I to dp[i] by translating alone and connecting with the previous bit
- dp[0] = 1
- dp[i] = dp[i-1] + dp[i-2] (10<x<25)|| dp[i-1]
//The code is similar to 2. Frog jumping steps, except that judgment 10 < x < 25 is added
class Solution {
public int translateNum(int num) {
//String.valueOf() converts [int num] into a string
String src = String.valueOf(num);
int f0 = 1, f1 = 1;
int fn = 1;
for (int i = 1; i < src.length(); i++) {
// string.substring(from, to)
// from: the position of the first character of the extracted substring.
// To: 1 more than the last character position of the substring to be extracted. If there is no this parameter, it will be intercepted to the end of the string
String subS = src.substring(i - 1, i + 1);
//judge
// compareTo: if the string is less than the string parameter, a value less than 0 will be returned; If the string is greater than the string parameter, a value greater than 0 is returned.
if(subS.compareTo("25") <= 0 && subS.compareTo("10") >= 0){
fn = f0 + f1;
}else{
fn = f1;
}
f0 = f1;
f1 = fn;
}
return fn;
}
}
6. Sword finger Offer 47. Maximum value of gift [medium]
Go and do the problem
There is a gift in each grid of an m*n chessboard, and each gift has a certain value (value greater than 0). You can start from the upper left corner of the chessboard to take the gifts in the grid, and move one grid to the right or down at a time until you reach the lower right corner of the chessboard. Given the value of a chessboard and the gifts on it, please calculate the maximum value of gifts you can get?
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Input: 12
After all traversal, the maximum value is returned
- DP [i] [j] represents the maximum value that can be obtained when reaching (I, j).
- dp[0][0] = grid[0][0]
- dp[ i ][ j ] = grid[ i ][ j ] + max(dp[i-1][j],dp[i][j-1])
- Because you can only go down or right, when you reach a new grid, it depends on whether the value from the top (i-1, j) is greater or the value from the left (i, j-1). Also note that there is no (i-1, j) in the first row and no (i, j-1) in the first column.
class Solution {
public int maxValue(int[][] grid) {
int m = grid.length, n = grid[0].length;
// First row and first column assignment
// The accumulated value is directly assigned to grid[i][j], without defining another dp [] []
for(int i=1; i<m; i++)
grid[i][0] += grid[i-1][0];
for(int j=1; j<n; j++)
grid[0][j] += grid[0][j-1];
// Traverse the chessboard
for(int i=1; i<m; i++){
for(int j=1; j<n; j++){
// Take the larger of the two and add up with the original value
grid[i][j] += Math.max(grid[i-1][j], grid[i][j-1]);
}
}
return grid[m-1][n-1];
}
}
7. Sword finger Offer 48. Longest substring without duplicate characters [medium]
Go and do the problem
Please find the longest substring that does not contain duplicate characters from the string and calculate the length of the longest substring.
Enter: "abcabcbb"
Output: 3
- dp[j] represents the length of the "longest non repeating substring" ending with the character s[j]
- dp[0] = 1
- dp[j] = dp[j-1] + 1 (character s[i] is outside the substring dp[j − 1] interval) | j - i (character s[i] is in the substring dp[j-1] interval)
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> dic = new HashMap<>();
// res = maximum length
// tmp = length of currently non repeating substring
int res = 0, tmp = 0;
for(int j = 0; j < s.length(); j++) {
// Get index i
// The getOrDefault() method obtains the value corresponding to the specified key pair. If the key is not found, the set default value is returned.
// charAt() returns the character at the specified position in the string
int i = dic.getOrDefault(s.charAt(j), -1);
// Use the hash table to count the index position of the last occurrence of each character
dic.put(s.charAt(j), j);
// j traverses straight ahead, i = the index position of the last occurrence s[j]. If it is the first occurrence, it is equal to - 1
// j-i = length between two identical letters
// ① tmp = tmp+1 [TMP < J - I] character s[i] is outside the substring dp[j − 1] interval
// ② tmp = j-i [TMP > J - I] character s[i] is in the substring dp[j-1] interval
tmp = tmp < j - i ? tmp + 1 : j - i;
// max(dp[j - 1], dp[j])
res = Math.max(res, tmp);
}
return res;
}
}
8. Sword finger Offer 49. Ugly number [medium]
Go and do the problem
We call numbers containing only qualitative factors 2, 3 and 5 ugly numbers. Find the nth Ugly Number in the order from small to large.
Input: n = 10
Output: 12
- dp[n] represents the nth-1st ugly number
- dp[0] = 1
dp[1] = 2 - dp[i] = min(?×2,?×3,?×5)
- An ugly number × 2. 3 and 5 will produce a new ugly number. The new ugly number in the ugly number array from small to large should be equal to the old ugly number × 2. 3 and 5 generate three numbers, and then compare the size to obtain.
- Three pointers are used to indicate whether the ugly number at this time is correct × 2,3,5
class Solution {
public int nthUglyNumber(int n) {
//initialization
int[] dp = new int[n];
dp[0] = 1;
//With three pointers
int p2 = 0, p3 = 0, p5 = 0;
//Each cycle calculates an ugly number and assigns it to dp[n]
for (int i = 1; i < n; i++) {
//Initially, all three pointers point to dp[0]. If this number is added to the array, the corresponding pointer will++
int num2 = dp[p2] * 2,
num3 = dp[p3] * 3,
num5 = dp[p5] * 5;
dp[i] = Math.min(Math.min(num2, num3), num5);
if (dp[i] == num2) p2++;
if (dp[i] == num3) p3++;
if (dp[i] == num5) p5++;
}
return dp[n-1];
}
}
9. Sword finger offer 60. Points of N dice [medium]
Go and do the problem
Throw n dice on the ground, and the sum of points on the upward side of all dice is s. Enter n to print out the probability of occurrence of all possible values of S.
You need to use an array of floating-point numbers to return the answer, in which the i-th element represents the probability of the i-th smallest in the set of points that the n dice can roll.
Input: 1
Output: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
- The probability of occurrence of the sum of all points shall be printed. So how many numbers should there be in the output array? There are 6n-(n-1) = 5n+1. [with the increase of N, the maximum number that can appear is 6n, and then subtract n-1 (if 6 dice are thrown on the ground, the minimum number is 6, that is, 6 1, which cannot appear [1, 2, 3, 4, 5], so the sum that can appear should be subtracted from n-1]
- dp[n] represents the probability of all possible values of N dice
- dp[1] = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6]
- Probability of the corresponding sum in dp[n] array = the probability that the original sum is + the probability that the new combination can be the sum
Take n=2 as an example
Find dp[2] and the influence of the probability of traversing each point of dp[1] on dp[2] array.
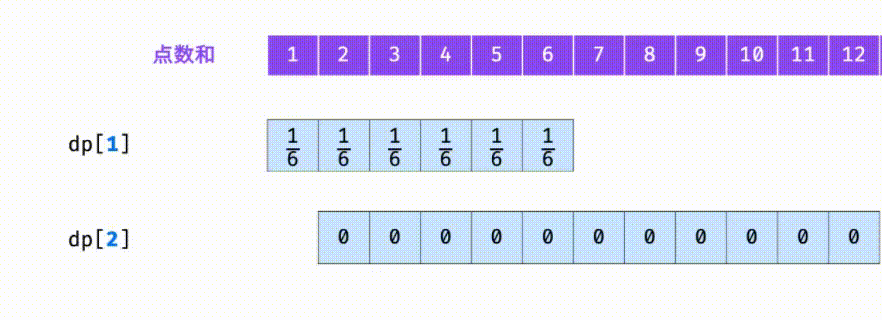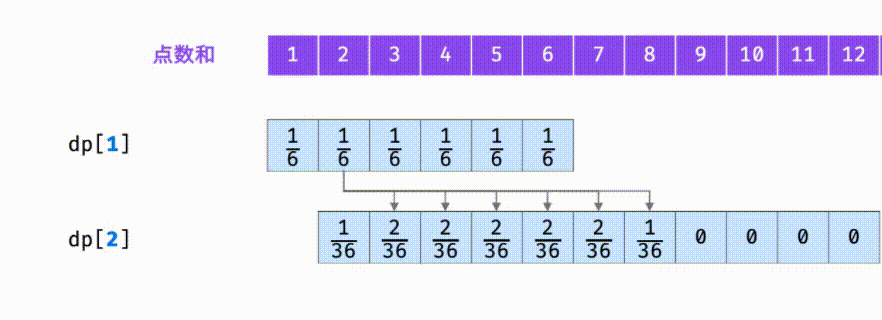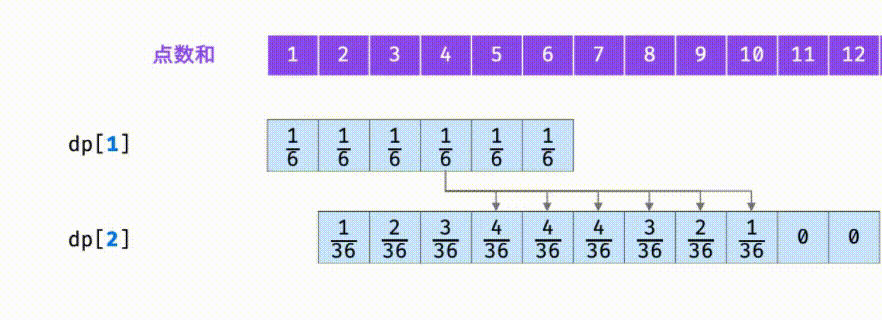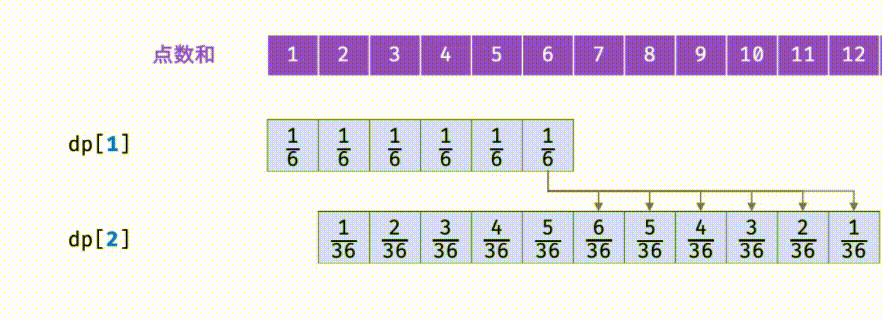
Figure from: Solution to the Krahets problem
class Solution {
public double[] dicesProbability(int n) {
// dp initialization, a dice value is all 1 / 6
double[] dp = new double[6];
Arrays.fill(dp, 1.0 / 6.0);
// Loop until n dice are found
for (int i = 2; i <= n; i++) {
double[] tmp = new double[5 * i + 1];
// Traverse DP array, J < dp.length
for (int j = 0; j < dp.length; j++) {
for (int k = 0; k < 6; k++) {
// The new dice may throw values of [1 ~ 6], which will affect the original dp array.
tmp[j + k] = tmp[j + k] + dp[j] *(1.0/6.0);
}
}
//dp and tmp are assigned alternately, tmp is the current demand, dp is n-1, and finally tmp is assigned to dp
dp = tmp;
}
return dp;
}
}
10. Sword finger Offer 63. Maximum profit of stock [medium]
Go and do the problem
Suppose the price of a stock is stored in the array in chronological order, what is the maximum profit that can be obtained from buying and selling the stock at one time?
You can only choose to buy this stock one day and sell it on a different day in the future.
Input: [7,1,5,3,6,4]
Output: 5
- Define status array dp
dp[i] represents the maximum profit of the subarray ending with prices[i] (that is, the maximum profit of the previous I days) - dp[0] = 0
DP [i] = max (the maximum profit of the previous (i-1) day, the i-day-the lowest price of the previous I day) - Because you only need to get the maximum profit, you don't need to store all the States. You can use the idea of rolling array to optimize the space.
class Solution {
public int maxProfit(int[] prices) {
//cost = lowest price in the previous i day
//Profit = maximum profit
int cost = Integer.MAX_VALUE, profit = 0;
for(int price : prices) {
cost = Math.min(cost, price);
profit = Math.max(profit, price - cost);
}
return profit;
}
}
Thank you for reading and like it 😉😉