What is bubble sorting

Bubble Sort is the most basic exchange sort.
Everyone must have drunk soda. There are often many small bubbles floating on it. This is because the carbon dioxide that makes up small bubbles is lighter than water, so small bubbles can float upward bit by bit.
The basic idea of Bubble Sorting is to compare the values of adjacent elements from front to back (starting from the elements with smaller subscripts) through the sequence to be sorted, and exchange them if the reverse order is found, so that the elements with larger values gradually move from front to back, just like bubbles under the water.

Examples demonstrating the bubbling process (illustration)

Summarize the process illustrated above:
(1) The size of the array is - 1 large cycle
(2) The number of times of each sorting is gradually decreasing
(3) If we find that there is no exchange in a certain sort, we can end the bubble sort in advance. This is optimization

Bubble sort first edition

#include <iostream>
#include <string>
using namespace std;
/*Array traversal*/
void ListShow(int list[], int length)

{
	for (int i = 0; i < length; i++)
	{
		cout << list[i] << "  ";
	}
	cout << endl;
}
/*==================Bubble sorting==========================*/
void BubbleSort(int *list, int length)
{
	int temp; //Define intermediate variables
	cout << "====Bubble sorting=====" << endl;
	for (int i = 0; i < length - 1; i++)
	{ //The length of the array is n, and the bubble sorting comparison is n-1 times
		//In each trip, the data are compared in pairs, and the large ones move back
		for (int j = 0; j < length - i - 1; j++)
		{
			if (list[j] > list[j + 1])
			{ //Exchange, from small to large, if > from large to small
				temp = list[j];
				list[j] = list[j + 1];
				list[j + 1] = temp;
			}
		}
		cout << "The first" << i + 1 << "Trip: ";
		ListShow(list, length);
	}
}
int main()
{
	int list[9] = {9, 3, 1, 4, 2, 7, 8, 6, 5};
	int length = sizeof(list) / sizeof(list[0]); //Find the length of the array, fixed in C + +
	cout << "Before sorting" << endl;
	ListShow(list, length);
	BubbleSort(list, length);
	cout << "After sorting" << endl;
	ListShow(list, length);
	return 0;
}

Bubble sort Second Edition

This version of the code has made small changes, using the boolean variable flag as a marker. If the elements are exchanged in this round of sorting, the sequence is out of order; If there is no element exchange, it means that the sequence is already in order and directly jumps out of the big cycle.

#Include < iostream > / / bubble optimization version 2 solves the problem of overall order
#include <string>
using namespace std;
void listshow(int list[], int length)
{
	for (int i = 0; i < length; i++)
	{
		cout << list[i] << "  ";
	}
	cout << endl;
}
void bubblesort(int array[], int length)
{
	int temp;
	for (int i = 0; i < length - 1; i++)
	{
		bool flage = true;
		for (int j = 0; j < length - i - 1; j++)
		{
			if (array[j] > array[j + 1])
			{
				temp = array[j];
				array[j] = array[j + 1];
				array[j + 1] = temp;
				flage = false;
			}
		}
		if (flage)
		{
			break;
		}
		else
		{
			cout << "The first" << i + 1 << "second" << endl;
			listshow(array, length);
		}
	}
}

int main()
{
	int a[7] = {3, 4, 1, 5, 6, 7, 8};
	int b = sizeof(a) / sizeof(a[0]);
	cout << "Before sorting" << endl;
	listshow(a, b);
	bubblesort(a, b);
	cout << "After sorting" << endl;
	listshow(a, b);
}

Bubble sorting Third Edition

To illustrate this problem, we re select a new sequence:
3 4 2 1 5 6 7 8
The characteristic of this sequence is that the first half (3, 4, 2, 1) is disordered, the second half (5, 6, 7, 8) is ascending, and the second half
The element of is already the maximum value of the sequence.
Let's sort according to the idea of bubble sorting to see the specific effect:
first round
Comparing elements 3 and 4, it is found that 3 is less than 4, so the position remains unchanged.
Comparing elements 4 and 2, it is found that 4 is greater than 2, so 4 and 2 exchange.
Comparing elements 4 and 1, it is found that 4 is greater than 1, so 4 and 1 exchange.
Comparing elements 4 and 5, it is found that 4 is less than 5, so the position remains unchanged.
Comparing elements 5 and 6, it is found that 5 is less than 6, so the position remains unchanged.
Comparing elements 6 and 7, it is found that 6 is less than 7, so the position remains unchanged.
Comparing elements 6 and 7, it is found that 6 is less than 7, so the position remains unchanged.
At the end of the first round, the sequence ordered area contains one element: 3 2 1 4 5 6 7 8
Second round
Comparing elements 3 and 2, it is found that 3 is greater than 2, so 3 and 2 exchange.
Comparing elements 3 and 4, it is found that 3 is less than 4, so the position remains unchanged.
Comparing elements 4 and 5, it is found that 4 is less than 5, so the position remains unchanged.
Comparing elements 5 and 6, it is found that 5 is less than 6, so the position remains unchanged.
Comparing elements 6 and 7, it is found that 6 is less than 7, so the position remains unchanged.
Comparing elements 7 and 8, it is found that 7 is less than 8, so the position remains unchanged.
At the end of the second round, the sequence ordered area contains one element: 2 1 3 4 5 6 7 8

Where is the key point of this problem? The key is to define the ordered region of the sequence.
According to the existing logic, the length of the ordered area is equal to the number of rounds of sorting. For example, the length of the ordered area after the first round of sorting is 1, and the length of the ordered area after the second round of sorting is 2
In fact, the real ordered area of the sequence may be larger than this length. For example, in the second round, the last five elements actually belong to the ordered area. Therefore, many subsequent element comparisons are meaningless.
How to avoid this situation? At the end of each round of sorting, we can record the position of the last element exchange, which is the boundary of the unordered sequence, and then the ordered area.

#Include < iostream > / / the third edition of bubble optimization, and the later parts have been ordered
#include <string>
using namespace std;
void ListShow(int list[], int length)
{
	for (int i = 0; i < length; i++)
	{
		cout << list[i] << "  ";
	}
	cout << endl;
}
void BubbleSort(int array[], int length)
{
	int t;
	int lastchange = 0; //Record the location of the last exchange
	for (int i = 0; i < length - 1; i++)
	{
		bool flage = true;				//The initial value of each round is true
		int sortbuder = length - i - 1; //For the boundary of unordered sequence, each comparison only needs to be compared so far
		for (int j = 0; j < sortbuder; j++)
		{
			if (array[j] > array[j + 1])
			{
				t = array[j];
				array[j] = array[j + 1];
				array[j + 1] = t;
				flage = false;		//There is element exchange, so it is not ordered, and the tag becomes false
				lastchange = j + 1; //Update the boundary of the unordered sequence to the position of the last exchange element
			}
		}
		if (flage)
		{
			break;
		}
		else
		{
			cout << "The first" << i + 1 << "second" << endl;
			sortbuder = lastchange;
			ListShow(array, length);
		}
	}
}
int main()
{
	int a[] = {1, 44, 4, 5, 64, 34, 35, 36, 39};
	int b = sizeof(a) / sizeof(a[0]);
	cout<<"Before sorting"<<endl;
	ListShow(a, b);
	BubbleSort(a, b);
	cout<<"After sorting"<<endl;
	ListShow(a, b);
}

In this version of code, sortBorder is the boundary of unordered sequence. In each round of sorting, the elements after sortBorder do not need to be compared at all. They must be orderly.

Bubble sorting Fourth Edition (cocktail sorting)

The element comparison and exchange process of cocktail sorting is two-way.
Let's take a chestnut:

There are 8 numbers to form an unordered sequence: 2, 3, 4, 5, 6, 7, 8, 1. I hope to sort from small to large
If you follow the idea of bubble sorting, what is the sorting process like?

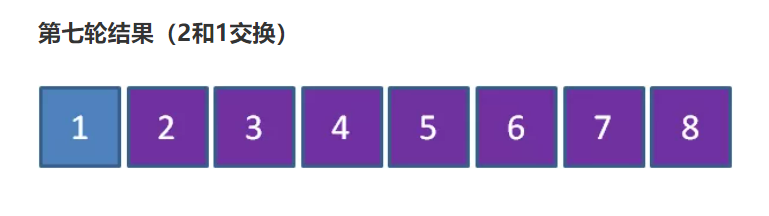
It can be seen that from 2 to 8 is already in order. Only the position of 1 element is wrong. There are seven rounds of sorting for lack. Is this too oppressive?
Cocktail sorting is to solve this problem

Detailed process of cocktail

First round (same as bubble sort, 8 and 1 exchange)

Second round
It's different now. We compare and exchange from right to left:
8 is already in the ordered area. Let's ignore 8 and compare 1 with 7. Element 1 is less than 7, so 1 and 7 exchange positions:

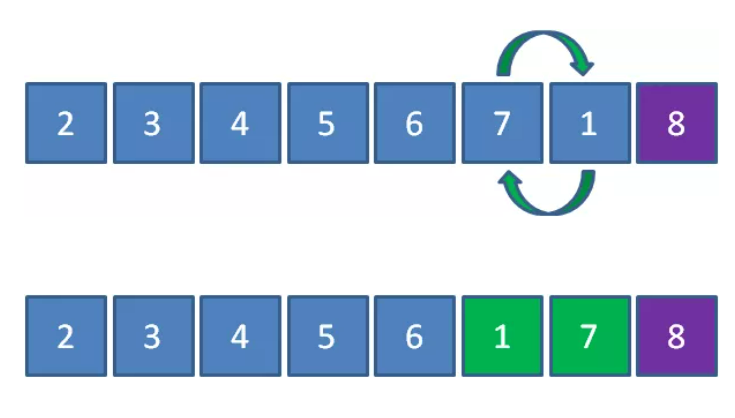
Next, comparing 1 and 6, element 1 is less than 6, so 1 and 6 exchange positions

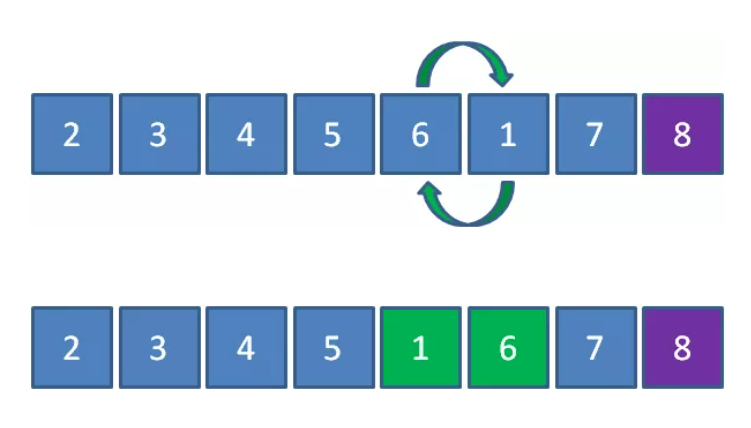
Next, comparing 1 and 5, element 1 is less than 5, so 1 and 5 exchange positions:

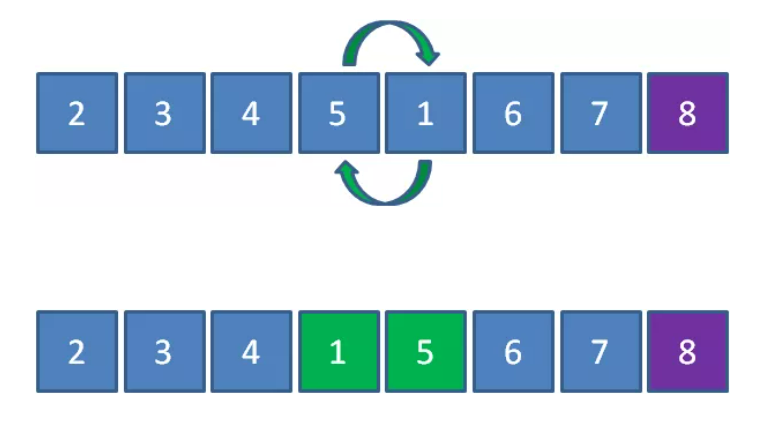
Next, 1 and 4 are exchanged, 1 and 3 are exchanged, and 1 and 2 are exchanged. Finally, the following results are obtained:

The third round (although it has been orderly, the process is not over)
The third round of cocktail sorting needs to be compared and exchanged from left to right:
Compared with 1 and 2, the position remains unchanged; Compared with 2 and 3, the position remains unchanged; Comparing 3 and 4, the position remains unchanged... Comparing 6 and 7, the position remains unchanged.
There is no element position exchange, which proves that it has been ordered and the sorting is over.

This is the idea of cocktail sorting. The sorting process is like a pendulum. The first round is from left to right, the second round is from right to left, and the third round is from left to right

#Include < iostream > / / cocktail sorting, first from left to right, then from right to left
#include <string>
using namespace std;
void ListShow(int list[], int length)
{
	for (int i = 0; i < length; i++)
	{
		cout << list[i] << "  ";
	}
	cout << endl;
}
void BubbleSort(int array[], int length)
{
	int t;
	for (int i = 0; i < length / 2; i++) //Because of the left and right sorting, you only need to sort by half
	{
		cout << "The first" << i + 1 << "Trip" << endl;
		//Odd wheel, compare and exchange from left to right
		bool flage = true;
		for (int j = 0; j < length - i - 1; j++)
		{
			if (array[j] > array[j + 1])
			{
				t = array[j];
				array[j] = array[j + 1];
				array[j + 1] = t;
				flage = false;
			}
		}

		if (flage)
		{
			break;
		}
		else
		{
			cout << "From left to right" << i + 1 << "second" << endl;
			ListShow(array, length);
		}
		//Re mark as true before even rounds
		flage = true;
		//Even wheel, compare and exchange from right to left
		for (int j = length - i - 1; j > i; j--)
		{
			if (array[j] < array[j - 1])
			{
				t = array[j];
				array[j] = array[j - 1];
				array[j - 1] = t;
				flage = false;
			}
		}
		if (flage)
		{
			break;
		}
		else
		{
			cout << "From right to left" << i + 1 << "second" << endl;
			ListShow(array, length);
		}
	}
}
int main()
{
	int a[] = {2, 3, 4, 5, 6, 7, 1, 8};
	int b = sizeof(a) / sizeof(a[0]);
	cout << "Before sorting" << endl;
	ListShow(a, b);
	BubbleSort(a, b);
	cout << "After sorting" << endl;
	ListShow(a, b);
}

This code is the original implementation of cocktail sorting. The large loop in the outer layer of the code controls all sorting rounds. The large loop contains two small loops. The first loop compares and exchanges elements from left to right, and the second loop compares and exchanges elements from right to left.

Bubble sorting Fifth Edition

Optimization of cocktail sorting

For one-way bubble sorting, we need to set a boundary value, and for two-way cocktail sorting, we need to set two boundary values. See code:

#Include < iostream > / / cocktail sorting Optimization: first from left to right, then from right to left
using namespace std;
void ListShow(int list[], int length)
{
	for (int i = 0; i < length; i++)
	{
		cout << list[i] << "  ";
	}
	cout << endl;
}
void BubbleSort(int array[], int length)
{
	int LastRightExchange = 0; //Record the position of the last exchange on the right
	int LastLeftExchange = 0;  //Record the position of the last exchange on the left
	int LeftSortBorder = 0;	   //The left boundary of the unordered sequence. Each comparison only needs to be compared so far
	int RightSortBorder;	   //The right boundary of the unordered sequence. Each comparison only needs to be compared so far
	int t;
	for (int i = 0; i < length / 2; i++) //Because of the left and right sorting, you only need to sort by half
	{
		cout << "The first" << i + 1 << "Trip" << endl;
		bool flage = true; //The initial value of each round is true
		RightSortBorder = length - i - 1;
		//Odd wheel, compare and exchange from left to right
		for (int j = LeftSortBorder; j < RightSortBorder; j++)
		{
			if (array[j] > array[j + 1])
			{
				t = array[j];
				array[j] = array[j + 1];
				array[j + 1] = t;
				flage = false;
				LastRightExchange = j + 1;
			}
		}
		RightSortBorder = LastRightExchange;
		if (flage)
		{
			break;
		}
		else
		{
			cout << "From left to right" << i + 1 << "second" << endl;
			ListShow(array, length);
		}
		//Re mark as true before even rounds
		flage = true;
		//Even wheel, compare and exchange from right to left
		for (int j = RightSortBorder; j > LeftSortBorder; j--)
		{
			if (array[j] < array[j - 1])
			{
				t = array[j];
				array[j] = array[j - 1];
				array[j - 1] = t;
				flage = false;
				LastLeftExchange = j - 1;
			}
		}
		LeftSortBorder = LastLeftExchange;
		if (flage)
		{
			break;
		}
		else
		{
			cout << "From right to left" << i + 1 << "second" << endl;
			ListShow(array, length);
		}
	}
}
int main()
{
	int a[] = {2, 3, 4, 5, 6, 7, 1, 8};
	int b = sizeof(a) / sizeof(a[0]);
	cout << "Before sorting" << endl;
	ListShow(a, b);
	BubbleSort(a, b);
	cout << "After sorting" << endl;
	ListShow(a, b);
}