2017-11-23 22:41

According to the derivation in the previous article, let the x-th neuron in the l(n) layer be l(n) (x) and its error value be delta ﹤ l(n) (x), then there is the following formula:
delta_l(n)_(x) = delta_l(n+1) * w(n+1) * f'(netl(n)_(x))
Where f '(NETL (n) UU (x)) is the derivative of the Delta (n) UU (x) activation function of neurons, and w(n+1) is the weight matrix of the link between Delta (n) UU (x) and delta (n).
For the derivation of bias b(n) of l(n) layer network, the formula is as follows:
d b(n)=sum( delta_l(n) )
Where sum is the summation function, which adds all the elements in the array Delta [u l (n).
According to this formula, a 6-layer neural network is constructed. Its structure is as follows: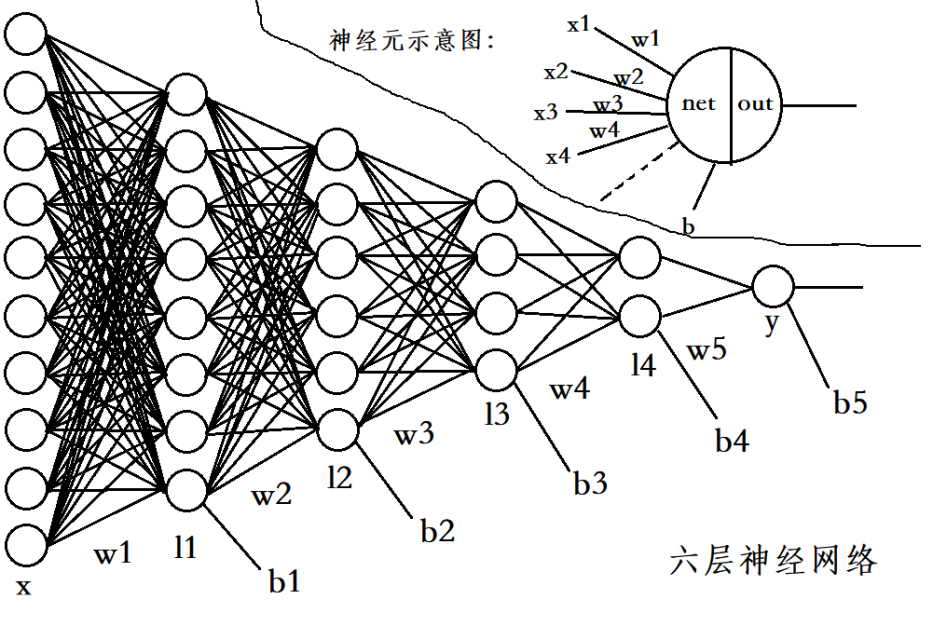
This design is purely for the sake of good-looking, and the number of neurons can be customized. From the figure, it can be seen that when the number of layers of neural network becomes more, the number of neurons is more, and the structure of this all connected neural network will become more complex, but it will reduce the efficiency of the network. Therefore, a convolutional neural network is proposed, which will not be discussed in this paper.
The implementation code of the above network is as follows:
 

'''*********************************************************************'''

import numpy as np


def f(x):

    return 1/(1+np.exp(-x))

def fd(a):

    return a*(1-a)

def run():

    x=np.array([0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1])

    y=0.25

    np.random.seed(1)

    w1=np.random.random((8,10))

    w2=np.random.random((6,8))

    w3=np.random.random((4,6))

    w4=np.random.random((2,4))

    w5=np.random.random((1,2))

    b1,b2,b3,b4,b5=0.2,0.3,0.4,0.5,0.6

    m=100

    alpha=0.9

    for i in range(m):

        netl1=np.array([np.sum(x*w1[0]),

                        np.sum(x*w1[1]),

                        np.sum(x*w1[2]),

                        np.sum(x*w1[3]),

                        np.sum(x*w1[4]),

                        np.sum(x*w1[5]),

                        np.sum(x*w1[6]),

                        np.sum(x*w1[7])])+b1

        outl1=f(netl1)

        netl2=np.array([np.sum(outl1[0]*w2[0]),

                        np.sum(outl1[1]*w2[1]),

                        np.sum(outl1[2]*w2[2]),

                        np.sum(outl1[3]*w2[3]),

                        np.sum(outl1[4]*w2[4]),

                        np.sum(outl1[5]*w2[5])])+b2

        outl2=f(netl2)

        netl3=np.array([np.sum(outl2[0]*w3[0]),

                        np.sum(outl2[1]*w3[1]),

                        np.sum(outl2[2]*w3[2]),

                        np.sum(outl2[3]*w3[3])])+b3

        outl3=f(netl3)

        netl4=np.array([np.sum(outl3[0]*w4[0]),

                        np.sum(outl3[1]*w4[1])])+b4

        outl4=f(netl4)

        nety=np.array([np.sum(outl4[0]*w5[0])])+b5

        outy=f(nety)

        #Total calculation error

        E=0.5*(y-outy)*(y-outy)

        #Back propagation

        delta_y=-(y-outy)*fd(outy)

        delta_l4=np.sum(delta_y*w5*fd(outl4))

        delta_l3=np.array([np.sum(delta_l4*w4.T[0])*fd(outl3[0]),

                           np.sum(delta_l4*w4.T[1])*fd(outl3[1]),

                           np.sum(delta_l4*w4.T[2])*fd(outl3[2]),

                           np.sum(delta_l4*w4.T[3])*fd(outl3[3])])

        delta_l2=np.array([np.sum(delta_l3*w3.T[0])*fd(outl2[0]),

                           np.sum(delta_l3*w3.T[1])*fd(outl2[1]),

                           np.sum(delta_l3*w3.T[2])*fd(outl2[2]),

                           np.sum(delta_l3*w3.T[3])*fd(outl2[3]),

                           np.sum(delta_l3*w3.T[4])*fd(outl2[4]),

                           np.sum(delta_l3*w3.T[5])*fd(outl2[5])])

        delta_l1=np.array([np.sum(delta_l2*w2.T[0])*fd(outl1[0]),

                           np.sum(delta_l2*w2.T[1])*fd(outl1[1]),

                           np.sum(delta_l2*w2.T[2])*fd(outl1[2]),

                           np.sum(delta_l2*w2.T[3])*fd(outl1[3]),

                           np.sum(delta_l2*w2.T[4])*fd(outl1[4]),

                           np.sum(delta_l2*w2.T[5])*fd(outl1[5]),

                           np.sum(delta_l2*w2.T[6])*fd(outl1[6]),

                           np.sum(delta_l2*w2.T[7])*fd(outl1[7])])

        dw1=np.array([delta_l1*x[0],

                      delta_l1*x[1],

                      delta_l1*x[2],

                      delta_l1*x[3],

                      delta_l1*x[4],

                      delta_l1*x[5],

                      delta_l1*x[6],

                      delta_l1*x[7],

                      delta_l1*x[8],

                      delta_l1*x[9]])

        w1-=alpha*dw1.T

        dw2=np.array([delta_l2*outl1[0],

                      delta_l2*outl1[1],

                      delta_l2*outl1[2],

                      delta_l2*outl1[3],

                      delta_l2*outl1[4],

                      delta_l2*outl1[5],

                      delta_l2*outl1[6],

                      delta_l2*outl1[7]])

        w2-=alpha*dw2.T

        dw3=np.array([delta_l3*outl2[0],

                      delta_l3*outl2[1],

                      delta_l3*outl2[2],

                      delta_l3*outl2[3],

                      delta_l3*outl2[4],

                      delta_l3*outl2[5]])

        w3-=alpha*dw3.T

        dw4=np.array([delta_l4*outl3[0],

                      delta_l4*outl3[1],

                      delta_l4*outl3[2],

                      delta_l4*outl3[3]])

        w4-=alpha*dw4.T


        dw5=np.array([delta_y*outl4[0],

                      delta_y*outl4[1]])

        w5-=alpha*dw5.T

    print(outy)

if __name__=='__main__':

    run()
'''*******************************************************************'''