introduction

Typhoon day, also practiced a day's car, Gan

[SUCTF2019]MT

To fill the hole
First look at the encryption code:

from Crypto.Util import number
from flag import flag

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) / 4):
        block = message[i * 4 : i * 4 +4]
        block = number.bytes_to_long(block)
        block = convert(block)
        block = number.long_to_bytes(block, 4)
        new_message += block
    return new_message

transformed_flag = transform(flag[5:-1].decode('hex')).encode('hex')
print 'transformed_flag:', transformed_flag
# transformed_flag: 641460a9e3953b1aaa21f3a2

Seeing this convert function, I was a little timid
This bit operation seems to completely disrupt the encrypted content (and I haven't done similar problems before)
Especially the second and third steps, I feel completely confused
Took a look Other people's wp , inspired
It is found that the last 9 bits of bin(2029229568) are all 0, while the last 17 bits (actually 18 bits) of bin(2245263360) are all 0, which is the same as the shifted bits
First of all, we should clarify one thing: the priority shift (> > and < < > and operation (&) > XOR operation (^) of bit operators
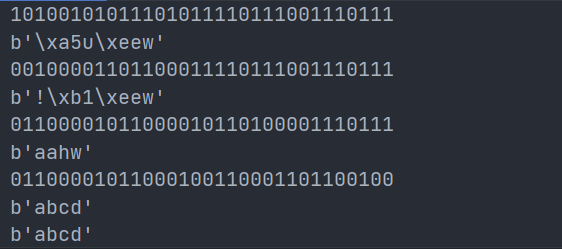
Take 'abcd' as an example to introduce the decryption process of the fourth and third steps (the first and second steps are the same)
Because I didn't install the environment of python2, I rewritten the encryption code with python3 and made a little modification
The code is as follows:

from Crypto.Util.number import *

flag = 'abcd'

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) // 4):
        block = message[i * 4: i * 4 + 4]
        block = bytes_to_long(block.encode())
        block = convert(block)
        block = bin(block)[2:].zfill(32)
        new_message += block
    return long_to_bytes(int(new_message, 2))

cipher = transform(flag)

Step 4 operation

First of all, you should know that "> >" means that the binary bit moves to the right, the low bit is discarded, and the high bit is supplemented by 0
The binary result after the first three steps of encryption is (of course, the following results are unknown during decryption):
10100101011101011110111001110111 is recorded as m4
Then the result of M4 > > 19 is
0000000000000000000101001010111 01011110111001110111
High complement 0 < -- > low discard
Next is the XOR operation
Two properties of XOR operation are required for decryption:
1. If a=b ^ c, then c=a ^ b
2,a=a ^ 0
Cipher = M4 ^ M4 > > 19, where cipher is known
In the process of bit-by-bit encryption, the first 19 bits of m4 are XOR with 0, that is, the first 19 bits of cipher are the same as m4, so the first 19 bits of m4 can be obtained
And because the last 13 bits of m4 ^ m4 > > 19 = the last 13 bits of m4 ^ the first 13 bits of m4 = the last 13 bits of cipher
So the last 13 bits of cipher ^ the first 13 bits of m4 = the last 13 bits of m4
Thus, the complete m4 can be obtained
The decryption code is as follows:

block = bytes_to_long((cipher[i * 4: i * 4 + 4]))
block = bin(block)[2:].zfill(32)
# step4 decode
m4 = block[:19] + bin(int(block[:13], 2) ^ int(block[19:], 2))[2:].zfill(13)
print(m4)
print(long_to_bytes(int(m4, 2)))

Step 3 operation

First of all, you should know that "< <" is that the binary bit moves to the left, the high bit is discarded, and the low bit is filled with 0; & " It is a bitwise and operation. There are 0 out of 0 and all 1 out of 1
The binary result after the first two steps of encryption is (of course, the following results are unknown during decryption):
001000010110001111101111001110111 is recorded as m3
00100001101100011 11011100111011100000000000000000
High discard < -- > low complement 0
Next is the sum operation
First, let's look at bin(2245263360) = '0b1000010110101000000000000000000000000000000'
It is found that the last 17 bits of 2245263360 are 0
Then, the last 17 digits of M3 < < 17 & the last 17 digits of 2245263360 = 00000000000000000 (17 zeros)
The same as the decryption operation in step 4, we can get that the last 17 bits of m3 are the last 17 bits of m4
And because the first 15 digits of M3 ^ m3 < < 17 & the first 15 digits of 2245263360 = the first 15 digits of M3 ^ the last 15 digits of M3 & the first 15 digits of 2245263360 = the first 15 digits of m4
Thus, the complete m3 can be obtained
The decryption code is as follows:

# step3 decode
block = m4
m3 = bin((int(block[17:], 2) & int(bin(2245263360)[2:].zfill(32)[:15], 2)) ^ int(block[:15], 2))[2:].zfill(15) + block[15:]
print(m3)
print(long_to_bytes(int(m3, 2)))

The second step is similar to the decryption in the first step, that is, it needs to be repeated several times
The complete test decryption code is as follows:

from Crypto.Util.number import *

flag = 'abcd'

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) // 4):
        block = message[i * 4: i * 4 + 4]
        block = bytes_to_long(block.encode())
        block = convert(block)
        block = bin(block)[2:].zfill(32)
        new_message += block
    return long_to_bytes(int(new_message, 2))

cipher = transform(flag)
print(bin(bytes_to_long(cipher))[2:].zfill(32))
print(cipher)
plain = ''
for i in range(len(cipher) // 4):
    block = bytes_to_long((cipher[i * 4: i * 4 + 4]))
    block = bin(block)[2:].zfill(32)
    # step4 decode
    m4 = block[:19] + bin(int(block[:13], 2) ^ int(block[19:], 2))[2:].zfill(13)
    print(m4)
    print(long_to_bytes(int(m4, 2)))
    # step3 decode
    block = m4
    m3 = bin((int(block[17:], 2) & int(bin(2245263360)[2:].zfill(32)[:15], 2)) ^ int(block[:15], 2))[2:].zfill(15) + block[15:]
    print(m3)
    print(long_to_bytes(int(m3, 2)))
    # step2 decode
    block = m3
    m2 = bin((int(block[23:], 2) & int(bin(2029229568)[2:].zfill(32)[14:23], 2)) ^ int(block[14:23], 2))[2:].zfill(9) + block[23:]
    block = m3[:14] + m2
    m2 = bin((int(block[14:23], 2) & int(bin(2029229568)[2:].zfill(32)[5:14], 2)) ^ int(block[5:14], 2))[2:].zfill(9) + block[14:]
    block = m3[:5] + m2
    m2 = bin((int(block[9:14], 2) & int(bin(2029229568)[2:].zfill(32)[:5], 2)) ^ int(block[:5], 2))[2:].zfill(5) + block[5:]
    print(m2)
    print(long_to_bytes(int(m2, 2)))
    # step1 decode
    block = m2
    m1 = block[:13] + bin(int(block[:13], 2) ^ int(block[13:26], 2))[2:].zfill(13)
    block = m1 + block[26:]
    m1 = block[:26] + bin(int(block[13:19], 2) ^ int(block[26:], 2))[2:].zfill(6)
    print(m1)
    print(long_to_bytes(int(m1, 2)))
    plain += m1
print(long_to_bytes(int(plain, 2)))

The result is right

Then the test decrypted code is applied to transformed_ On flag
There is a bit of trouble here, that is, the original encryption code needs another step: transformed_flag = transform(flag[5:-1].decode('hex')).encode('hex')
Python 3 does not have decode('hex ') and encode('hex'), which can be used for reference Conversion between Python 3 string and hex
. decode('hex ') corresponds to hex()，. encode('hex ') corresponds to bytes fromhex()
Therefore, the complete decryption code is as follows:

from Crypto.Util.number import *

cipher = bytes.fromhex('641460a9e3953b1aaa21f3a2')
print(cipher)
plain = ''
for i in range(len(cipher) // 4):
    block = bytes_to_long((cipher[i * 4: i * 4 + 4]))
    block = bin(block)[2:].zfill(32)
    # step4 decode
    m4 = block[:19] + bin(int(block[:13], 2) ^ int(block[19:], 2))[2:].zfill(13)
    print(m4)
    print(long_to_bytes(int(m4, 2)))
    # step3 decode
    block = m4
    m3 = bin((int(block[17:], 2) & int(bin(2245263360)[2:].zfill(32)[:15], 2)) ^ int(block[:15], 2))[2:].zfill(15) + block[15:]
    print(m3)
    print(long_to_bytes(int(m3, 2)))
    # step2 decode
    block = m3
    m2 = bin((int(block[23:], 2) & int(bin(2029229568)[2:].zfill(32)[14:23], 2)) ^ int(block[14:23], 2))[2:].zfill(9) + block[23:]
    block = m3[:14] + m2
    m2 = bin((int(block[14:23], 2) & int(bin(2029229568)[2:].zfill(32)[5:14], 2)) ^ int(block[5:14], 2))[2:].zfill(9) + block[14:]
    block = m3[:5] + m2
    m2 = bin((int(block[9:14], 2) & int(bin(2029229568)[2:].zfill(32)[:5], 2)) ^ int(block[:5], 2))[2:].zfill(5) + block[5:]
    print(m2)
    print(long_to_bytes(int(m2, 2)))
    # step1 decode
    block = m2
    m1 = block[:13] + bin(int(block[:13], 2) ^ int(block[13:26], 2))[2:].zfill(13)
    block = m1 + block[26:]
    m1 = block[:26] + bin(int(block[13:19], 2) ^ int(block[26:], 2))[2:].zfill(6)
    print(m1)
    print(long_to_bytes(int(m1, 2)))
    plain += m1
print(long_to_bytes(int(plain, 2)))
print(long_to_bytes(int(plain, 2)).hex())

The result is:

flag

An unimaginable path

As mentioned in wp, there is also a solution to get the result through repeated encryption
Here is the code of Python 3:

from Crypto.Util.number import *

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = b''
    for i in range(len(message) // 4):
        block = message[i * 4: i * 4 + 4]
        block = bytes_to_long(block)
        block = convert(block)
        block = long_to_bytes(block, 4)
        new_message += block
    return new_message

transformed_flag = '641460a9e3953b1aaa21f3a2'
cipher = bytes.fromhex('641460a9e3953b1aaa21f3a2')
# assert (transform(bytes.fromhex('84b45f89af22ce7e67275bdc')).hex() == transformed_flag)
c = cipher
s = set()
while True:
    c = transform(c.zfill(len(cipher)))
    print(c.hex())
    s.add(c.hex())
    print(len(s))
    if c.hex() == transformed_flag:
        break

As for why, it is because the encryption algorithm used in this problem is Mersenne twister , is a pseudo-random number generation algorithm. An updated and more commonly used algorithm of this algorithm is MT19937, 32-bit word length, corresponding to the problem
Moreover, the random number generated by the algorithm is periodic, which is not difficult to understand why the plaintext can be obtained by encrypting the ciphertext all the time, because the ciphertext is still obtained after a cycle, so the last one is plaintext
The result of the above decryption code is:

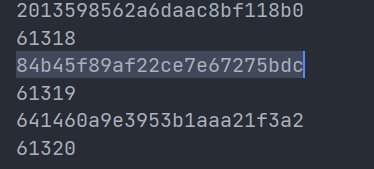
It is not difficult to find that its cycle is 61319

For more information about the shape of MT19937 pseudo-random number generation algorithm, please refer to the previous generation of madmonkey Analysis of mt19937 pseudo-random number generation algorithm
It introduces the same solution as the first method, but uses modular code like wp to package the decryption steps into functions
Here is the decryption code referring to the code therein:

from Crypto.Util.number import *

# right shift inverse
def inverse_right(res, shift, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift
    return tmp


# right shift with mask inverse
def inverse_right_mask(res, shift, mask, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift & mask
    return tmp

# left shift inverse
def inverse_left(res, shift, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift
    return tmp


# left shift with mask inverse
def inverse_left_mask(res, shift, mask, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift & mask
    return tmp


def extract_number(y):
    y = y ^ y >> 11
    y = y ^ y << 7 & 2636928640
    y = y ^ y << 15 & 4022730752
    y = y ^ y >> 18
    return y & 0xffffffff

def recover(y):
    y = inverse_right(y, 19)
    y = inverse_left_mask(y, 17, 2245263360)
    y = inverse_left_mask(y, 9, 2029229568)
    y = inverse_right(y, 13)
    return y & 0xffffffff

transformed_flag = '641460a9e3953b1aaa21f3a2'
cipher = bytes.fromhex('641460a9e3953b1aaa21f3a2')
new_message = b''
for i in range(len(cipher) // 4):
    block = cipher[i * 4: i * 4 + 4]
    block = bytes_to_long(block)
    block = recover(block)
    block = long_to_bytes(block, 4)
    new_message += block
print(new_message.hex())

The results are the same:

Another method is the black box method, which regards the binary coding of ciphertext and plaintext as two vectors a , b a,b a. B. according to the encryption method, there is a linear relationship between the two vectors, that is, there is a square matrix M M M. Make a = M b a=Mb a=Mb
The specific linear relationship is as follows:

I don't understand this method very much. I'll talk about it later (slip away)

epilogue

I wrote a little yesterday (July 24), but I didn't finish it
Because there is a bug in the code of method 2, I can't solve it. Thank Phoenix for helping me change it
Today (July 25), we strive to add another issue
(you asked me why I went on July 23? I made up for it all day [doge])
Hope to continue to insist