Time Limit: 20 Sec Memory Limit: 256 MB
Submit: 1108 Solved: 433

Description

Given n n n n n n n n points on a plane, the cost from (x1,y1) to (x2,y2) is defined as min(|x1-x2|,|y1-y2|), and the minimum cost from point 1 to point n is calculated.

Input

The first line contains a positive integer n (2<=n<=200000) representing the number of points.

Next n rows, each containing two integers x[i],y i Represents the coordinates of each point in turn.

Output

An integer, the minimum cost.

Sample Input

5

2 2

1 1

4 5

7 1

6 7

Sample Output

2

Questions:

Obviously this is a shortest path solution, so let's consider a few points of this graph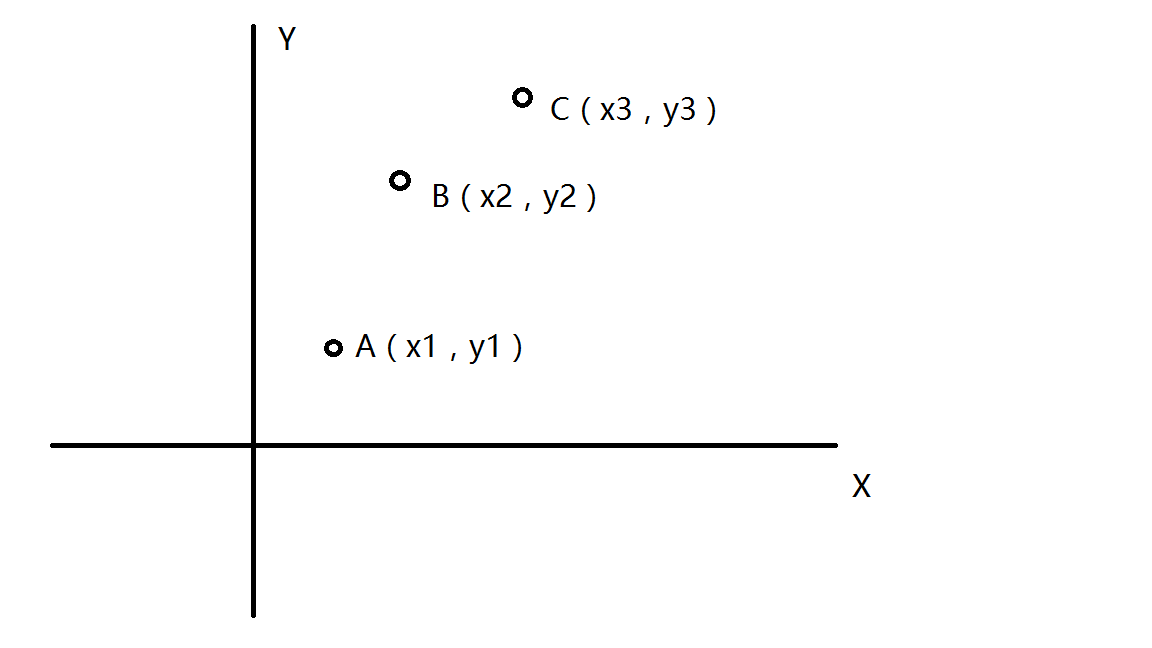

We will find that if we order points A, B and C by x, then we can't do a better job from A to C directly than from A to C, because in any case, I've already ranked them, and in the worst case, I choose to walk x every time, which is equivalent to the cost of walking x directly in the past. If I walk y every time, I walk directly in the past generation of Y.Prices are equivalent, so I can choose either X or y, so for X sorting, then adjacent edges (the reason why they are adjacent, from a to B and from B to C is already stated, because this is not inferior to A directly to C), for y sorting, edges in Y order can be built

Tip: 1 This card SPFA, so I used Dijkstra's stack to optimize the 2 this card burst int, to use long long long

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<queue>
#define ppap pair<long long,int>
const int MAXN=200000*2;
using namespace std;
int readin(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int head[MAXN],tail,n;
long long dis[MAXN];
bool vis[MAXN];
struct Point{int x,y,id;}p[MAXN];
struct Line{int from,to,num,nxt;}line[MAXN*2+10];
bool cmp(const Point &A,const Point &B){return A.x<B.x;}
bool cmpp(const Point &A,const Point &B){return A.y<B.y;}
void add_line(int from,int to,int num){tail++;line[tail].from=from;line[tail].to=to;line[tail].nxt=head[from];line[tail].num=num;head[from]=tail;}
void add(int a,int b,int num){add_line(a,b,num);add_line(b,a,num);}
void build(){
    sort(p+1,p+n+1,cmp);
    for(register int i=1;i<=n-1;i++) 
    add(p[i].id,p[i+1].id,p[i+1].x-p[i].x);
    sort(p+1,p+n+1,cmpp);
    for(register int i=1;i<=n-1;i++) 
    add(p[i].id,p[i+1].id,p[i+1].y-p[i].y);
}
void SPFA(){
    priority_queue<ppap,vector<ppap>,greater<ppap> >q;
    for(register int i=1;i<=n;i++) dis[i]=0x7fffffff;
    dis[1]=0;
    q.push(make_pair(0,1));
    while(!q.empty()){
        int u=q.top().second;q.pop();
        if(vis[u])continue; vis[u]=true;
        for(register int i=head[u];i;i=line[i].nxt){
            int v=line[i].to;
            if(dis[v]>dis[u]+line[i].num){
                dis[v]=dis[u]+line[i].num;
                q.push(make_pair(dis[v],v));
            }
        }
    }
    printf("%lld\n",dis[n]);
}
int main(){
    //freopen(".txt","r",stdin);
    //freopen(".out","w",stdout);
    n=readin();
    for(register int i=1;i<=n;i++){p[i].x=readin();p[i].y=readin();p[i].id=i;}
    build();
    SPFA();
    return 0;
}