E. Devoted Tomb Master
Topic Description
Xiao W is the administrator of a newly built cemetery. The cemetery can be seen as an N *M rectangle, each grid point of the rectangle, either planted with an evergreen tree, or a cemetery that has not yet belonged to. The local people are very devout Christians, and they are willing to find a suitable cemetery for themselves in advance. In order to show their sincerity to the Lord, they want their graveyard to have a high degree of piety. The devotion of a cemetery refers to the number of cross centered around the cemetery. A cross can be seen as a cemetery in the middle. There are exactly k evergreen trees on the top, bottom, left and right of the cemetery. Xiao W wants to know the total devotion of all the cemeteries in the cemetery he manages.
Input format
The first line contains two positive integers N and M separated by spaces, representing the width and length of the cemetery. Therefore, the rectangular cemetery has (N+1) x (M+1) grid points. The coordinates of the lower left corner are (0,0) and the upper right corner are (N,M). The second line contains a positive integer W, representing the number of evergreen trees in the cemetery. The third line consists of W rows, each containing two non-negative integers xi and yi separated by spaces, representing the coordinates of an evergreen tree. Input ensures that no two evergreen trees have the same coordinates. The last line contains a positive integer k, meaning as shown in the title.
Output format
It contains a non-negative integer that represents the total devotion of all the cemeteries in this cemetery. For convenience, the answer is 2,147,483,648.
Example
sample input
5 6 13 0 2 0 3 1 2 1 3 2 0 2 1 2 4 2 5 2 6 3 2 3 3 4 3 5 2 2
sample output
6
Data Scope and Tips
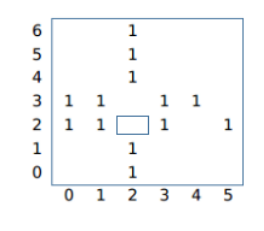
In the picture, there are three cross centered around the cemetery (2, 2) and (2, 3), that is to say, their piety is 3. The devotion of other cemeteries is 0. All data satisfy 1 < N, M < 1,000,000,000, 0 < xi < N, 0 < yi < M, 1 < W < 100,000, 1 < K < 10. There are 50% of the data, which satisfies 1 < K < 2. There are 25% of the data, satisfying 1 < W < 10000. Note: "There are exactly k trees." Here, instead of just having and only having, we choose k trees from the tree >= K.
Tree Array + Discrete + Combination Number
It's really a fairy question. The main reason is that the code is too messy (when it's discrete, it's necessary to hang up) and the test point is decadent before it's called out.
M, N is much bigger than W, iron must be discretized, then W2 can actually AC (data is a little water), but can be stuck off.
For a cemetery, if there are u[],d[],l[],r [] trees on the upper and lower sides, then his devotion is equal to C(u,k)*C(d,k)*C(l,k)*C(r,k).
For the space between two evergreen trees a and b in the same row, their l [] and r [] are the same, so we can consider using a tree array to maintain the prefix sum of C(u,k)*C(d,k) of each point in this row.
ans+=C(l[a]+1,k)*C(r[b]+1,k)*(ask(b-1)-ask(a)) can be changed at a single point when changing lines.
#include<map>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
#define mod 2147483648
#define ma(x) memset(x,0,sizeof(x))
using namespace std;
LL N,M,W,k;
LL C[100010][15];
LL xi[100010],yi[100010],tx[100010],ty[100010];
LL h[100010],l[100010];
LL ss[100010],xx[100010];
LL maxx,maxy;
vector<int> inc[100010];
LL Ch[100100];
int lowbit(int x){return x&(-x);}
void add(int x,LL y);
LL ask(int x);
void xget_C(int maxn);
signed main()
{
// freopen("25.in","r",stdin);
scanf("%lld%lld%lld",&N,&M,&W);
for(int i=1;i<=W;i++)scanf("%d%d",&xi[i],&yi[i]),tx[i]=xi[i],ty[i]=yi[i];
cin>>k;
xget_C(100000);
sort(xi+1,xi+W+1);
maxx=unique(xi+1,xi+W+1)-xi-1;
sort(yi+1,yi+W+1);
maxy=unique(yi+1,yi+W+1)-yi-1;
for(int i=1;i<=W;i++)
{
int t1=lower_bound(xi+1,xi+maxx+1,tx[i])-xi;
int t2=lower_bound(yi+1,yi+maxy+1,ty[i])-yi;
h[t2]++,l[t1]++;
inc[t2].push_back(t1);
}
for(int i=1;i<=maxy;i++)
sort(inc[i].begin(),inc[i].end());
for(int i=1;i<=maxx;i++)ss[i]=l[i];
LL ans=0;
for(int i=1;i<=maxy;i++)
{
for(int j=0;j<inc[i].size();j++)
{
ss[inc[i][j]]--,xx[inc[i][j]]++;
LL te1=(C[ss[inc[i][j]]][k]*C[xx[inc[i][j]]][k])%mod,
te2=(C[ss[inc[i][j]]+1][k]*C[xx[inc[i][j]]-1][k])%mod;
add(inc[i][j],(te1-te2+mod)%mod);
}
if(i>k && h[i]>=2*k)
for(int j=k;j+k<=inc[i].size();j++)
if(j && inc[i][j]!=inc[i][j-1]+1)
ans=(ans+C[j][k]*C[inc[i].size()-j][k]*(ask(inc[i][j]-1)-ask(inc[i][j-1])))%mod;
}
cout<<(ans%mod+mod)%mod<<endl;
}
void xget_C(int maxn)
{
C[0][0]=1;
for(int i=1;i<=maxn;i++)
{
C[i][0]=1;
for(int j=1;j<=min(i,11);j++)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
}
void add(int x,LL y)
{
while(x<=maxx)
{
Ch[x]=(Ch[x]+y)%mod;
x+=lowbit(x);
}
}
LL ask(int x)
{
LL ans=0;
while(x)
{
ans=(ans+Ch[x])%mod;
x-=lowbit(x);
}
return ans;
}