meaning of the title

The tree of $n $nodes can be divided into $\ frac{n}{k} $connection blocks with the size of $k $

Sol

First $k $must be a multiple of $n $.

Then at the beginning, I thought it was foolish to output all divisors..

But the picture is like this, if $k = 2 $, it is definitely not possible.

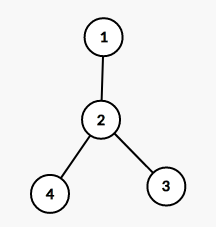
Conclusion: if $k $is feasible, there are at least $\ frac{n}{k} $nodes with multiple sizes of $k $

Proof: direct induction.

When $k = n $, it's obvious

When $k = n / 2 $, we should divide the tree into two disjoint blocks, which must be completely independent and have their own root nodes.

The rest can be summarized. Note why we are "at least" here, because the whole tree is connected. When we judge $k $, the size of $2k $, will also be counted into the answer

Then this question card dfs, worthy of SDOI..

#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int MAXN = 2 * 1e6;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int N;
vector<int> ap;
int fa[MAXN], tim[MAXN];
void rebuild() {
    memset(tim, 0, sizeof(tim));
   // for(int i = 1; i <= N; i++) v[i].clear();
    for(int i = 2; i <= N; i++) fa[i] = (fa[i] + 19940105) % (i - 1) + 1;
}
int siz[MAXN];
/*void dfs(int x, int fa) { mdzz Car dfs, it's SDOI.. 
    siz[x] = 1;
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa) continue;
        dfs(to, x);
        siz[x] += siz[to];
    }
}*/
void solve(int id) {
    printf("Case #%d:\n", id);
    for(int i = 1; i <= N; i++) siz[i] = 1;
    for(int i = N; i >= 1; i--) siz[fa[i]] += siz[i];
    for(int i = 1; i <= N; i++) tim[siz[i]]++;
    for(int i = 0; i < ap.size(); i++) {
        int num = ap[i], cnt = 0;
        for(int j = num; j <= N; j += num)
            cnt += tim[j];
        if(cnt >= N / num) {
            printf("%d\n", num);
        }
    }
}
int main() {
    N = read();
    for(int i = 1; i <= N; i++) 
        if(N % i == 0) 
            ap.push_back(i);
    for(int i = 2; i <= N; i++) 
        fa[i] = read();
    solve(1);
    for(int i = 2; i <= 10; i++) {
        rebuild();
        solve(i);
    }
    return 0;
}