catalogue
LR (first left single rotation and then right single rotation)
Rl (right single rotation first and then left single rotation)
3, Verification and deletion of AVL tree
AVL tree deletion (understand)
The bottom layers of associative container set/multiset and map/multimap are implemented according to binary search tree, but binary search tree itself has defects; If the inserted elements are ordered or approximately ordered, the binary search tree will degenerate into a single branch tree, and the actual complexity is O(N). Therefore, its underlying structure is balanced for the binary tree, that is, it is realized by using the balanced tree;
1, AVL tree
AVL tree concept
Binary search tree, if the data is ordered or approximately ordered, will degenerate into a single tree. Finding elements is equivalent to searching elements in the sequence table, which is inefficient; Therefore, Russian Mathematicians (G.M. Adelson velskii and E.M.Landis) invented a method to solve the above problem in 1962, that is, after inserting new nodes into the binary search tree, if the absolute value of the difference between the height of the left and right subtrees of each node can not exceed 1 (the nodes in the tree need to be adjusted), reduce the height of the tree, so as to reduce the average search length;
AVL tree (self balancing binary search tree): it is either an empty tree or an AVL tree with left and right subtrees, and the absolute value of the height difference between the left and right subtrees (referred to as the balance factor) does not exceed 1;
Balance factor BF(Balance Factor): the value of the height of the left subtree minus the height of the right subtree; The BF value range of the balanced binary tree is [- 1, 1]. If the BF value of a node exceeds the range, it needs to be adjusted;
- If a binary search tree is highly balanced, it is an AVL tree;
- AVL tree with n nodes, the height can be maintained at O(logN), and the search time complexity is O(logN);
Definition of AVL tree node
template <class T>
struct AVLTreeNode
{
AVLTreeNode(const T& data)
:_pLeft(nullptr)
,_pRight(nullptr)
,_pParent(nullptr)
,_data(data)
,_bf(0)
{}
AVLTreeNode<T>* _pLeft; //Left child of current node
AVLTreeNode<T>* _pRight; //Right child of the current node
AVLTreeNode<T>* _pParent; //Parent of current node
T _data;
int _bf; //Equilibrium factor
}AVL tree insertion
AVL tree introduces balance factor on the basis of binary search tree, which can also be regarded as binary search tree;
The AVL tree insertion process is divided into two steps:
- First, insert the new node in the way of binary search tree;
- Adjusting the balance factor of nodes;
2, Rotation of AVL tree
If a new node is inserted into a balanced AVL tree, resulting in imbalance, the structure needs to be adjusted to make it balanced;
According to the different insertion positions of nodes, the rotation of AVL tree can be divided into four types: LL (right single rotation), RR (left single rotation), LR (left single rotation first and then right single rotation), Rl (right single rotation first and then left single rotation);
Ll (right single rotation)
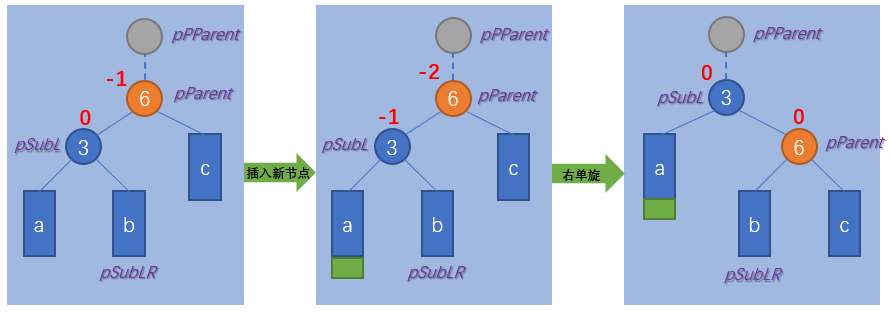
void _RotateR(pNode pParent)
{
pNode pSubL = pParent->_pLeft; //Parent left child
pNode pSubLR = pSubL->_pRight; //Parent left child's right child
pParent->_pLeft = pSubLR;
//If pSubLR exists
if (pSubLR)
pSubLR->_pParent = pParent;
pSubL->_pRight = pParent;
//If pParent may be a subtree, there are parent nodes
pNode pPParent = pParent->_pParent;
pParent->_pParent = pSubL;
pSubL->_pParent = pPParent;
if (pPParent == NULL)
{
_pRoot = pSubL;
pSubL->_pParent = NULL;
}
else
{
//pParent may be a left subtree or a right subtree
if (pPParent->_pLeft == pParent)
pPParent->_pLeft = pSubL;
else
pPParent->_pRight = pSubL;
}
//Update the balance factor of some nodes
pParent->_bf = pSubL->_bf = 0;
}RR (left single rotation)
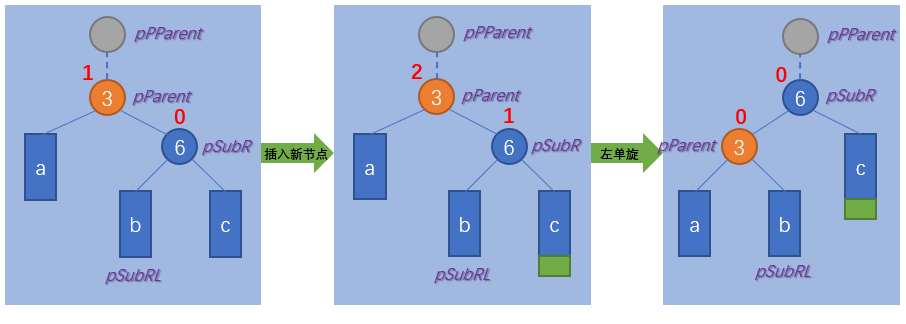
void _RotateL(pNode pParent)
{
pNode pSubR = pParent->_pRight; //pParent right child
pNode pSubRL = pSubR->_pLeft; //Parent left child of right child
pParent->_pRight = pSubRL;
//If pSubRL exists
if (pSubRL)
pSubRL->_pParent = pParent;
pSubR->_pLeft = pParent;
//If pParent may be a subtree, there are parent nodes
pNode pPParent = pParent->_pParent;
pParent->_pParent = pSubR;
pSubR->_pParent = pPParent;
if (pPParent == NULL)
{
_pRoot = pSubR;
pSubR->_pParent = NULL;
}
else
{
//pParent may be a left subtree or a right subtree
if (pPParent->_pLeft == pParent)
pPParent->_pLeft = pSubR;
else
pPParent->_pRight = pSubR;
}
//Update the balance factor of some nodes
pParent->_bf = pSubL->_bf = 0;
}LR (first left single rotation and then right single rotation)
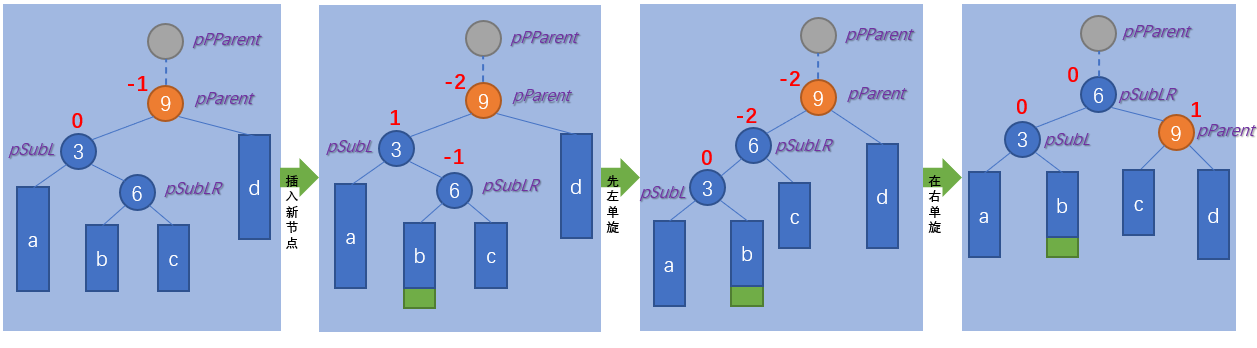
void _RotateLR(pNode pParent)
{
pNode pSubL = pParent->_pLeft;
pNode pSubLR = pSubL->_pRight;
int bf = pSubLR->_bf;
_RotateL(pParent->_pLeft);
_RotateR(pParent);
if (bf == 1)
pSubL->_bf = -1;
else if (bf == -1)
pParent->_bf = 1;
}Rl (right single rotation first and then left single rotation)
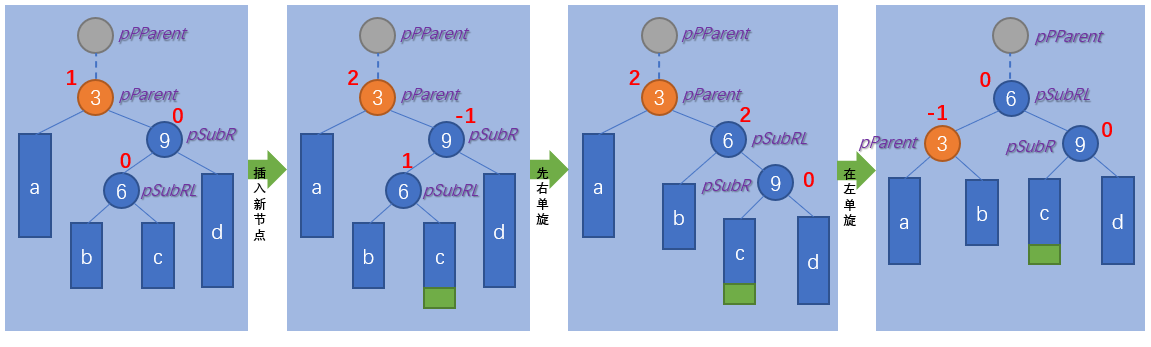
void _RotateLR(pNode pParent)
{
pNode pSubR = pParent->_pRight;
pNode pSubRL = pSubR->_pLeft;
int bf = pSubRL->_bf;
_RotateR(pParent->_pRight);
_RotateL(pParent);
if (bf == -1)
pSubR->_bf = 1;
else if (bf == 1)
pParent->_bf = -1;
}Note: the subtree whose parent is the root is unbalanced
- The balance factor of pParent is 2, indicating the height of the right subtree of pParent. Set the root of the right subtree as pSubR;
- The balance factor of single pSubR is 1, and left single rotation is performed;
- When the balance factor of single pSubR is - 1, execute the right single rotation first, and execute the left single rotation after the left single rotation;
- The balance factor of pParent is - 2, indicating the height of the left subtree of pParent. Set the root of the left subtree as pSubL;
- When the single pSubL balance factor is 1, execute the left single rotation first and the right single rotation later;
- The balance factor of single pSubL is - 1, and the right single rotation is executed;
After the rotation is completed, the height of the subtree with the original pParent as the root is reduced and has been balanced, so there is no need to update upward;
3, Verification and deletion of AVL tree
Verification of AVL tree
AVL tree adds balance restriction on the basis of binary search tree. To verify AVL tree, it can be divided into two steps;
- Verify that it is a binary search tree;
- If the middle order traversal obtains an ordered sequence, it is described as a binary search tree;
- Verify that it is a balanced tree;
- The absolute value of the height difference of each node subtree shall not exceed 1;
- Whether the balance factor of the node is calculated correctly;
int _Height(pNode pRoot);
bool _IsBalanceTree(pNode pRoot)
{
if (pRoot == nullptr)
return true;
int leftHeight = _Height(pRoot->_pLeft);
int rightHeight = _Height(pRoot->_pRight);
int diff = rightHeight - leftHeight;
if (diff != pRoot->_bf || (diff > 1 || diff < -1))
return false;
return _IsBalanceTree(pRoot->_pLeft) && _IsBalanceTree(pRoot->_pRight);
}AVL tree deletion (understand)
Because AVL tree is also a binary search tree, nodes can be deleted in the way of binary search tree.
Then, when updating the balance factor, the balance factor after deleting the node is updated. In the worst case, it has to be adjusted to the root node;
Note: refer to introduction to algorithm or data structure - description with object-oriented method and C + +;
4, Performance of AVL tree
- AVL tree is an absolutely balanced binary search tree, which requires that the absolute value of the height difference between the left and right subtrees of each node should not exceed 1, which can ensure efficient time complexity O(logN);
- However, if you want to modify the AVL tree, the performance is very low. For example, you need to maintain its absolute balance during insertion, and there are many rotations. What's worse, when deleting, the right may keep the rotation to the root position;
- Therefore, if a query efficient and orderly data structure is needed, and the number of data is static (i.e. it will not change), AVL tree can be considered, but it is not appropriate to modify a structure frequently;