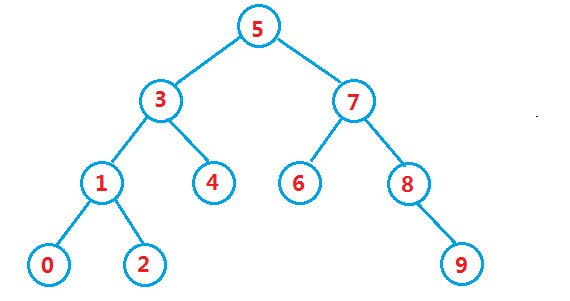
Today we will talk about a special binary tree, binary search tree. Learning binary search tree well will help us understand and master map and set later.
Binary search tree concept
Binary search tree, also known as binary sort tree, is either an empty tree or a binary tree with the following properties:
- If its left subtree is not empty, the value of all nodes on the left subtree is less than that of the root node
- If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of the root node
- Its left and right subtrees are also binary search trees
Binary search tree operation
For most of the operations of binary search tree, we mostly realize them through loop and recursion. However, recursive stack consumption is large. Although the code is relatively simple, I still advocate non recursive writing.
1. Find
Finding is relatively simple. Because of the distinctive characteristics of binary search tree, we just need to constantly compare the nodes to be found with the nodes in the tree:
1. Circulation method
Node* find(const K& key) {
if (_root == nullptr) {
return false;
}
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
cur->_right;
}
else if(cur->_key>key) {
cur->_left;
}
else {
return cur;
}
}
return nullptr;
}
- Recursive method
Node* _findR(Node* root, const K& key) {
if (root == nullptr) {
return nullptr;
}
else {
if (cur->_key < key) {
return _findR(cur->_right, key);
}
else if (cur->_key > key) {
return _findR(cur->_right, key);
}
else {
return cur;
}
}
}
2. Insert
The idea of inserting is divided into two steps: the first is not to find the location to insert, and then create a node to insert.
Circular writing:
//insert
bool insert(const K& key)
{
if (_root == nullptr) {
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
}
else {
return false;
}
}
cur = new Node(key);
if (cur->_key > parent->_key) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
return true;
}
Recursion:
//Recursive version insertion
bool _insertR(Node* &root,const K& key) {
if (root == nullptr) {
root = new Node(key);
return true;
}
Node* cur = root;
else{
if (cur->_key > key) {
return insertR(cur->_left, key);
}
else if(cur->_key<key){
return insertR(cur->_right, key);
}
else {
return false;
}
}
}
3. Delete
Deletion is a difficulty of binary sort tree. We cannot destroy its nature while deleting. We need to analyze different situations in detail:
For nodes to be deleted:
-
No child nodes (leaf nodes)
This is the simplest case. You can delete it directly without affecting other nodes -
There is one node
In this case, we can point the parent node of the point to be deleted to the child node of the node to be deleted, and then talk about deleting the point to be deleted.
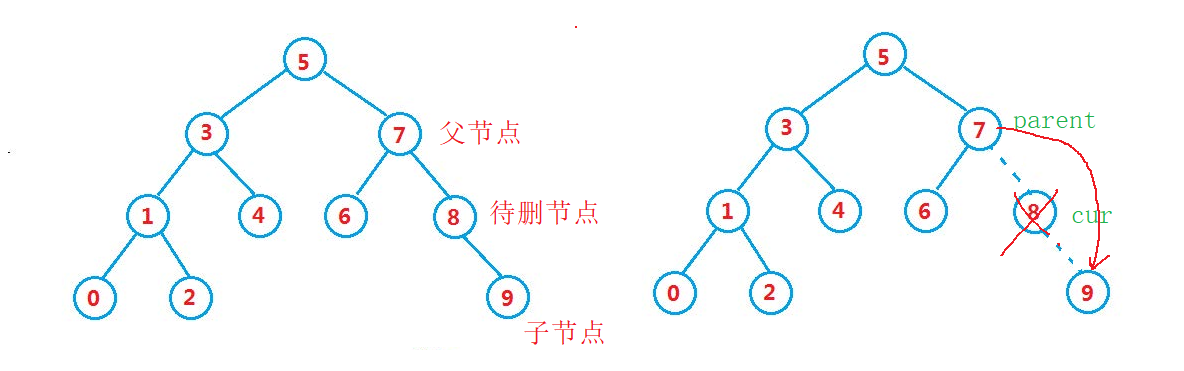
- There are two nodes
For the case with two child nodes, we need to use the "substitution deletion method".
We need to find the minimum value of the right subtree or the maximum value of the left subtree of the deleted node, assign the found value to the node to be deleted, and then delete the minimum value of the right subtree or the maximum value of the left subtree.
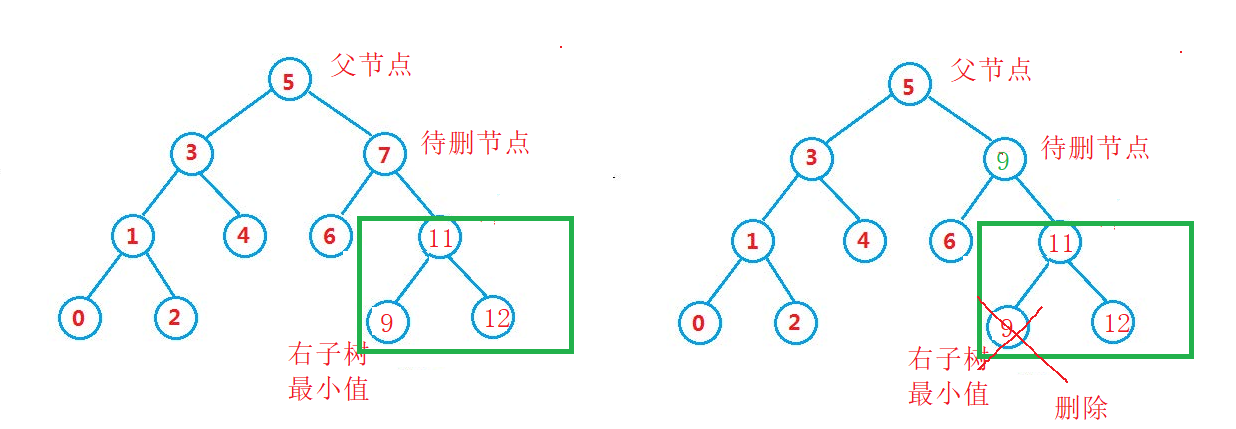
Circular writing:
bool erase(const K& key) {
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
}
else {
if (cur->_left == nullptr) {
if (cur == _root)
{
_root = cur->_right;
}
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr) {
if (cur == _root)
{
_root = cur->_left;
}
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
}
else {
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left) {
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (minRightParent->_left == minRight) {
minRightParent->_left = minRight->_right;
}
else {
minRightParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
Recursion:
bool _eraseR(Node* &root, const K& key) {
if (root == nullptr)
return false;
if (root->_key < key) {
return _eraseR(root->_right, key);
}
else if (root->_key > key) {
return _eraseR(root->_left, key);
}
else {
Node* del = root;
if (root->_left == nullptr) {
root = root->_right;
}
else if (root->_right == nullptr) {
root = root->_left;
}
else {
Node* minRight = root->_right;
while (minRight->_left) {
minRight = minRight->_left;
}
root->_key = minRight->_key;
return _eraseR(root->_right, minRight->_key);
}
delete del;
return true;
}
}
Implementation of binary search tree
For a complete binary search tree. We also add copy construction and assignment, copy and destruction, destructor and so on. I won't repeat them one by one here, but directly post the complete code:
#pragma once
namespace yyk
{
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr),
_right(nullptr),
_key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
//copy construction
BSTree(const BSTree<K>& t)
{
_root = _copyR(t._root);
}
// Assignment copy
BSTree<K>& operator=(BSTree<K> t)
{
std::swap(_root, t._root);
return *this;
}
//Destructor
~BSTree()
{
_Destroy(_root);
}
//insert
bool insert(const K& key)
{
if (_root == nullptr) {
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
}
else {
return false;
}
}
cur = new Node(key);
if (cur->_key > parent->_key) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
return true;
}
//query
Node* find(const K& key) {
if (_root == nullptr) {
return false;
}
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
cur->_right;
}
else if(cur->_key>key) {
cur->_left;
}
else {
return cur;
}
}
return nullptr;
}
//delete
bool erase(const K& key) {
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
}
else {
if (cur->_left == nullptr) {
if (cur == _root)
{
_root = cur->_right;
}
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr) {
if (cur == _root)
{
_root = cur->_left;
}
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
}
else {
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left) {
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (minRightParent->_left == minRight) {
minRightParent->_left = minRight->_right;
}
else {
minRightParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void InOrder() {
_InOrder(_root);
cout << endl;
}
void insertR(const K& key) {
_insertR(_root,key);
}
void findR(const K& key) {
_findR(_root, key);
}
void eraseR(const K& key) {
_eraseR(_root, key);
}
private:
//Middle order traversal
void _InOrder(Node* root) {
if (root == nullptr) {
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
//Recursive version insertion
bool _insertR(Node* &root,const K& key) {
if (root == nullptr) {
root = new Node(key);
return true;
}
Node* cur = root;
else{
if (cur->_key > key) {
return insertR(cur->_left, key);
}
else if(cur->_key<key){
return insertR(cur->_right, key);
}
else {
return false;
}
}
}
//Recursive version lookup
Node* _findR(Node* root, const K& key) {
if (root == nullptr) {
return nullptr;
}
else {
if (cur->_key < key) {
return _findR(cur->_right, key);
}
else if (cur->_key > key) {
return _findR(cur->_right, key);
}
else {
return cur;
}
}
}
//Recursive version deletion
bool _eraseR(Node* &root, const K& key) {
if (root == nullptr)
return false;
if (root->_key < key) {
return _eraseR(root->_right, key);
}
else if (root->_key > key) {
return _eraseR(root->_left, key);
}
else {
Node* del = root;
if (root->_left == nullptr) {
root = root->_right;
}
else if (root->_right == nullptr) {
root = root->_left;
}
else {
Node* minRight = root->_right;
while (minRight->_left) {
minRight = minRight->_left;
}
root->_key = minRight->_key;
return _eraseR(root->_right, minRight->_key);
}
delete del;
return true;
}
}
//Recursive copy function
Node* _copyR(Node* root) {
if (root == nullptr) {
return nullptr;
}
Node* newRoot = new Node(root->_key);
newRoot->_left = _copyR(root->_left);
newRoot->_right = _copyR(_root->_right);
return newRoot;
}
//Recursive version destruction function
void _Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
Node* _root = nullptr;
};
}
Binary search tree application
- K model: in K model, only the key is used as the key, and only the key needs to be stored in the structure. The key is the value to be searched. For example, give a word word and judge whether the word is spelled correctly. The specific methods are as follows:
- Take each word in the word set as the key to build a binary search tree
- Retrieve whether the word exists in the binary search tree. If it exists, it will be spelled correctly, and if it does not exist, it will be misspelled
- KV model: each key has its corresponding Value value, that is, the key Value pair of < key, Value >. This method is very common in real life: for example, an English Chinese dictionary is the corresponding relationship between English and Chinese. The corresponding Chinese can be quickly found through English, and the English word and its corresponding Chinese < word, Chinese > constitute a key Value pair; Another example is to count the number of words. After successful statistics, the number of occurrences of a given word can be quickly found. The word and its number of occurrences are < word, count > to form a key Value pair.
For example, a simple English Chinese Dictionary dict is implemented, and the corresponding Chinese can be found in English. The specific implementation methods are as follows:
- < word, Chinese meaning > constructs a binary search tree for Key value pairs. Note: the binary search tree needs to be compared. When comparing Key value pairs, only Key is compared
- When querying English words, you can quickly find the corresponding key by giving the English words
namespace KEY_VALUE
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
: _left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
V& operator[](const K& key)
{
pair<Node*, bool> ret = Insert(key, V());
return ret.first->_value;
}
pair<Node*, bool> Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return make_pair(_root, true);
}
// Find the location to insert
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(key, value);
if (parent->_key < cur->_key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return make_pair(cur, true);
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// delete
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
// Find the smallest node in the right tree to replace the deletion
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (minRight == minRightParent->_left)
minRightParent->_left = minRight->_right;
else
minRightParent->_right = minRight->_right;
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":"<<root->_value<<endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
}
KEY_ Two applications of value:
- Dictionaries
void TestBSTree2()
{
KEY_VALUE::BSTree<string, string> dict;
dict.Insert("sort", "sort");
dict.Insert("insert", "insert");
dict.Insert("tree", "tree");
dict.Insert("right", "right");
// ...
string str;
while (cin >> str)
{
if (str == "Q")
{
break;
}
else
{
auto ret = dict.Find(str);
if (ret == nullptr)
{
cout << "Spelling error, please check your words" << endl;
}
else
{
cout << ret->_key << "->" << ret->_value << endl;
}
}
}
}
- Count the number of words
void TestBSTree3()
{
// Counts the number of occurrences of a string. It is also a classic key/value
string str[] = { "sort", "sort", "tree", "insert", "sort", "tree", "sort", "test", "sort" };
KEY_VALUE::BSTree<string, int> countTree;
//Method 1:
for (auto& e : str)
{
auto ret = countTree.Find(e);
if (ret == nullptr)
{
countTree.Insert(e, 1);
}
else
{
ret->_value++;
}
}
// Method 2:
/*for (auto& e : str)
{
countTree[e]++;
}*/
countTree.InOrder();
}
Performance analysis of binary search tree
Insert and delete operations must be searched first. The search efficiency represents the performance of each operation in the binary search tree.
For a binary search tree with n nodes, if the search probability of each element is equal, the average search length of the binary search tree is a function of the depth of the node in the binary search tree, that is, the deeper the node, the more comparisons.
However, for the same key set, if the insertion order of each key is different, binary search trees with different structures may be obtained:
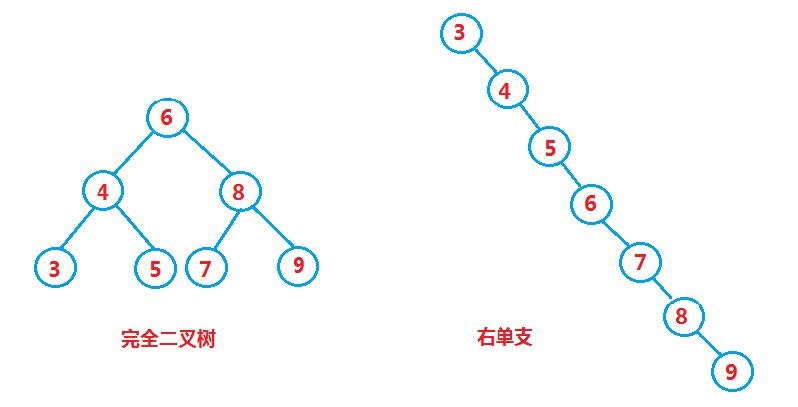
The average number of binary tree search is log2
In the worst case, the binary search tree degenerates into a single branch tree, and its average comparison times is N/2
Problem: if it degenerates into a single tree, the performance of binary search tree will be lost. Can we improve it? No matter what order the key is inserted, it can be the best performance of binary search tree? The answer is there, but we'll talk about it later.