c + + various classical sorting algorithms
Starting today, write down what you have learned about looking for a job.
1, Various sortalgorithm Time and space complexity and stability of ⭐⭐⭐⭐⭐
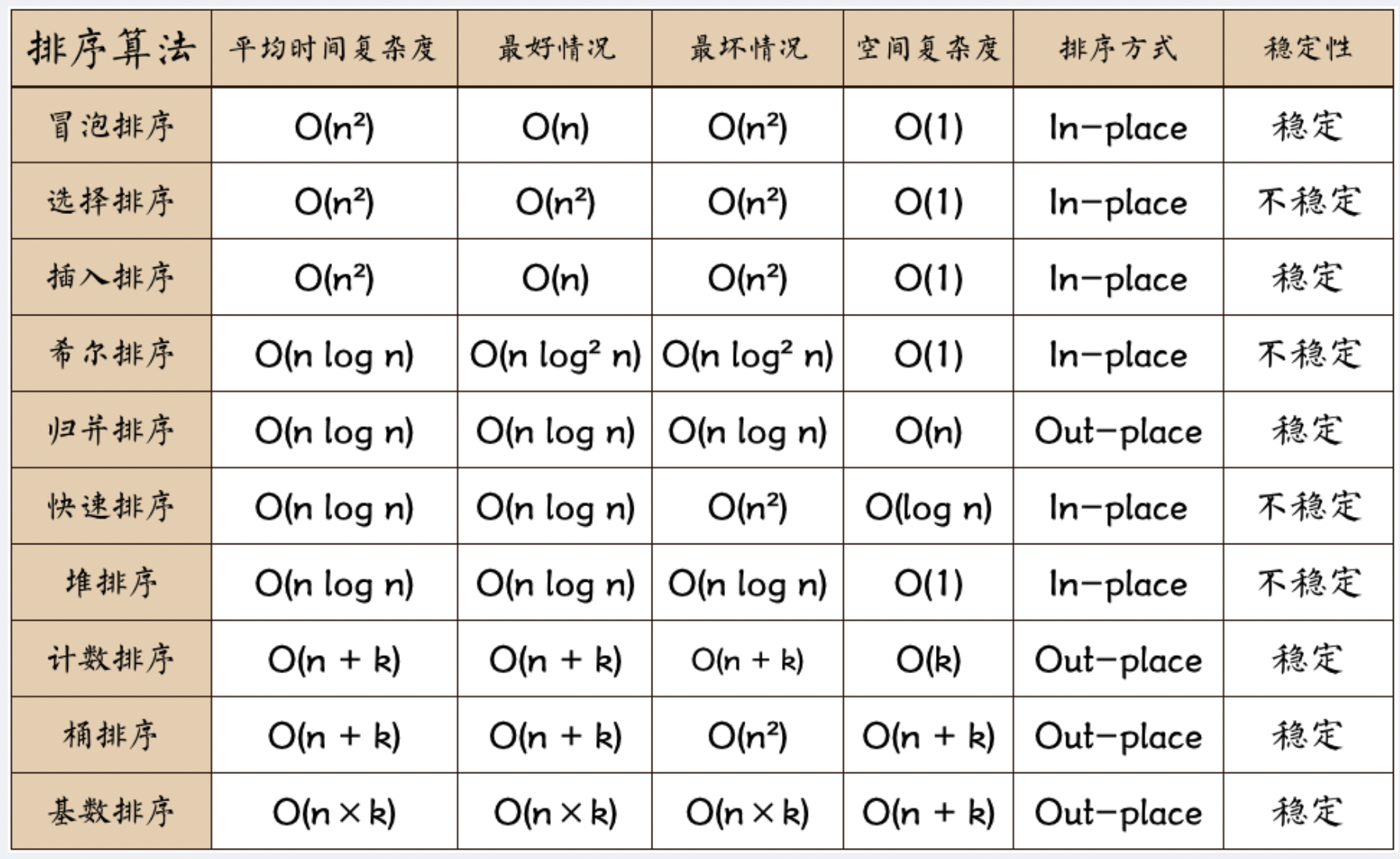
2, (various) sortalgorithm When is the best and worst case (especially fast platoon)
3, Bubbling sort⭐⭐⭐⭐
// Bubble sort the two adjacent elements are compared with each other until the end, and then start again.
void BubbleSort(int a[], int len) {
int tmp;
int exchange = 1;
for (int i = 0; (i < len - 1) && (exchange > 0); i++) {
exchange = 0;
for (int j = 0; j < len - 1 - i; j++) {
if (a[j] > a[j + 1]) {
tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
exchange = 1;
}
}
}
}
The best time: time complexity O(n). The elements are arranged in order
Worst time: time complexity O( n 2 n^2 n2) . Data elements are in reverse order
General: time complexity O( n 2 n^2 n2).
Stability: during each comparison, if two adjacent elements want to wait, the order is not exchanged.
Space complexity: O(1)
4, Insert sort⭐⭐⭐⭐
//Insert sort
//Take out a number and compare it with the previous number. If you encounter a number no larger than it, insert it
void InsertSort(int a[],int len) {
int tmp;
for (int i = 0; i < len; i++) {
tmp = a[i];
int k = i; // Record the insertion position
for (int j = i-1; (j >= 0) && (a[j] > tmp); j--) {
a[j + 1] = a[j];
k = j;
}
a[k] = tmp;
}
}
Best case: time complexity O(n) the whole sequence has been sorted. The first element is compared 0 times, the second element is compared 1 time, and the nth element is compared 1 time.
Worst case: time complexity O( n 2 n^2 n2) reverse order of the whole sequence
Average time complexity: o( n 2 n^2 n2)
Stability: stable
Space complexity: O(1)
5, Hill sort⭐⭐⭐⭐
- Firstly, the large data set is divided into several small data sets, and then each small data set is inserted and sorted.
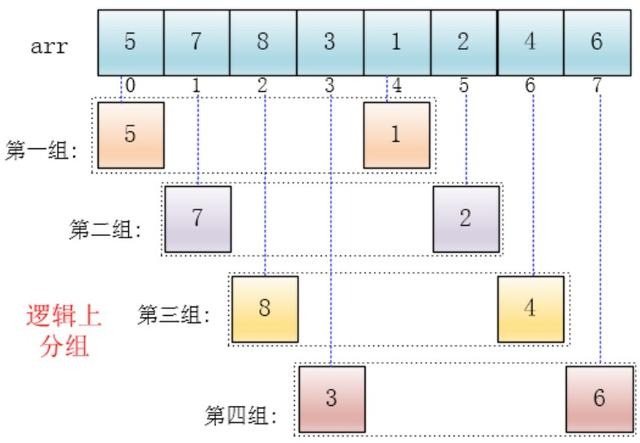
The initial increment gap=length/2. This example is a group with a subscript distance of 4 points, that is, those with a subscript difference of 4 are divided into a group. For example, in this example, a[0] and a[4] are a group, a[1] and a[5] are a group
After insertion sorting is completed
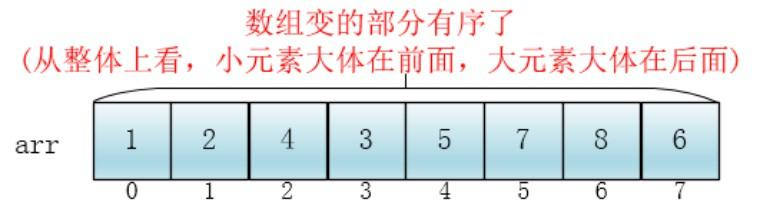
-
Reduce the increment to half of the previous increment: gap =4/2. Continue to divide the groups. At this time, there are more elements in each group. However, the array becomes partially ordered, and the insertion sorting efficiency is also higher.
-
Set the increment to half of the previous increment: gap=2/2 `, then the whole array is divided into a group. At this time, the whole array is close to order, and the insertion sorting efficiency is high.
//Shell Sort //Solve the problem that the maximum value needs to move n-1 positions in the first place void ShellSort(int a[], int n) { int gap = n; int tmp; while (gap > 1) { gap = gap / 3 + 1; for (int i = gap; i < n; i += gap) { int k = i; tmp = a[i]; for (int j = i -gap; (j >= 0) && (a[j] > tmp); j -= gap) { a[j + 1] = a[j]; k = j; } a[k] = tmp; } } }- Best case: T(n) = O(nlog2 n) ordered
- Worst case: T(n) = O(nlog_2 n)
- Average: T(n) =O(nlog2n)
- Stability: unstable. Although the insertion sort is stable, Hill sort may jump during insertion, so it is not stable and may destroy the stability
6, Merge sort⭐⭐⭐⭐
That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one ordered table.
The input sequence with length n is divided into two subsequences with length n/2; The two subsequences are sorted by merging; Merge two sorted subsequences into a final sorting sequence.
//Merge sort
//That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one ordered table.
//The input sequence with length n is divided into two subsequences with length n/2; The two subsequences are sorted by merging; Merge two sorted subsequences into a final sorting sequence.
//Firstly, it is assumed that the two arrays are ordered. They are combined according to the ordered sequence to form an ordered sequence
void merge(int a[],int low ,int mid,int high, int tmp[]) {
int i = low; //Start position of left subarray
int j = mid + 1; //Start position of right subarray
int t = 0; //Temporary space pointer
//First determine the size of the starting position of the array to be merged, and then copy the array to tmp array storage.
// Compare each element of the 2 arrays and sort in size order.
while (i <= mid && j <= high) {
if (a[i] < a[j]) {
tmp[t++] = a[i++];
}
else
tmp[t++] = a[j++];
}
//reference resources https://www.bilibili.com/video/BV1Pt4y197VZ?from=search&seid=6438701192248743313
//If there is only one element in the right half, after the above position is placed, the elements in the left half can be placed directly
//Fill the remaining elements on the left into temp
while (i <= mid) {
tmp[t++] = a[i++];
}
//Fill the rest of the right sub array into temp
while (j <= high) {
tmp[t++] = a[j++];
}
//Copy the fused data to the subspace corresponding to the original data
t = 0;
while (low <= high) {
a[low++] = tmp[t++];
}
}
void Msort(int a[], int low, int high, int tmp[]) {
if (low < high) {
int mid = (low + high) / 2;
//Recursive partition of left half region
Msort(a,low,mid,tmp);
//Recursive partition of the right half
Msort(a,mid + 1,high,tmp);
//Merge left and right halves
merge(a,low,mid,high,tmp);
}
}
**Time complexity: * * O(NlogN)
**Best time complexity: * * O(NlogN)
Space complexity: O(N)
**Features: * * the time complexity is independent of whether the data is orderly or not. Is a stable sorting algorithm. It is the only stable sorting algorithm among the advanced sorting algorithms.
**Application: * * if sorting is required to be stable and space is not important, merge algorithm shall be used
7, Select sort ⭐⭐⭐⭐
//Select sort
//The time complexity is O (n2), the smaller the scale, the better, and does not occupy additional space
//Find the smallest in the unordered and put it in the starting position, and then find the smallest and put it in the second position
void SelectSort(int a[], int len) {
for (int i = 0; i < len; i++) {
int minindex = i;
for (int j = i + 1; j < len; j++) {
if (a[minindex] > a[j]) {
minindex = j;
}
}
swap(a[i],a[minindex]);
}
}
Best time: time complexity O( n 2 n^2 n2)
Worst time: time complexity O( n 2 n^2 n2)
General: time complexity O( n 2 n^2 n2)
Stability: unstable
Space complexity: O(n)
8, Fast sort⭐⭐⭐⭐⭐
//Quick sort
//Select a number as the benchmark, so that the left of the array is less than the benchmark and the right is greater than the benchmark
//recursive partitioning
//Partition function
int partion(int a[], int low, int high) {
//Select the first element as the standard
int index = a[low];
//Push the left and right pointers to the middle,
while (low < high) {
//If the number on the right is larger than the standard, do not move, otherwise switch to the left
while ((low < high) && a[high] >= index) {
high--;
}
while ((low < high) && a[low] <= index) {
low++;
}
swap(a[low],a[high]);
}
}
void Qsort(int a[], int low,int high) {
if (low < high) {
int index = partion(a,low,high);
//recursive partitioning
Qsort(a,low,index - 1);
Qsort(a,index,high);
}
}
**Time complexity: * * o( n l o g n nlogn nlogn)
**Best time complexity: o( n l o g n nlogn nlogn) -- correspondence - (additional) space complexity: * * o( o g n ogn ogn)
**Worst time complexity: o( n 2 n^2 n2) -- correspondence -- (additional) space complexity: * * O(n) -- in the worst case, fast exhaust degenerates into bubbling
**Average time complexity: * * o( n l o g n nlogn nlogn)
**Features: * * is an unstable algorithm.
#9, It is required to master the partition function of fast scheduling and the Merge function of merging ⭐⭐⭐
#Reference:
https://blog.csdn.net/zhangsy_csdn/article/details/91483600
https://www.bilibili.com/video/BV1bz411e7vY
)-- in the worst case, the fast discharge degenerates into bubbling
**Average time complexity: * * o( n l o g n nlogn nlogn)
**Features: * * is an unstable algorithm.
9, It is required to master the partition function of fast scheduling and the Merge function of merging ⭐⭐⭐
reference resources:
https://blog.csdn.net/zhangsy_csdn/article/details/91483600
https://www.bilibili.com/video/BV1bz411e7vY