Today, let's talk about monotonic queues and stacks.
Although these two data structures are not directly implemented in c + + stl, it is easy to use monotonic queue (stack) in the process of doing questions, especially in some difficult questions.
Monotone queue
1.1 introduction to monotone queue
Monotonic queue is the monotonous relationship between the elements in the queue. Moreover, both the head and tail of the queue can be out of the queue, and only the tail of the queue can be in the queue. In essence, it is realized by double ended queue deque.
Let's take a monotonically decreasing queue as an example:
Let's make an analogy first: when you are cooking in the canteen, there is a person who is tall and big and runs in a hurry to see such a long queue. He is impatient. Starting from the last person in the queue, he drives away those who are easy to bully, stands by himself, and stops until he can't do it. This is a monotonous decreasing queue. That is, queues that allow both ends to pop up and only one end to insert (queues that allow both ends to insert and only one end to pop up also belong to double ended queues).
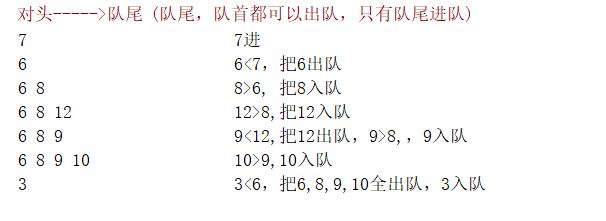
We take 7 6 8 12 9 10 3 as an example to establish a monotonically decreasing queue:

Similarly, if a monotonically increasing queue is established:
We can also use another example: when queuing, the younger child should take priority. If the child finds that the person in front is older than him, he will be driven out of the queue until the person in front is younger than him, and he won't move.
Obviously, the opponent of the last monotone queue is either the largest element or the smallest element. Obviously, if you just want to find the best value in the sequence, there is no need to use a queue to "in and out" the elements, and everyone is dizzy.
In my humble opinion, monotone queues are generally used to find extreme values in a dynamic cell.
Next, let's feel it directly through examples.
1.2 application of monotone queue
1.2.1 maximum value of sliding window
1.2.1.1 Title Description
Title: give you an integer array nums, with a sliding window of size k moving from the leftmost side of the array to the rightmost side of the array. You can only see k numbers in the sliding window. The sliding window moves only one bit to the right at a time. Returns the maximum value in the sliding window
Case 1:
Input: nums = [1,3,-1,-3,5,3,6,7], k = 3 Output:[3,3,5,5,6,7] Explanation: Position of sliding window Maximum --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
Case 2:
Input: nums = [1], k = 1 Output:[1]
1.2.1.2 conclusion idea
In fact, there are three ways to solve this problem. Let's not talk about the monotonous queue first, but now talk about the method of large priority queue.
The reason is that [monotone queue method] is actually an optimization of [priority queue method]. It is difficult to directly talk about monotone queue, which is difficult to understand.
ps: Here we directly skip the high complexity (O(nk)) method of traversing each small window.
Method 1 (priority queue)
For "maximum", we can think of a very suitable data structure, that is, priority queue (heap), in which the large root heap can help us maintain the maximum value in a series of elements in real time.
In c + +, the adapter implemented by heap is priority_queue (priority queue). Students who don't know can read the following blog:
[C + +] teach you to write your own Stack and Queue classes
Let's take the array [1,9, - 1, - 3,5,3,6,7] (k=3) as an example to explain. I'll put the step diagram below first:

- Initially, we put the first kk elements of the array \ textit{nums}nums into the priority queue [step 1 in the above figure].
- Whenever we move the window to the right, we can put a new element into the priority queue [steps 2, 3, 4, 5 and 6 in the above figure]. At this time, the element at the top of the heap is the maximum value of all elements in the heap. However, the maximum value in this heap may not be what we want. For example [step 3 in the figure above], we will join the team with 9. At this time, 9 is the maximum value, but obviously 9 is not in the range, which is obviously not the maximum value of the current range. In this case, the position of this value in the array must appear on the left side of the left boundary of the sliding window. (that is, 9 is on the left of - 1). Therefore, when we continue to move the window to the right, this value will only slide the window farther and farther, and we can permanently remove it from the priority queue.
- We continue to remove the top of the heap element until it does appear in the sliding window. At this point, the heap top element is the maximum value in the sliding window. In order to easily judge the position relationship between the top element and the sliding window, we need to store the element itself and its subscript in the priority queue at the same time.
The reason why it is said here is "continuously remove the elements at the top of the heap until they actually appear in the sliding window". This is because sometimes there may be situations where several elements in the queue are not actually in the sliding window:
For example, [1,9,9, - 3,5,3,6,7], in step 4 of the figure below, we delete the team head element twice to end.

Implementation code
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
priority_queue<pair<int, int>> q;
for (int i = 0; i < k; ++i) {
q.emplace(nums[i], i);
}
vector<int> ans = {q.top().first};
for (int i = k; i < n; ++i) {
q.emplace(nums[i], i);
while (q.top().second <= i - k) {
q.pop();
}
ans.push_back(q.top().first);
}
return ans;
}
};
Complexity analysis:
-
Time complexity: O(nlogn), where nn is the length of array nums. In the worst case, the elements in the array num are monotonically increasing, so all the elements are included in the final priority queue, and no elements are removed. Since the time complexity of putting an element into the priority queue is O(logn), the total time complexity is O(nlogn).
-
Space complexity: O(n), that is, the space required by the priority queue. All spatial complexity analysis here does not consider the O(n) space required by the returned answer, and only calculates the use of additional space.
Method 2 (monotone queue)
We can continue to optimize along the idea of method 1.
As we know, the key of priority queue is to arrange the elements in a window in descending order, but in fact, the queue does not need to maintain all the elements in the window. You only need to maintain the element that may become the maximum value in the window, while maintaining its monotonicity and decrement.
What's the meaning of this? For example, in a moving window, two numbers satisfy nums[i] < nums [j], and I < j. Then when the sliding window moves to the right, as long as I is still in the window, j must also be in the window, which is guaranteed by I on the left side of j. At the same time, since num[i] < num [j], num[i] cannot become the maximum. Then leaving num[i] in the queue before loses value.
We use a window [2 3 5 1 4] to compare the two methods.

For example, a country has several crown princes, but some of them have no chance at all, so they simply quit the competition. The court doesn't have to waste resources to train them.
After understanding the general optimization idea, let's take a look at the process:
As usual, look at the picture. Let's take the array [2 3 5 1 4 8 9 0] (k=5) as an example:

- When the sliding window moves to the right, we need to put a new element in the queue. In order to maintain the nature of the queue, we will constantly compare the new elements with the elements at the end of the queue. If the former is greater than or equal to the latter, the elements at the end of the queue can be permanently removed and we pop them out of the queue. We need to keep doing this until the queue is empty or the new element is smaller than the element at the end of the queue.
- Since the element corresponding to the subscript in the queue is strictly monotonically decreasing, the element corresponding to the subscript at the head of the queue is the maximum value in the sliding window. However, as in method 1, the maximum value may be on the left side of the left boundary of the sliding window, and it will never appear in the sliding window as the window moves to the right. Therefore, we also need to constantly pop up elements from the team head until the team head element is in the window. (not shown in the figure)
In order to realize the monotonous queue, deque can be used to pop up the queue at the same time.
code implementation
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
deque<int> q;
//Use the first window to initialize the monotone queue
for (int i = 0; i < k; ++i) {
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
q.push_back(i);//The queue stores subscripts
}
//ans stores the maximum value of each window
vector<int> ans = {nums[q.front()]};
for (int i = k; i < n; ++i) {
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
//Check whether the maximum element is in the window interval
if (q.front() <= i - k) {
q.pop_front();
}
ans.push_back(nums[q.front()]);
}
return ans;
}
};
Complexity analysis:
-
Time complexity: O(n), where n is the length of the array \ num. Each subscript is put into the queue exactly once and ejected from the queue at most once, so the time complexity is O(n)O(n).
-
Spatial complexity: O(k). Different from method 1, the data structure we use in method 2 is bidirectional, so "constantly ejecting elements from the head of the queue" ensures that there will be no more than k+1 elements in the queue, so the space used by the queue is O(k)
1.3 simulation of monotone queue
After reading the above questions, in fact, we can also implement a MyQueue class ourselves, which is equivalent to a container adapter.
When designing monotone queues, push() and pop() should keep the following rules:
- push(value): if the element value of the push is greater than the value at the end of the queue, pop the element at the end of the queue until value is less than or equal to the value of the entry element, or until the queue is empty.
- pop(): if the value of the element to be removed from the window is equal to the queue header element of the monotonic queue, the queue pops up the queue header element, otherwise no operation will be done. Although this expression is a little different from the title above, it means the same.
The code of myQueue is posted below:
#pragma once
namespace yyk {
template<class T,class Compare=greater<T>>
class myQueue {
public:
void push(T value) {
Compare com;
while (!que.empty() && com(value , que.back())) {
que.pop_back();
}
que.push_back(value);
}
void pop(T value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
const T& front() {
return que.front();
}
bool empty() {
return que.empty();
}
private:
deque<T> que;
};
}
At the same time, we can also use the monotone stack we simulated to realize [maximum sliding window]
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#include"MyQueue.h"
void Print(yyk::myQueue<int> que) {
while (!que.empty()) {
cout << que.front() << " ";
que.pop(que.front());
}
cout << endl;
}
vector<int>maxSlidingWindow(vector<int>& nums, int k) {
yyk::myQueue<int> que;
vector<int>ans;
for (int i = 0; i < k; i++) {
que.push(nums[i]);
}
ans.push_back(que.front());
Print(que);
for (int i = k; i < nums.size(); ++i) {
que.pop(nums[i - k]);
que.push(nums[i]);
ans.push_back(que.front());
Print(que);
}
return ans;
}
int main() {
vector<int>v = { 1,9,9,-3,5,3,6,7 };
maxSlidingWindow(v, 3);
}
If the problem requires us to find the minimum value at this time, we just need to add the second template parameter when instantiating myQueue.
yyk::myQueue<int,Less<int>> que;
1.4 other examples
Then add.