Hello, everyone! This article is a follow-up to the previous article. Different from the previous one, this time, the Bayesian classifier is used for number recognition. Bayesian has been taught in probability theory and mathematical statistics. Let's briefly understand it below:

        First, the Bayesian formula is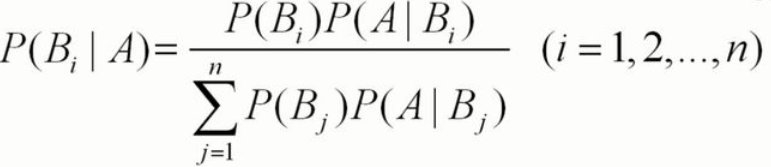

Let's not talk about the specific explanation. Let's talk about where Bayesian is used in number recognition. In addition to the recognition part, the others, including traversing folders and image digitization, remain unchanged; There are ten numbers from 0 to 9, so there are ten terms in the denominator, P(Bj)(j is the subscript) corresponding to 0 to 9, then the probability of each is 1 / 10, and P(Bi) on the molecule is one of 0 to 9, so the probability is also 1 / 10. (if you can't understand it, i suggest you look at Bayes) so we can put forward the denominator and reduce the score, and then the formula Pi/(P1+P2+P3+P4+P5+P6+P7+P8+P9)(Pi is P(A|Bi), and the other values are i respectively). After this happens, i takes a number from 0 to 9, which is the probability that the test sample is this number. For example, i=0, which means that the probability that the test case is 0 is P1/(P1+P2+P3+P4+P5+P6+P7+P8+P9+P10) (1 is the corresponding number 0).

        So how do we find Pin? We count the probability that each bit of the sample is 1, which may be unclear. That is, if the data string of a 0 picture is 0000000000 100000011000010001010000111000000000 (49 bits), we count the number of each bit of 1 bit by bit (as shown in the figure below, i.e. the number of samples with a certain digit of 1 in each sample is counted longitudinally). Finally, divided by the total number, there are 100 samples of a digit in my training library. If we count 46 samples with a first digit of 1 in all samples with a digit of 0, the probability that the first digit of 0 is 1 is 0.46, and the other digits are counted in turn. Other figures are the same as above.

        Finally, we can count the probability that each digit of each number is 1 to form a 10 * 49 two-dimensional array, that is, 10 numbers and 49 digits of each number. Then we take a test case and calculate the probability with 10 numbers in turn. Finally, the obtained probability is compared. So how do we calculate the probability that the test case is a number? Let's simply put 49 digits below As three bits, if the probability of the first, second and third digits of the number 0 being 1 is 0.56, 0.05 and 0.41, and the data string of the test case is 101, then we take the probability of 1 and multiply it directly. If it is 0, subtract this probability from 1 and multiply it, that is, 0.56 * 0.95 * 0.41. Here we almost have all our ideas. (for other ideas, please refer to the last article and put the link below) c + + handwritten numeral recognition based on template matching (super detailed) _m0_57587079 blog CSDN blog

The following is my code. First, opencv has to be installed by itself. Here I give a link. You can refer to the steps of the blogger above

OpenCV installation tutorial under windows (little white tutorial) _HikD_bn blog - CSDN blog

In addition, my Bayes function is too long and should be divided into several functions, which will be better debugged and read

The detailed code explanations are in the comments. Just look carefully and understand. If there are better methods and ideas, welcome to exchange and learn!

#include<iostream>
#include<fstream>
#include<opencv2/opencv.hpp>
#include<opencv2/highgui.hpp>
#include<opencv2/core.hpp>
#Include < io. H > / / API and struct
#include<string.h>
#include<string>
#Include < ssstream > / / string to int data type contains

using namespace std;
using namespace cv;

void ergodicTest(string filename, string name);    //Ergodic function
string Image_Compression(string imgpath);          //Compress the picture and return a string
void Bayes();                                     //Bayesian classifier
int turn(char a);


void main()
{
	const char* filepath = "E:\\learn\\vsfile\\c++project\\pictureData\\train-images";
	ergodicTest(filepath, "train_num.txt");         //Processing training sets
	const char* test_path = "E:\\learn\\vsfile\\c++project\\pictureData\\test-images";
	ergodicTest(test_path, "test_num.txt");
	Bayes();

}

void ergodicTest(string filename, string name)       //Traverse and save the path to files
{
	string firstfilename = filename + "\\*.bmp";
	struct _finddata_t fileinfo;
	intptr_t handle;            //You can't use long, because the precision problem will lead to access conflict. longlong can also be used
	string rout = "E:\\learn\\vsfile\\c++project\\pictureData\\" + name;
	ofstream file;
	file.open(rout, ios::out);
	handle = _findfirst(firstfilename.c_str(), &fileinfo);
	if (_findfirst(firstfilename.c_str(), &fileinfo) != -1)
	{
		do
		{
			file << fileinfo.name<<":"<< Image_Compression(filename + "\\" + fileinfo.name) << endl;
		} while (!_findnext(handle, &fileinfo));
		file.close();
		_findclose(handle);
	}
}

string Image_Compression(string imgpath)   //Enter the picture address and return the binary pixel character of the picture
{
	Mat Image = imread(imgpath);               //Input picture
	cvtColor(Image, Image, COLOR_BGR2GRAY);
	int Matrix[28][28];                        //Convert digitization to string type
	for (int row = 0; row < Image.rows; row++)  //Pass the pixels of the picture to the array
		for (int col = 0; col < Image.cols; col++)
		{
			Matrix[row][col] = Image.at<uchar>(row, col);
		}
	string img_str = "";                   //Used to store the result string
	int x = 0, y = 0;
	for (int k = 1; k < 50; k++)
	{
		int total = 0;
		for (int q = 0; q < 4; q++)
			for (int p = 0; p < 4; p++)
				if (Matrix[x + q][y + p] > 127) total += 1;
		y = (y + 4) % 28;
		if (total >= 6) img_str += '1';    //Convert 28 * 28 pictures into 7 * 7, that is, compression
		else img_str += '0';
		if (k % 7 == 0)
		{
			x += 4;
			y = 0;
		}
	}
	return img_str;
}

int turn(char a)  //This function converts a string type to an int type
{
	stringstream str;
	int f = 1;
	str << a;
	str >> f;
	str.clear();
	return f;
}

void Bayes()
{
	ifstream data_test, data_train;     //A file stream that fetches data from two data string files
	string temp;                        //Variable of intermediate temporary string
	double count[10] = { 0 };                      //It is used to count 1 number of each digital sample
	double probability[10][49] = { 0 };
	int t = 0;            //Avoid arithmetic overflow

	for (int i = 0; i < 49; i++)    //Process training samples by column (each sample has 49 bits of data length)
	{
		data_train.open("E:\\learn\\vsfile\\c++project\\pictureData\\train_num.txt");
		for (int j = 0; j < 1000; j++)   //Take data a thousand times in sequence
		{
			getline(data_train, temp);    //Take each row of data in sequence			
			if (temp.length() == 57)   //The original length was 49. Because I have a file name, I want to skip the file name
			{
				t = i + 8;     //t is used instead of i+8 because there is no + - overload in [] of string, as it seems
				if (turn(temp[t]) == 1) count[turn(temp[0])]++;         //The corresponding number is 1 count plus 1
				else continue;
			}
			else if(temp.length() == 58)
			{
				t = i + 9;   //Some file names are 8 bits, others are 9 bits
				if (turn(temp[t]) == 1) count[turn(temp[0])]++;         //Corresponding number
				else continue;
			}
		}
		data_train.close();  //Be sure to pay attention to the timing of file stream opening and closing. There is a complete traversal (getline) between opening and closing
		for (int q = 0; q < 10; q++)
		{
			probability[q][i] =count[q] / 100.0;                //Calculate the probability of each bit 1 of each digital data sample
			count[q] = 0;//The loop also uses count, so it needs to be initialized
		}
	}

	double probab[10] = { 1,1,1,1,1,1,1,1,1,1 };     //The array is the probability of this number (10 numbers)
	data_test.open("E:\\learn\\vsfile\\c++project\\pictureData\\test_num.txt");
	double temp_prob = 0;             //Intermediate variable of comparative possibility: probability
	int temp_num = -1;                //Intermediate variable of comparative possibility: number
	bool flag = true;                 //If the sign refuses to identify, false will refuse
	int num_r = 0, num_f = 0, num_t = 0;   //Respectively means reject, error and correct
	for (int d = 0; d < 200; d++)    //200 test samples
	{
		for (int o = 0; o < 10; o++) probab[o] = 1;//Initialize the probability array. Although there is initialization in the front, our loop will be used multiple times, so we need to initialize once every loop
		getline(data_test, temp);
		for (int y = 0; y < 10; y++)   //And each number to get a probability, that is, the test case is the probability of this number
		{
			for (int s = 0; s < 49; s++)  //49 bits correspond to the probability obtained by de accumulation multiplication
			{
				if (temp.length() == 57)
				{
					t = s + 8;
					if (turn(temp[t]) == 1) probab[y] *=1+probability[y][s];        //Plus 1 is because the multiplication of the zeros is smaller, which is difficult to compare, and some probabilities may be 0,
					else probab[y] *= 2 - probability[y][s]; //Similarly, the probability of 0 should be added with 1
				}
				else
				{
					t = s + 9;
					if (turn(temp[t]) == 1) probab[y] *=1+probability[y][s];         //Corresponding number
					else probab[y] *= (2 - probability[y][s]);
				}
			}
		}

		flag = true;         //Flag set true
		temp_prob = 0;       //Reset intermediate variable
		temp_num = -1;       //Do not identify as any value before starting
		for (int l = 0; l < 10; l++)  //Compare the probability that the test case is a number to determine the largest one
		{
			if (probab[l] > temp_prob)
			{
				temp_prob = probab[l];
				temp_num = l;
				flag = true;          //Not rejected
			}
			else if (probab[l] == temp_prob )
			{
				flag = false;          //Reject identification
			}
		}
		if (!flag)
		{
			num_r++;
		}
		else
		{
			cout << temp[0] << " " << temp_num << endl;
			if (temp_num == turn(temp[0]))
			{
				cout << "Identified as:" << temp_num << endl;
				num_t++;
			}
			else
			{
				cout << "Recognition error!" << endl;
				num_f++;
			}
		}
	}
	data_test.close();
	cout << "The rejection rate is:" << num_r / 200.0 << endl;
	cout << "The correct recognition rate is:" << num_t / 200.0 << endl;
	cout << "The error recognition rate is:" << num_f / 200.0 << endl;
}

  Note that the sample images used in my code are processed binary bmp images. In addition, the txt document in the code needs to be created manually. Partners can modify it and add statements to create text.

Once a day: study hard and make progress every day!