4.1 Boolean Logic
Boolean comparison operator
== != < > <= >=
Boolean Operator for Boolean Value Processing
! &|^ (XOR)
Conditional Boolean Operator
&&|| Better performance than & and | e.g. & & just judge the previous Boolean value to be false and the overall value to be false without calculating the latter Boolean value.
Boolean assignment operator
&= |= ^=
2. Bit Operator
& | ^ ~
Displacement operator * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Displacement assignment operator=<<=
3. Operator priority (update)
++ (used as a prefix); (), +, -(unitary),!,~
*,/,%
+,-
<<,>>
<,>,<=,>=
==,!=
&
^
|
&&
||
= *=,/=,%=,+=,-=,>==,<=,&=,^=,|= assignment operator
++ (used as a suffix)
4.2 goto statement
goto <labelName>
4.3 Branch
1. Ternary Operator
? :
2.if statement
if(){}else{}
3.switch statement
switch()
{
case val1:......;break;
case val2:......;break;
......
Default: If no val ue matches, default, execute the code in default
}
Declare constants: Specify variable types and keyword consts, and assign values to them.
4.4. Loop: Repeated Execution Statement
1.do loop
do
{Execute once to determine the value in while(), true to execute again, false to exit the loop
}while();
2.while loop
When () {} first judges the value in while(), true begins to execute
3.for loop
for(int i=0;i<4,i++){}
4. Cycle interruption
break: End the loop immediately
continue: Terminate the current loop immediately and enter the next one
goto: Jump out of the loop to the designated tag location
return: Jump out of the loop and the function that contains the loop
5. Infinite cycle
while(true) {} Exit using break, etc.
Mandelbrot collection example (the sample code given in this book uses C#)
class Program { //Mandelbrot Every position in an image corresponds to a formula. N=x+y*i A complex number. In fact, the number part is x,The imaginary part is y,i yes-1 The square root. Located in the image x and y Coordinates correspond to imaginary numbers x and y Part //Parameters for each position in an image N To express, it is x*x+y*y The square root. If this value is greater than or equal to 2, the corresponding position value of this number is 0. If the parameter N If the value is less than 2, the N Change the value to N*N-N(N=(x* x-y* y-x)+(2*x* y-y)*i)),And test the new one again. N Value. If this value is greater than or equal to 2, the corresponding position value of this number is 1. This process continues until we assign a value to the position in the image or iterate more than the specified number of times. static void Main(string[] args) { //N Real and imaginary parts double realCoord, imagCoord; //Storing temporary information in computing double realTemp, imagTemp, realTemp2, arg; //Recorded in parameters N(arg)Number of iterations equal to or greater than 2 int iterations; //Select the appropriate boundary value to display Mandelbrot The main part of the image, if you want to enlarge the image, you can enlarge these boundary values. for (imagCoord = 1.2; imagCoord >= -1.2; imagCoord -= 0.05) { //Two for Cyclic processing of a point in an image. N Specify a value. for (realCoord = -0.6; realCoord <= 1.77; realCoord += 0.03) { //initialize variable iterations = 0; realTemp = realCoord; imagTemp = imagCoord; arg = (realCoord * realCoord) + (imagCoord * imagCoord); //2 It's the square root of 4, so it's only calculated. x^2+y^2 Value,while Loop execution iteration, while ((arg < 4) && (iterations < 40)) { //N*N-N Real part realTemp2 = (realTemp * realTemp) - (imagTemp * imagTemp) - realCoord; //N*N-N The imaginary part of imagTemp = (2 * realTemp * imagTemp) - imagCoord; realTemp = realTemp2; arg = (realTemp * realTemp) + (imagTemp * imagTemp); //The value of the current point is stored in iterations in iterations += 1; } //Select the character to be output switch (iterations % 4) { case 0: Console.Write("."); break; case 1: Console.Write("o"); break; case 2: Console.Write("O"); break; case 3: Console.Write("@"); break; } } //The inner loop ends with a line, so the newline character is output. Console.Write("\n"); } Console.ReadKey(); } }
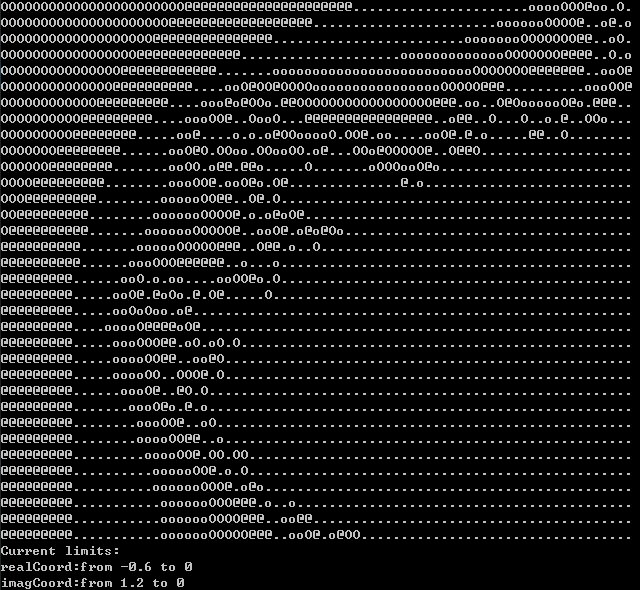
The results of the demonstration are as follows:

Chapter exercises require the user to enter the boundary of the image and display the selected image part. The character output from the current code should be placed on exactly one line of the console application, considering how to occupy each selected image.
The same size of space to maximize the visual area.
class Program { //Mandelbrot Every position in an image corresponds to a formula. N=x+y*i A complex number. In fact, the number part is x,The imaginary part is y,i yes-1 The square root. Located in the image x and y Coordinates correspond to imaginary numbers x and y Part //Parameters for each position in an image N To express, it is x*x+y*y The square root. If this value is greater than or equal to 2, the corresponding position value of this number is 0. If the parameter N If the value is less than 2, the N Change the value to N*N-N(N=(x* x-y* y-x)+(2*x* y-y)*i)),And test the new one again. N Value. If this value is greater than or equal to 2, the corresponding position value of this number is 1. This process continues until we assign a value to the position in the image or iterate more than the specified number of times. static void Main(string[] args) { //N Real and imaginary parts double realCoord, imagCoord; double realMax = 1.77; double realMin = -0.6; double imagMax = -1.2; double imagMin = 1.2; double realStep; double imagStep; //Storing temporary information in computing double realTemp, imagTemp, realTemp2, arg; //Recorded in parameters N(arg)Number of iterations equal to or greater than 2 int iterations; //Select the appropriate boundary value to display Mandelbrot The main part of the image, if you want to enlarge the image, you can enlarge (actually reduce) these boundary values. while (true) { //Set the span to ensure that each selected image occupies exactly the same size of space to maximize the visual area. realStep = (realMax - realMin) / 79; imagStep = (imagMax - imagMin) / 48; for (imagCoord = imagMin; imagCoord >= imagMax; imagCoord += imagStep) { //Two for Cyclic processing of a point in an image. N Specify a value. for (realCoord = realMin; realCoord <= realMax; realCoord += realStep) { //initialize variable iterations = 0; realTemp = realCoord; imagTemp = imagCoord; arg = (realCoord * realCoord) + (imagCoord * imagCoord); //2 It's the square root of 4, so it's only calculated. x^2+y^2 Value,while Loop execution iteration, while ((arg < 4) && (iterations < 40)) { //N*N-N Real part realTemp2 = (realTemp * realTemp) - (imagTemp * imagTemp) - realCoord; //N*N-N The imaginary part of imagTemp = (2 * realTemp * imagTemp) - imagCoord; realTemp = realTemp2; arg = (realTemp * realTemp) + (imagTemp * imagTemp); //The value of the current point is stored in iterations in iterations += 1; } //Select the character to be output switch (iterations % 4) { case 0: Console.Write("."); break; case 1: Console.Write("o"); break; case 2: Console.Write("O"); break; case 3: Console.Write("@"); break; } } //The inner loop ends with a line, so the newline character is output. Console.Write("\n"); } //Current boundary value Console.WriteLine("Current limits:"); Console.WriteLine("realCoord:from {0} to {1} ", realMin, realMax); Console.WriteLine("imagCoord:from {0} to {1} \n", imagMin, imagMax); //Enter a new boundary value Console.WriteLine("Enter new limits:"); //real number Console.WriteLine("realCoord:from:"); realMin = Convert.ToDouble(Console.ReadLine()); Console.WriteLine("realCoord:to:"); realMax = Convert.ToDouble(Console.ReadLine()); //Imaginary number Console.WriteLine("imagCoord:from:"); imagMin = Convert.ToDouble(Console.ReadLine()); Console.WriteLine("imagCoord:to:"); imagMax = Convert.ToDouble(Console.ReadLine()); } } }
Original boundary (-0.6, 1.2) (1.77, -1.2)
Existing boundary (-0.6,1.2) (0,0)
It's equivalent to enlarging a part of the original image: probably this part? At present, we can only understand this degree.