🌕 Write before
- 🍊 Blog Home Page: The Background of kikoking's Rivers and Lakes
- 🎉 Welcome to your attention 🔎 Give the thumbs-up 👍 Collection ⭐ Message 📝
- 🌟 This article was originally created by kikokingzz and started by CSDN!
- 📆 Start time: 🌹 02 December 2021 🌹
- 🆕 Latest update time: 🎄 02 December 2021 🎄
- ✉️ Persistence and hard work will surely exchange poems and distant places!
- 🙏 Author's level is limited, if you find a mistake, please leave a message to bomb! Thank you so much!
- Previous introduction:
- First, a thorough understanding of the logical structure-storage structure in the data structure
- Second, a thorough understanding of data structures and algorithm complexity
- Third, 408 Must See Order Table. Life is not "Order Table"
- Fourth, data structure must look at. Is this the single-chain list?
- C Language. Chain List Foundation Must Brush 21 Questions - Triple Hammer (Top)

Catalog
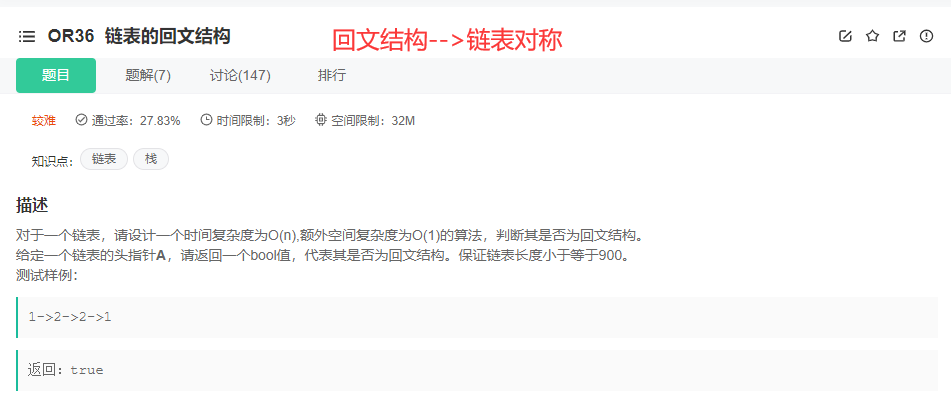
📄 Topic 7. Palindrome Structure of Chain Lists
✅ Idea 1: Pointer moves from end to middle
✅ Idea 3: Find intermediate node + backward inversion
📄 Question 8. Intersect Chain List
✅ Idea 1: Use fast and slow pointers
📄 Questions on this topic - > Interview Extensions
📄 Topic 10. Ring Chain Table II
✅ Idea Two: Variant Representation of Intersecting Chain Lists
📄 Question 11. Copying a chain table with random pointers
✅ Idea 1: Copy node links behind
📄 Question 12. Inserting and sorting chains
📄 Question 13. Removing duplicate nodes from a list of chains
✅ Idea 1: Multi-pointer problem
📄 Topic 7. Palindrome Structure of Chain Lists
✅ Idea 1: Pointer moves from end to middle
Pointers on both sides point to the same element -->Walk in the middle
However, because it is a single-chain list, the tail pointer cannot be moved backwards! Arrays can do this! Failed!
✅ Idea two: Open an array
Open an int a[900], put the data of the chain table into an array, and use the array to judge ----------------------> Spatial Complexity O(N)
✅ Idea 3: Find intermediate node + backward inversion
1. Find the middle node first---->Fast and slow pointers
2. Inverse second half--->

3. Comparison with the second half
//Find middle node, fast slow pointer
struct ListNode* middleNode(struct ListNode* head){
struct ListNode *fast = head, *slow = head;
while(fast&&fast->next)
{
slow=slow->next;//slow take a step
fast=fast->next->next;//fast takes two steps
}
return slow;
} //Invert Chain List Using Head Interpolation
struct ListNode* reverseList(struct ListNode* head){
struct ListNode* cur=head , *newHead=NULL;
while(cur)
{
struct ListNode* next=cur->next;
cur->next=newHead;
newHead=cur;
cur=next;
}
return newHead;
}/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
bool chkPalindrome(ListNode* A) {
struct ListNode* mid=middleNode(A);//Finding intermediate nodes
struct ListNode* rhead=reverseList(mid);//Invert the subsequent elements of the intermediate node
while(A&&rhead)//Comparison of two groups of elements, one ending
{
if(A->val!=rhead->val)
return false;
else
{
A=A->next;
rhead=rhead->next;
}
}
return true;
}
};
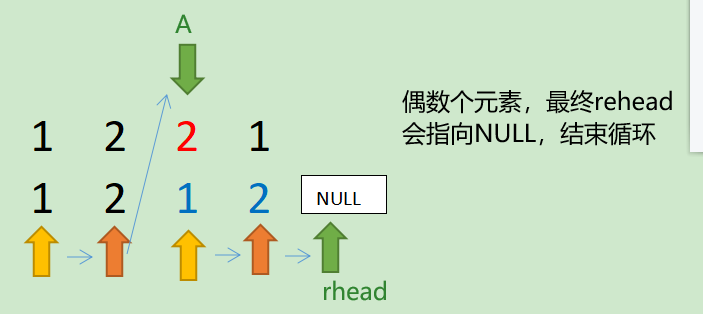
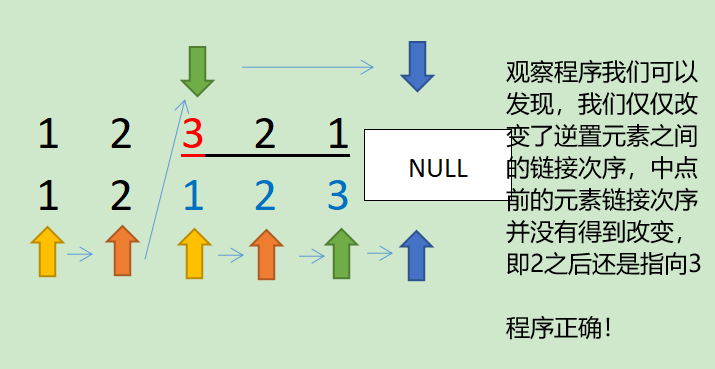
Successfully run, but I don't know if you found one thing carefully. According to the code of the Compare program, we can find that the comparison of even numbers is easy to understand. rehead will be empty and jump out of the program at the end, but for odd numbers, why can we skip?
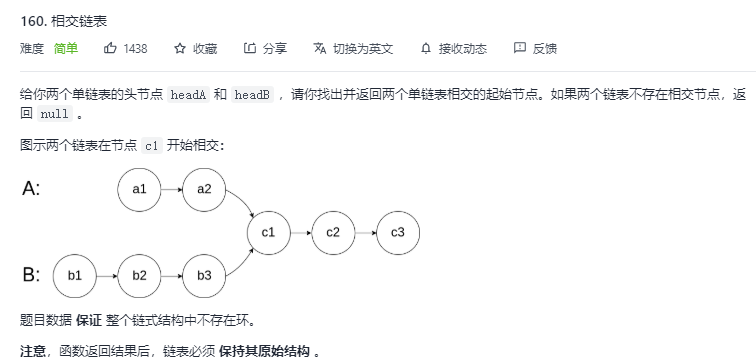
📄 Question 8. Intersect Chain List
For this topic, intersection can only be the case in the following picture, so can be seen in the title given!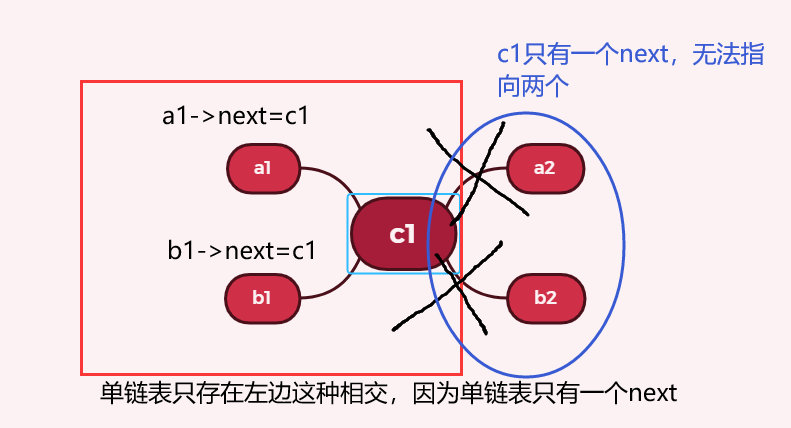
✅ Idea One
Q: Determine if two linked lists intersect
Find out if the addresses of nodes in two linked lists are identical
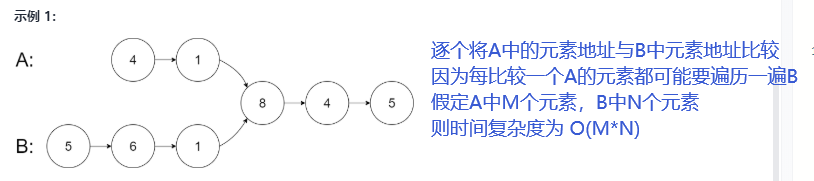
This method is a bit time-complex and is not recommended
✅ Idea Two
Q: Determine if two linked lists intersect
step1. Compare tail pointers
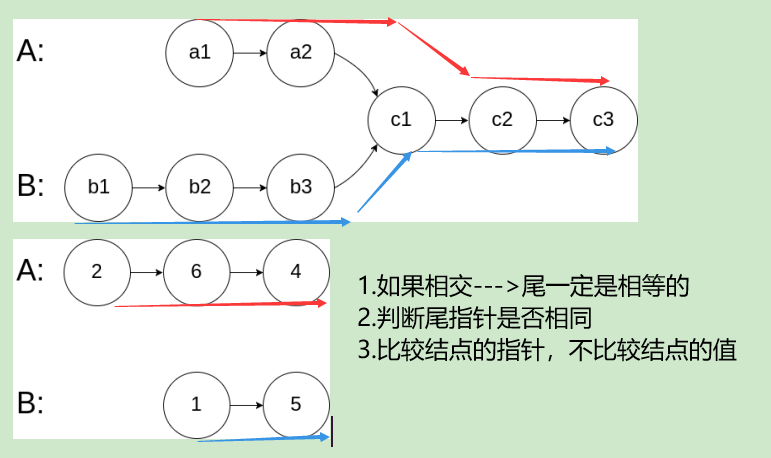
step2. If they intersect, find the intersection point
1. Calculate the lengths of the two chains so that the long chains can take the gap step first
2. Walk at the same time, the first identical node is the intersection
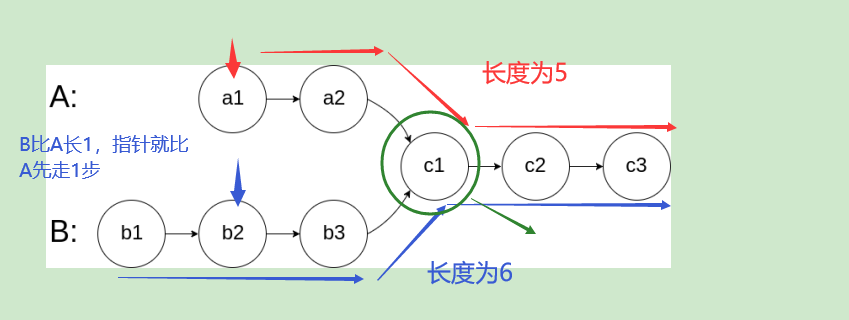
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
if(headA==NULL||headB==NULL)//If there is an empty list, it must not intersect
{
return NULL;
}
struct ListNode* curA=headA, *curB=headB;
int lenA=0,lenB=0;
while(curA->next)//Traverse all the way to the last node
{
curA=curA->next;//curA may be a null pointer, add judgment above
lenA++;
}
while(curB->next)
{
curB=curB->next;
lenB++;
}
//Disjoint-
if(curA!=curB)
return NULL;
//Long walk first, then at the same time
struct ListNode* longlist=headA, *shortlist=headB;//Assume A long B short
if(lenB>lenA)//If B is long A is short
{
longlist=headB;
shortlist=headA;
}
int gap = abs(lenB-lenA);//abs takes absolute value
while(gap--)//Gap--take the gap step
{
longlist=longlist->next;
}
printf("1");
while(longlist!=shortlist)
{
shortlist=shortlist->next;
longlist=longlist->next;
}
return shortlist;
}
📄 Question 9. Ring Chain List
141. Ring Chain List https://leetcode-cn.com/problems/linked-list-cycle/
https://leetcode-cn.com/problems/linked-list-cycle/
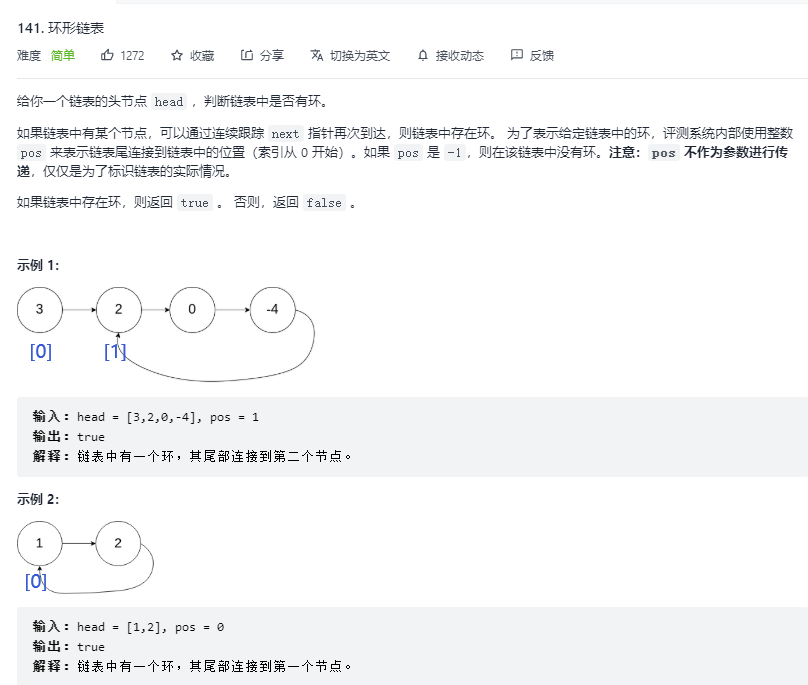
✅ Idea 1: Use fast and slow pointers
1.Fast pointer-->Take two steps at a time
2.Slow pointer slow-->One step at a time
3. If you have a ring, slow and fast will meet in the ring
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool hasCycle(struct ListNode *head) {
struct ListNode* slow=head, *fast=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;//fast takes two steps
if(slow==fast)
{
return true;
}
}
return false;
}
📄 Questions on this topic - > Interview Extensions
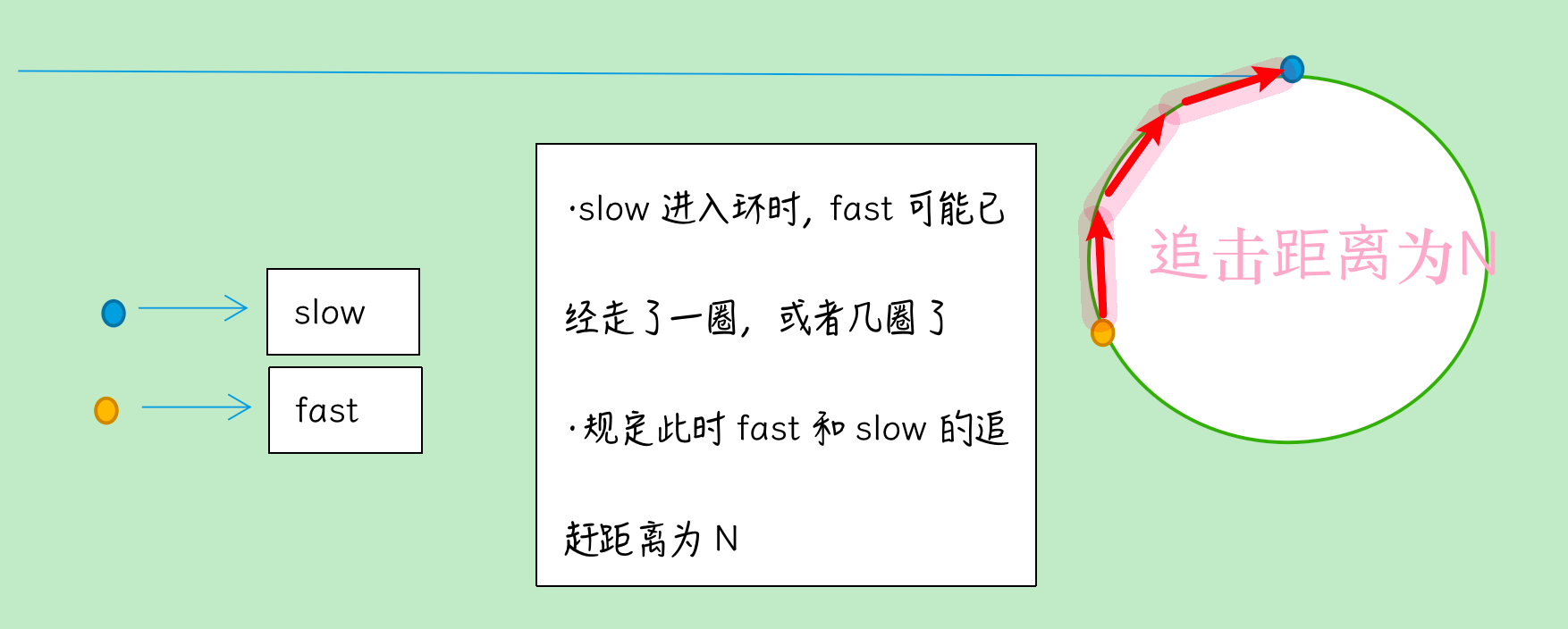
1. Why do slow and fast take one step and two steps? They will meet in the ring. Will they never catch up?
Proof: fast must already be in the ring when slow enters the ring. Assume that when slow enters the ring, the distance between fast and slow is N (fast follows slow, followed by N steps). For each step of slow, fast takes two steps forward and reduces the distance by one step. That is, slow takes N steps, the distance between fast and slow decreases N, and finally meets.
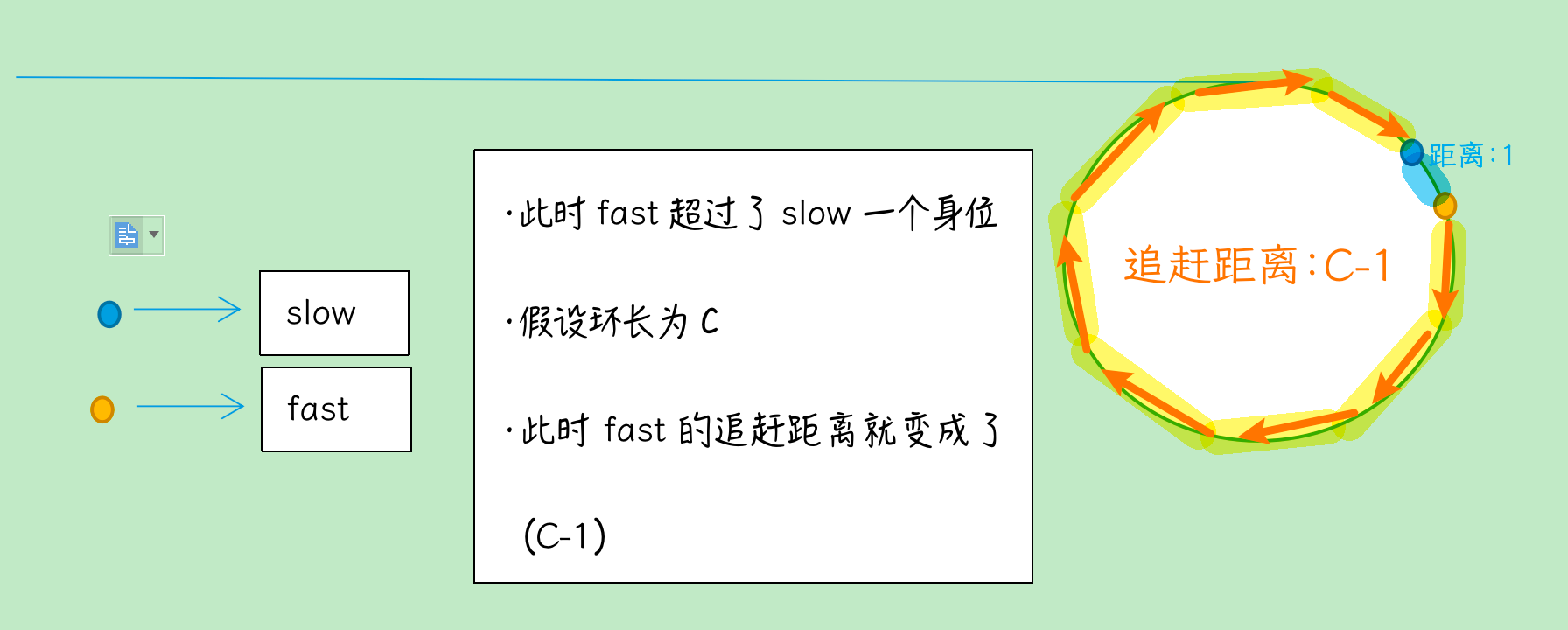
2.slow one step, fast three? Why?
Proof: every step of slow, every 3 steps of fast, every 2 steps of distance reduction, for distance N, only N is even, then they will meet, but if N is odd, they will miss. Assuming the ring length is C, the gap between fast and slow becomes (C-1) when it is missed. If C-1 is odd, then slow and fast never meet, because the distance reduction between slow and fast is always an even number (2)
📄 Topic 10. Ring Chain Table II
142. Ring Chain List II https://leetcode-cn.com/problems/linked-list-cycle-ii/
https://leetcode-cn.com/problems/linked-list-cycle-ii/
✅ Thought one: Push formula

Q1: Why did Slow walk L+X? Can't slow walk a little longer to meet?
A1: Because fast will catch up with slow in one circle after it enters the ring, slow is L+X. If slow has already taken one circle, then fast has already taken two circles and already caught up!
Because of the fast pointer fast Is a slow pointer slow Move twice as far, so you can get
The formula is as follows:
2(L+X)=L+X+n*C
L+X=n*C
L=n*C-x
-------------------->From the above formula, it can be concluded that when a pointer moves from the point of intersection and a pointer moves from the point of beginning, they meet at the entry point.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
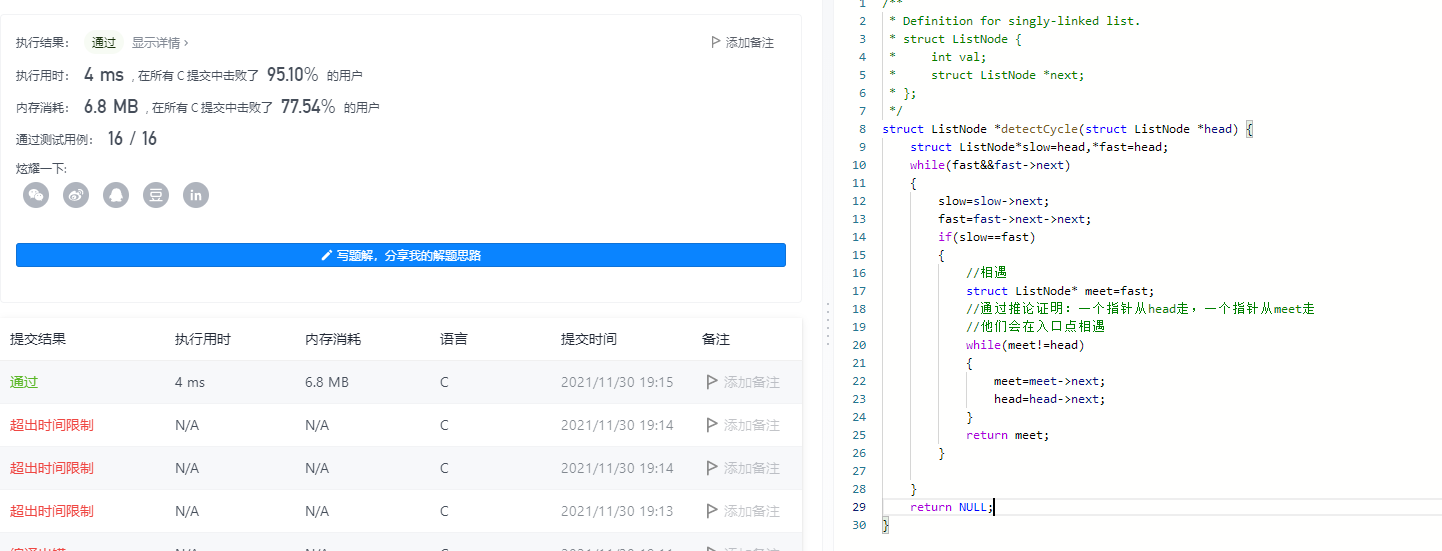
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode*slow=head,*fast=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
//meet
struct ListNode* meet=fast;
//The deduction proves that one pointer goes from head to meet
//They will meet at the entry point
while(meet!=head)
{
meet=meet->next;
head=head->next;
}
return meet;
}
}
return NULL;
}
✅ Idea Two: Variant Representation of Intersecting Chain Lists
📄 Question 11. Copying a chain table with random pointers

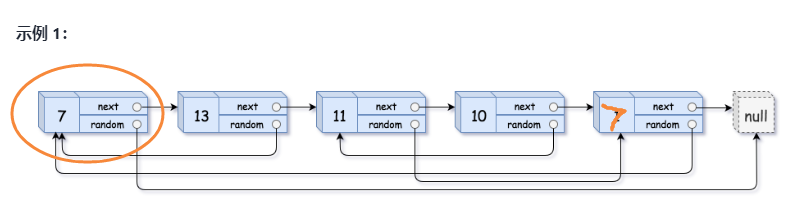
We can easily copy the next corresponding to each node, but the element that the random pointer points to is the difficulty of this problem.
Difficulty: random of copy nodes - too inefficient and complex to process
1. For example, in Example 1 above, the second node randomly points to 7, the new chain table does not know the address of 7, and needs to be traversed. The time complexity is O(N), so the time complexity to process each node randomly is O(N*N)
2. If there are many 7 in this list, the random 7 will not know which 7 it is, and the number of nodes with a value of 7 will need to be determined.
✅ Idea 1: Copy node links behind
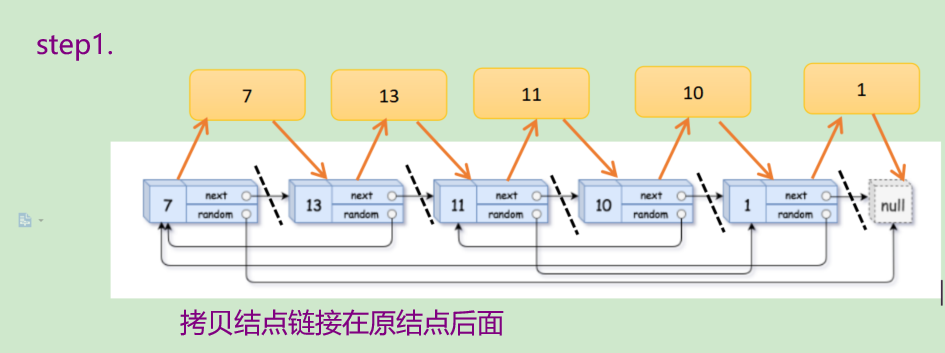
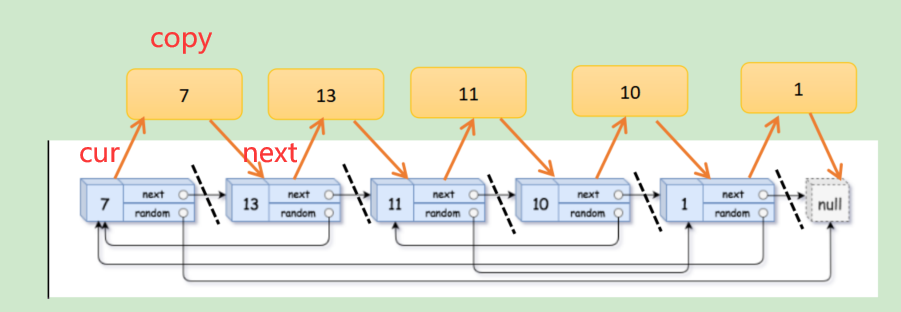
struct Node* copyRandomList(struct Node* head) {
//The step1 copy node is behind the origin node to establish the corresponding relationship
struct Node* cur=head;
while(cur)
{
struct Noed* next=cur->next;
struct Node* copy=(struct Node*)malloc(sizeof(struct Node));
copy-val=cur-val;
cur->next=copy
copy->next=next;
cur=next;
}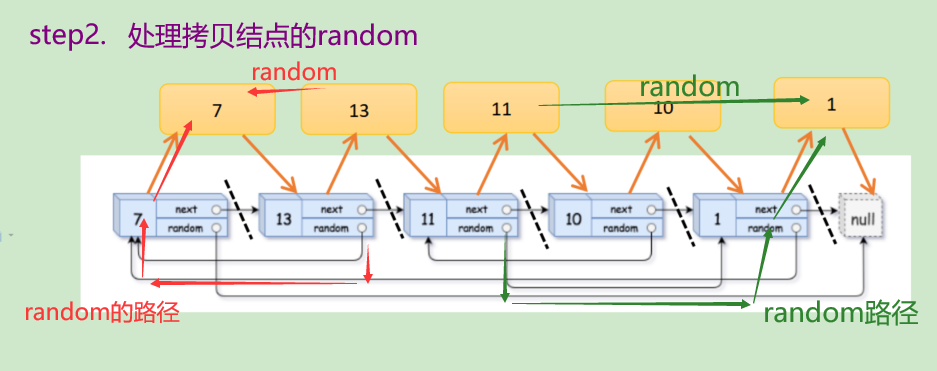
//step2. Processing random of copy nodes
cur=head;
while(cur)
{
struct Node*copy=cur->next;
if(cur->random==NULL)
{
copy->random=NULL;
}
else
{
copy->random=cur->random->next; //This sentence is the essence
}
cur=copy->next;
}🍓 The cleverness of the algorithm:
1. Make the copy random node behind the origin node by linking the copy node behind the origin node----->
2. So as long as you find the origin node that random ly points to, you will find the location of the copy node, avoiding searching in the new list of chains
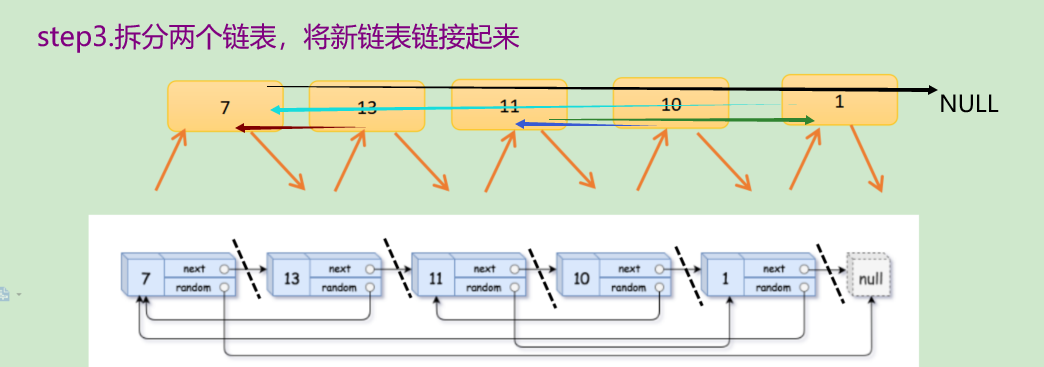
//step3. Remove the copy nodes and link them together to restore the original list
cur=head;
struct Node* copyHead, *copyTail;
copyHead=copyTail=(struct Node*)malloc(sizeof(struct Node));
//Sentry position for easy tail insertion
while(cur)
{
struct Node*copy=cur->next;
struct Node*next=copy->next;
//Tail insertion
copyTail->next=copy;
copyTail=copyTail->next;
cur->next=next;
cur=next;
}
struct Node*guard=copyHead;
copyHead=copyHead->next;
free(guard);
guard=NULL;
return copyHead;
📄 Question 12. Inserting and sorting chains
147. Insertion sort of chain table https://leetcode-cn.com/problems/insertion-sort-list/
https://leetcode-cn.com/problems/insertion-sort-list/
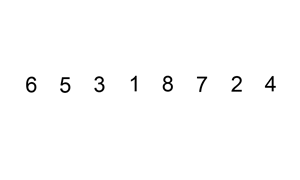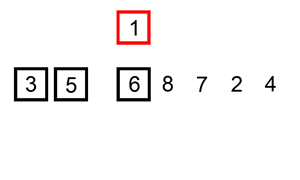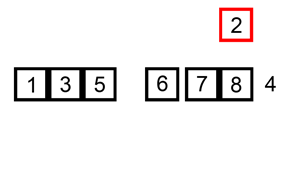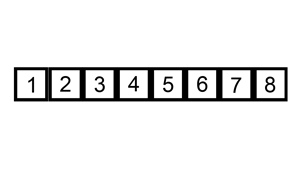

✅ Idea One
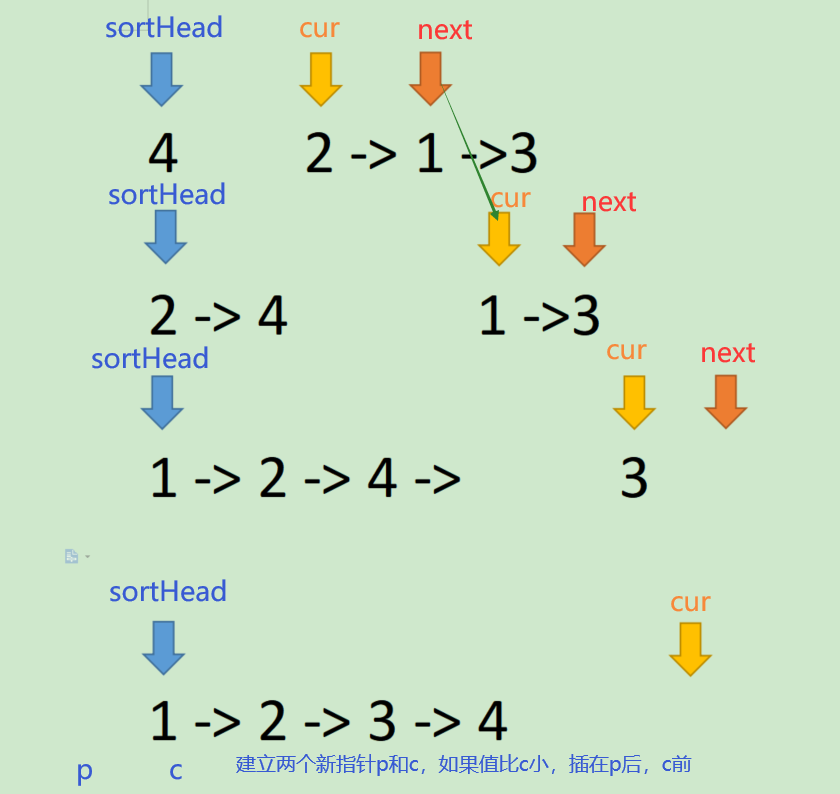
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* insertionSortList(struct ListNode* head){
if(head==NULL||head->next==NULL)
return head;
struct ListNode* sortHead = head;
struct ListNode* cur = head->next;
sortHead->next=NULL;
while(cur)//2. Termination Conditions
{
//3. Iteration Conditions
struct ListNode*next=cur->next;
//Interpolate cur nodes into the preceding ordered interval
struct ListNode* p=NULL, *c=sortHead;
while(c)
{
if(cur->val<c->val)
{
break;
}
else
{
p=c;
c=c->next;
}
}
if(p==NULL)
{
cur->next=c;
sortHead=cur;
}
else
{
p->next=cur;
cur->next=c;
}
cur = next;
}
return sortHead;
}
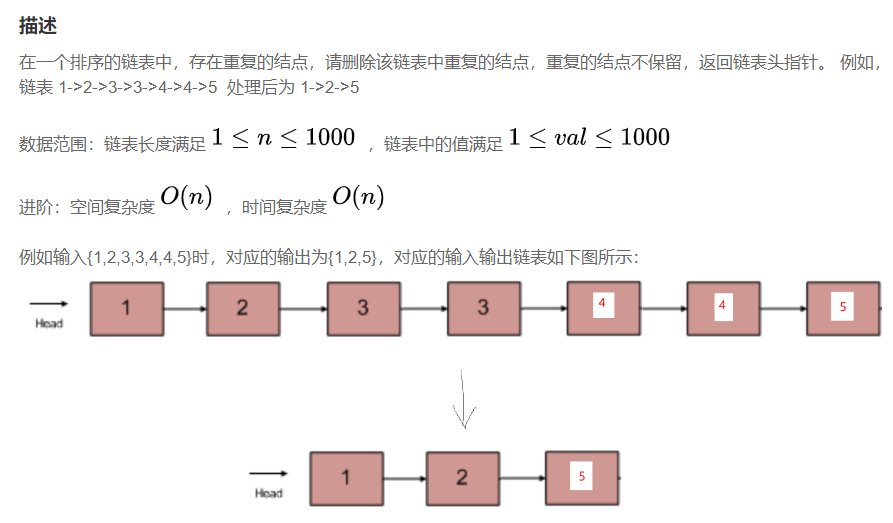
📄 Question 13. Removing duplicate nodes from a list of chains
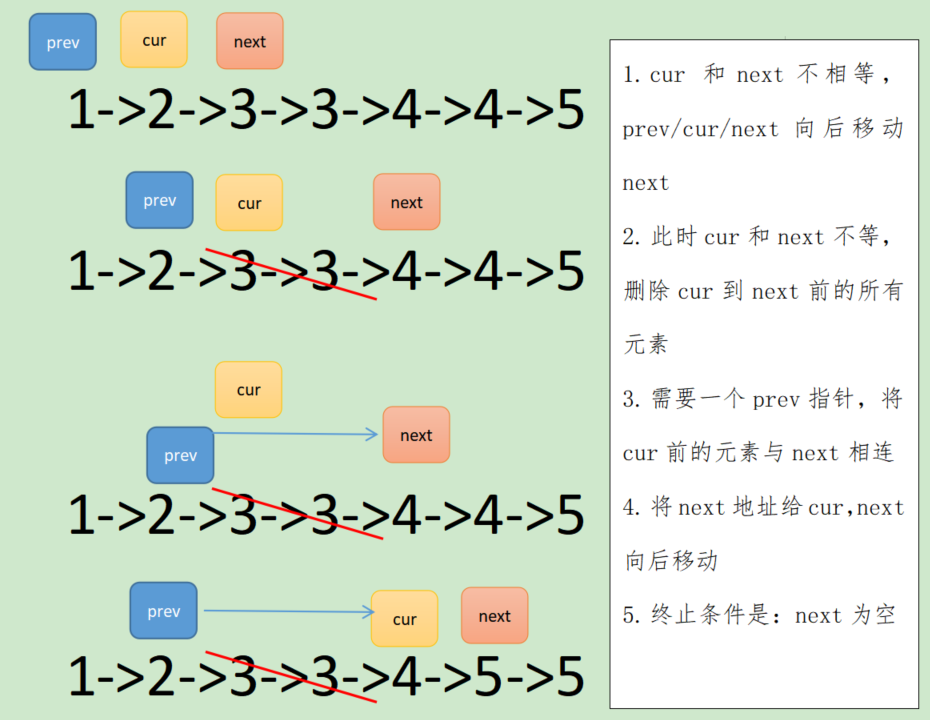
✅ Idea 1: Multi-pointer problem
Delete Problem-->Delete Duplicates-->Double Pointer Problem
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*
* C Language declaration defines global variables. Add static to prevent duplicate definitions
*/
/**
* The class name, method name and parameter name in the code have been specified. Do not modify them, just return to the value specified by the method.
*
*
* @param pHead ListNode class
* @return ListNode class
*/
struct ListNode* deleteDuplication(struct ListNode* pHead ) {
if(pHead==NULL||pHead->next==NULL)
return pHead;
struct ListNode* prev=NULL,*cur=pHead,*next=pHead->next;
while(next)
{
if(cur->val==next->val)
{
//Remove duplicates
while(next && cur->val==next->val)//To prevent null pointers, use the operator's short-circuit effect
{
next=next->next;
}
//Delete the node cur to next
while(cur!=next)
{
struct ListNode* del=cur;
cur=cur->next;
free(del);
}
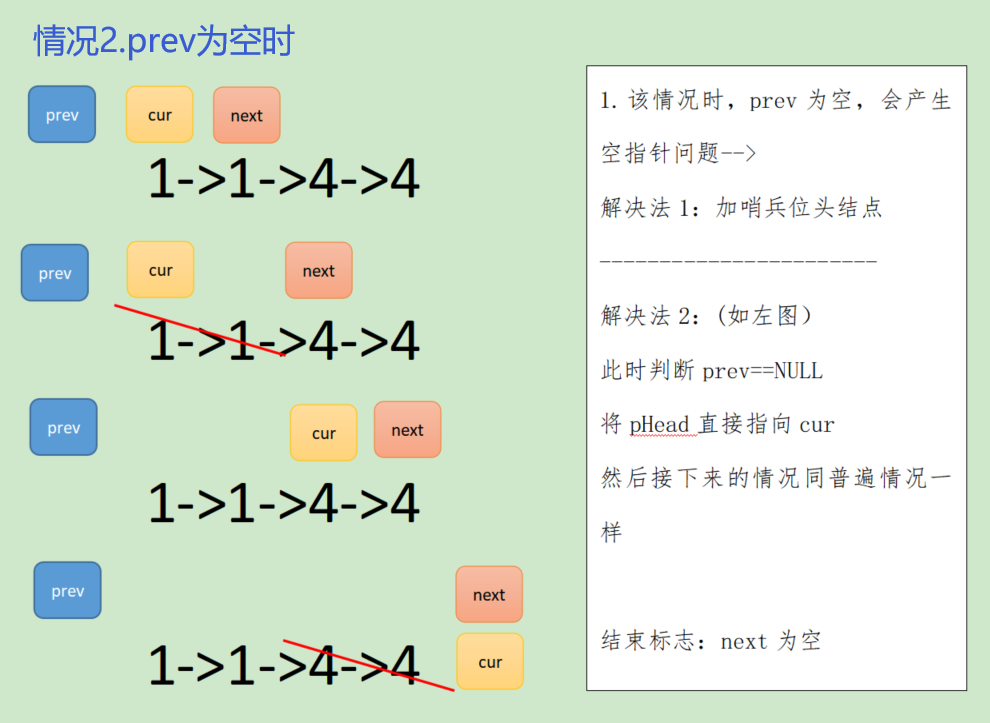
if(prev==NULL)
{
pHead=cur;
}
else
{
prev->next=cur;
}
if(next)
{
next=next->next;
}
}
else
{
//Move back at the same time
prev=cur;
cur=next;
next=next->next;
}
}
return pHead;
}