Data structures: trees

1, Tree

1. Definition of tree

A set composed of N nodes, n=0 is called an empty tree, and a tree with n=1 has only one node. For a tree with n > 1, T has:

• The top node is called the root node, and the root node has no precursor node
• Except for the root node, the other nodes are divided into m disjoint sets, and each set is a subtree with a structure similar to the tree

Common terms:

• Node degree: the number of subtrees (or child nodes) owned by a node
• Leaf node: degree 0 (no subtree)
• Degree of tree: the maximum degree of all nodes
• Branch node: a node whose degree is not 0 is called a branch node
• Child node: the root node of the subtree of a node in the tree
• Parent node: the precursor node of child node
• Sibling node: a node with the same parent node
• Node hierarchy: if the hierarchy of the root node is specified as 0, the hierarchy of other nodes is its parent node hierarchy + 1
• Depth of tree: the maximum value of node hierarchy. A tree with hierarchy 0 has only one root node
• Tree height: tree depth + 1
• Ordered tree: the order of sibling nodes from left to right cannot be interchanged
• Forest: a collection of trees

2. Common properties of trees

① Number of nodes = total degree of nodes + 1

The degree of the node represents how many children the node has. The root node is not included, so + 1

② Number of degrees M: the maximum degree representing one of the nodes is m

M-ary tree: the maximum degree of the representative node is m

③ The tree with degree m has at most mi nodes in layer i (the root node is layer 0)

④ The m-ary tree with height h has at most mh-1/m-1 nodes

• The m-ary tree with depth h has at most mk+1-1/m-1 nodes

⑤ The minimum height of M-ary tree with m nodes is [logm(n(m-1)+1)]

3. Abstract data type of tree

① Data set

The node set of the tree. Each node is composed of data elements and pointers that construct the relationship between data elements

② Operation set

Initiate(T);//initialization
Parent(T,curr);//Return parent node or NULL
LeftChild(T,curr);//Return left sibling node
RightChild(T,curr);//Return to the right sibling node
Traverse(T,Visit());//Preorder traversal
DestroyTree(T);//Undo tree

4. Storage structure of tree

① Parental representation

• Sequential storage
• A node stores two contents, data and parent

② Child representation

• Sequence + Chain
• The nodes are stored sequentially, that is, data, and the first child is stored in a chain

③ Child brother representation

• Chain type
• Similar to chain storage binary tree
• The successor nodes of each node are the first child and the brother node

5. Forest and binary tree transformation

① Forest 👉 Binary tree

Connect the root node with the right pointer. If there are trees X,Y,Z (representing the node tree) into a binary tree, take the root node of X as the root node, connect y with the right pointer, and then connect Z with the right pointer of Y, then the total number of right subtrees is Y+Z and the total number of left subtrees is X-1.

② Binary tree 👉 forest

On the contrary, the right subtree is separated from the bottom layer to the root node

2, Binary tree

1. Definition of binary tree

Binary tree is not a special case of tree. Tree and binary tree are two different types of tree structure

• n=0: empty binary tree
• n=1: only one root node
• n> 1: it is composed of one root node and at most two disjoint sub binary trees called left subtree and right subtree respectively

Full binary tree: all branch nodes have left subtree and right subtree. All leaf nodes are on the same layer. If the depth is k, there is a binary tree with 2k+1-1 nodes

• Only the last layer has leaf nodes
• There is no node with degree 1
• Numbering from 1 in sequence, the left child of node i is 2i, the right child is 2i+1, and the parent node of node i is [i/2]

Complete binary tree: it is called complete binary tree if and only if each node corresponds to the nodes numbered 1~n in the full binary tree with height h

• Only the last two layers may have leaf nodes
• For any node, the maximum level of descendants under its left branch is not less than the maximum level of descendants under its right branch
• There is at most one node with a degree of 1
• i ≤ [n/2] is a branch node, otherwise it is a leaf node

Binary sort tree: the root node of the left subtree is less than the keyword of the root node of the right subtree

Balanced binary tree: the depth difference between the left subtree and the right subtree of any node of the tree shall not exceed 1

2. Properties of binary tree

Binary tree

① Let the number of nodes in a non empty binary tree be 0, 1 and 2 respectively x, y and z, then x=z+1

• There is one more leaf node than two branch nodes (with both left and right children)

② There are at most 2i nodes (i ≥ 1) in layer i of binary tree

• There are at most mi-1 nodes (i ≥ 1) in layer i of m-ary tree

③ A binary tree with height h has at most 2h-1 nodes

• [mh+1-1]/[m-1]
• A binary tree with depth k has at most 2k+1-1 nodes

Complete binary tree

④ The height h of a complete binary tree with n nodes is [log2(n+1)] or [log2n]+1

• The level of the ith node is [log2(n+1)] or [log2n]+1

⑤ The depth of a complete binary tree with n nodes is log2(n+1)-1

⑥ For a complete binary tree, the number of nodes with degrees 0, 1 and 2 can be deduced from the number of nodes n, and the number of nodes is x, y and z

• A complete binary tree has at most one node with a degree of 1
• y is 0 or 1
• x=z+1 must be odd
• If a complete binary tree has 2k nodes, it must have x=1, y=k, z=k-1

⑦

• i's left child 2i, right child 2i+1
• Parent node of i/2
• Level of i log2(n+1) or log2n+1
• Judge whether i has left child: 2i ≤ n
• Judge whether i has a right child: 2i+1 ≤ n
• Judge whether i has a leaf / branch node: i > [n / 2]

3. Storage structure of binary tree

① Sequential storage

When the size and shape of binary tree do not change dramatically

② Chain storage

The binary list with n nodes has n+1 empty chain fields

typedef struct BiTNode
{ DataType data;
struct BiTNode *leftChild;
struct BiTNode *rightChild;
} BiTreeNode;

void Initiate(BiTreeNode **root)/*initialization*/
{ *root = (BiTreeNode *)malloc(sizeof(BiTreeNode));/ /Head node
(*root)->leftChild = NULL;
(*root)->rightChild = NULL;
}

BiTreeNode *InsertLeftNode(BiTreeNode *curr, DataType x)
/*Insert node x in the left subtree of curr node*/
{ BiTreeNode *s, *t; //s: Newly generated node pointer
if (curr == NULL) return NULL;  //Insert failed
t = curr->leftChild;  //Original left subtree
s = (BiTreeNode *)malloc(sizeof(BiTreeNode));
s->data = x;
s->leftChild = t;
s->rightChild = NULL;
curr->leftChild = s;  //New left subtree
return curr->leftChild;  //Insert successful
}

BiTreeNode *DeleteLeftTree(BiTreeNode *curr)
/*Delete the left subtree of curr node*/
{ if(curr == NULL || curr->leftChild == NULL)
return NULL;  //Deletion failed
Destroy(&curr->leftChild);  //To be stated
curr->leftChild = NULL;
return curr; //Delete succeeded
}

void main(void)
{  BiTreeNode *root, *p;
Initiate(&root);
p = InsertLeftNode(root, 'A');
p = InsertLeftNode(p, 'B');
p = InsertLeftNode(p, 'D');
p = InsertRightNode(p, 'G');
p = InsertRightNode(root->leftChild, 'C');
InsertLeftNode(p, 'E');
InsertRightNode(p, 'F');
}

4. First middle then order traversal of binary tree

First left then right, follow the name

① Preorder traversal (NLR)

For each subtree

First the root node, then the left node, and then the right node

② Medium order traversal (LNR)

For each subtree

First the left subtree, then the root node, and then the right node

③ Postorder traversal

For each subtree

First the left subtree, then the right subtree, and then the root node

5. Sequence traversal of binary tree

Left to right traversal layer by layer (queue assisted)

6. Constructing binary tree from traversal sequence

Given only one traversal order, a certain binary tree cannot be obtained. To determine a binary tree, at least:

• Front + middle

• Rear + middle

• Layer + middle

Find the corresponding combination and split it from top to bottom

• Confirm the root node and the nodes contained in the left and right subtrees
• Loop back

3, Binary sort / find / search (BST) tree

1. Definition

Left subtree node value < root node value < right subtree node value

Using middle order traversal, you can obtain an increasing ordered sequence

• Or an empty binary tree;
• Or a binary tree with the following properties: for the root node, set its value to K,
• Then the value of any node of the left subtree (if not empty) of the node is less than K;
• The value of any node of the right subtree (if not empty) of the node is greater than K; and
• And its left and right subtrees are also binary search trees.

2. Search algorithm of binary search tree

① Thought

• Starting from the root node, find k in the binary search tree.
• If the value of the root node is equal to k, the search succeeds and the search ends;
• If k is less than the value of the root node, you only need to find the left subtree of the root;
• If k is greater than the value of the root node, only the right subtree of the root is searched.
  This process continues until k is found (successful search) or a leaf node is encountered and k is still not found (failed search).
• If the search succeeds, the address of the queried node will be returned. If the search fails, NULL will be returned.
• The reason for the high efficiency of binary search tree is that only one of the two subtrees needs to be found.

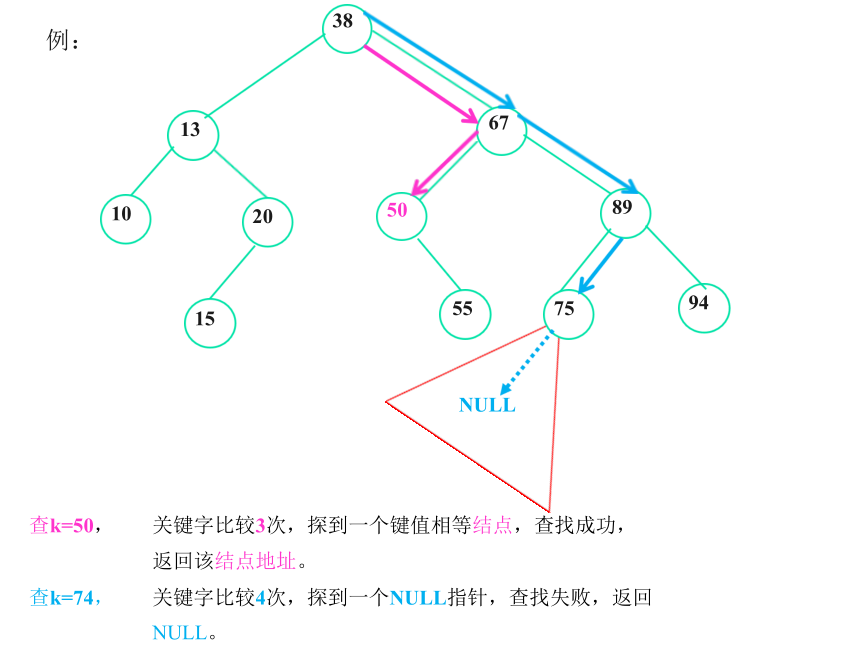
② Implementation (the latter is recursive)

BiTreeNode * SearchI(BiTreeNode * root, DataType item)
/*Find the item data element in the binary search tree with the root node as the root in an iterative form*/
{ BiTreeNode *current;
if (root!=NULL)
{  current=root;
while(current!=NULL)
{  if(item.key==current->data.key)
return current; /*Search succeeded*/
else if(item.key<current->data.key)
current=current->leftChild;
else current=current->rightChild;
}
}
return NULL; /*Search failed*/
}

BiTreeNode * Search(BiTreeNode * p, DataType item)
/*Find item data elements recursively in the binary search tree with p node as root*/
{ if (p==NULL)
return NULL; //base case 1: search failed, no recursion, return 1?
if( item.key==p->data.key)
return p; //base case 2: the search is successful without recursion, and returns 2?
else if( item.key<p->data.key)
return Search(p->leftChild, item); //Recursion, return 3?
else return Search(p->rightChild, item);} //Recursion, return 4?

③ Performance analysis

The maximum comparison times of binary search tree depends on the height O(h) of the tree

• A single tree is formed during orderly insertion. This is the worst case. The time required for tree search, insertion and deletion is O(n).
• u in the random case, the average time of search, insert and delete operations is O(logn).

3. Insertion of binary search tree

The insertion is carried out as follows:

• First, find the item node in the binary search tree.
• If the search fails, the insertion position parent is obtained.
  Generate a new node, and set the data field of the new node as item.
• If the binary search tree is empty, the new node is the root node of the binary search tree.
• If the binary search tree is not empty, compare the value of the new node with the keyword value of the parent:
  • If it is less than the value of the parent node, the left child as the parent is inserted
  • If it is greater than the value of the parent node, the right child as the parent is inserted

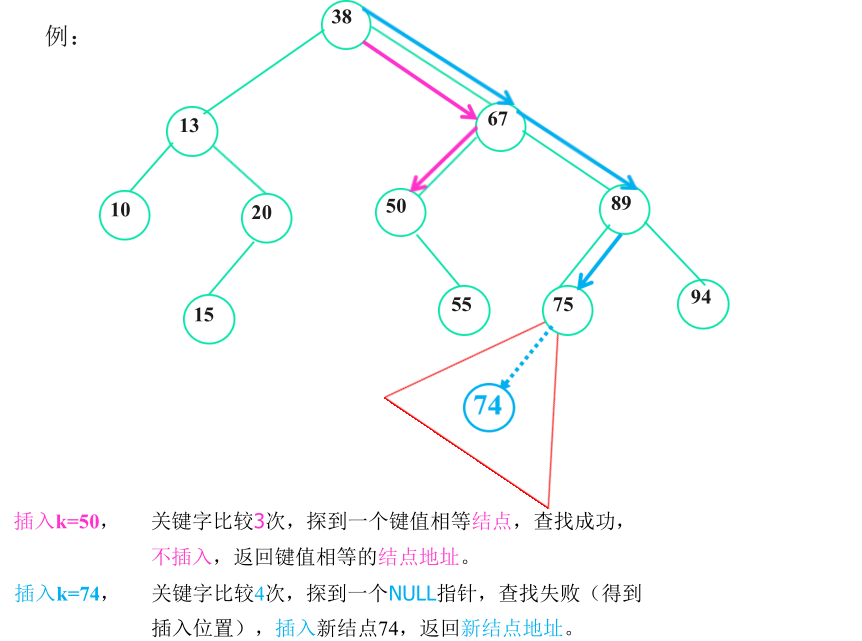
BiTreeNode * InsertI(BiTreeNode **root, DataType item)
/*Insert a new item node iteratively in the binary search tree with root as the root pointer*/
{ BiTreeNode *current,*parent=NULL,*p;
current =*root;
while(current!=NULL)
{ if(item.key== current->data.key) return NULL; /*The search succeeded without inserting*/
parent= current;
if(item.key>current ->data.key)
current = current ->rightChild;
else current = current ->leftChild;
}
p=(BiTreeNode *)malloc(sizeof(BiTreeNode));
p->data=item; p->leftChild=p->rightChild=NULL;
if (parent==NULL) *root=p; /*The binary search tree is empty and p is the root node*/
else if(item.key<parent->data.key) parent->leftChild=p;
else parent->rightChild=p; /*Insert p node*/
return p; /*Successfully inserted*/
}

BiTreeNode * Insert(BiTreeNode * p, DataType item)
{ if (p==NULL) /*base case 1: Search failed, insert, no recursion, return 1?*/
{ q=(BiTreeNode *)malloc(sizeof(BiTreeNode));
q->data = item; q->leftChild = q->rightChild = NULL;
return q; } /*When will the connection be established?*/
if ( item.key < p->data.key)
p->leftChild=Insert(p->leftChild,item); //Recursion, establish connection after return
else
if ( item.key > p->data.key)
p->rightChild=Insert(p->rightChild,item);//Recursion, establish connection after return
return p; }/*base case 2: If the search is successful, no insertion, no recursion, return 2?*/

3. Deletion of binary search tree

The deleted node has the following three conditions:

• 1) The deleted node is a leaf node (the left and right subtrees are empty)
• 2) The deleted node has only one child node (the left subtree is empty or empty)
  Right subtree (empty)
• 3) The deleted node has two child nodes (both left and right subtrees)
  (not empty)

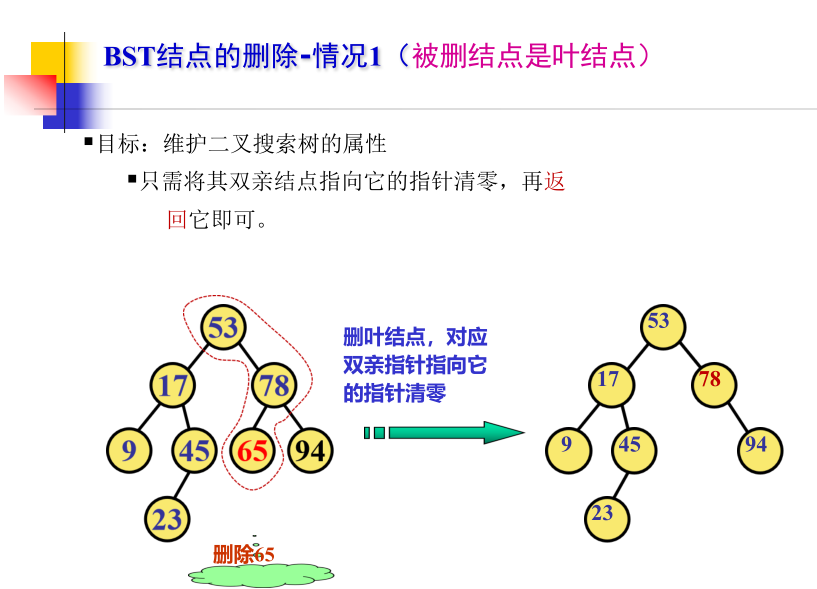
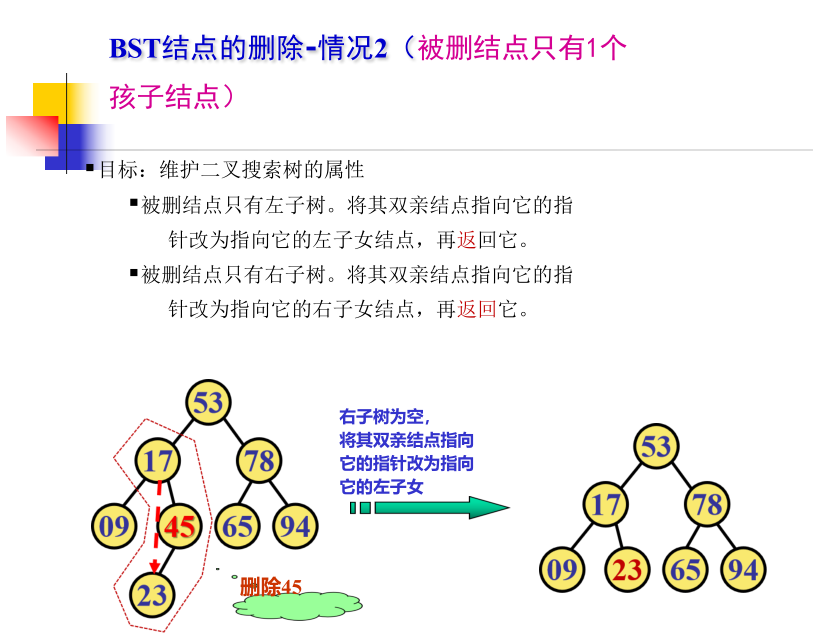
BiTreeNode* Remove ( BiTreeNode* p, DataType item)
{  //Recursive function: delete the node containing x in the binary search tree with ptr as the root,
//If the deletion is successful, the new root is returned through ptr.
BiTreeNode *replace,*temp;
if ( p == NULL ) //base case 1: NULL detected, deletion failed, no recursion, return 1:?
return NULL;
if ( item.key < p->data.key )
p->leftChild=Remove(p->leftChild, item); //Recursive - delete in the left subtree and establish a link after returning
else if ( item.key > p->data.key )
p->rightChild=Remove(p->rightChild, item); //Recursive - delete in the right subtree and establish a link after returning
else if ( p->leftChild && p->rightChild )
//Find the node with key x to be deleted, and the node has two children
{ replace= p->leftChild; /*Find avatar node in p left subtree*/
while( replace->rightChild!=NULL ) replace=replace->rightChild ;
p->data = replace->data; //The node data field is used to cover the ptr data field
p->leftChild=Remove ( p->leftChild, p->data); /*Recursion - on p right
 Delete the node with the same value as the p key in the subtree, and establish a link after returning*/
}
else {  /* p->data.key==item.key And p points to the avatar node to be deleted
 Only one or zero children*/
temp = p;  //temp points to the avatar node (i.e. the deleted node)
if ( p->leftChild == NULL ) / /p Down one floor
p = p->rightChild; //Only right children or zero children
else
p = p->leftChild; //Only left children
delete temp; //Delete avatar node
}
return p;  //base case 2: deletion succeeded, no recursion, return 2:?
}    

4, B-tree

1. Definition

If the keyword limit is set to m, each branch node can have at most M-1 keywords

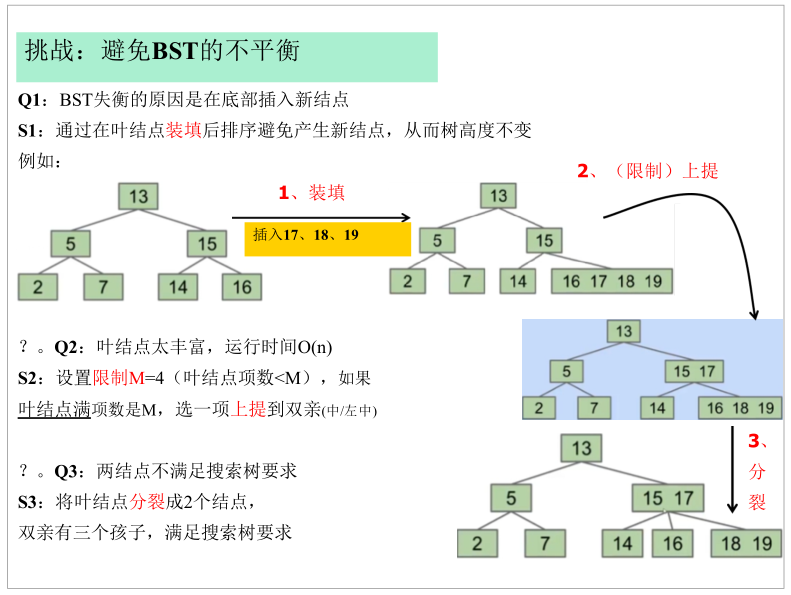
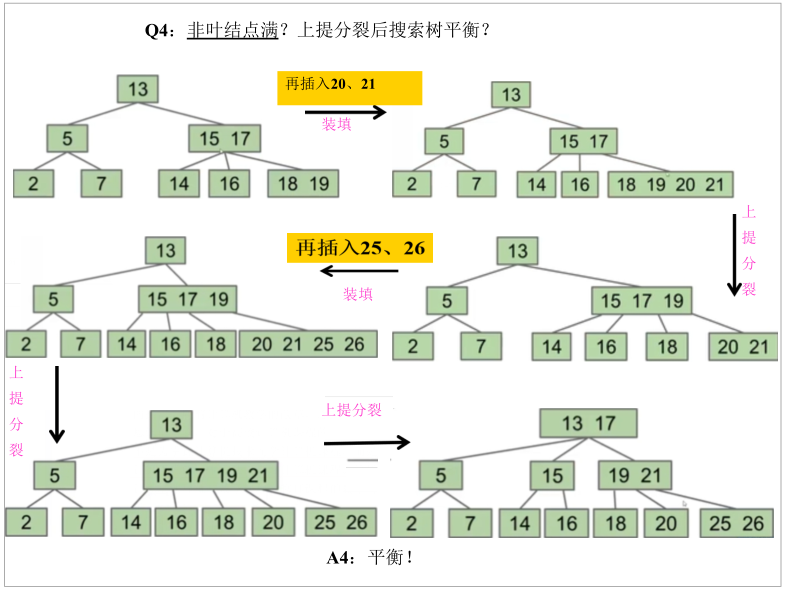
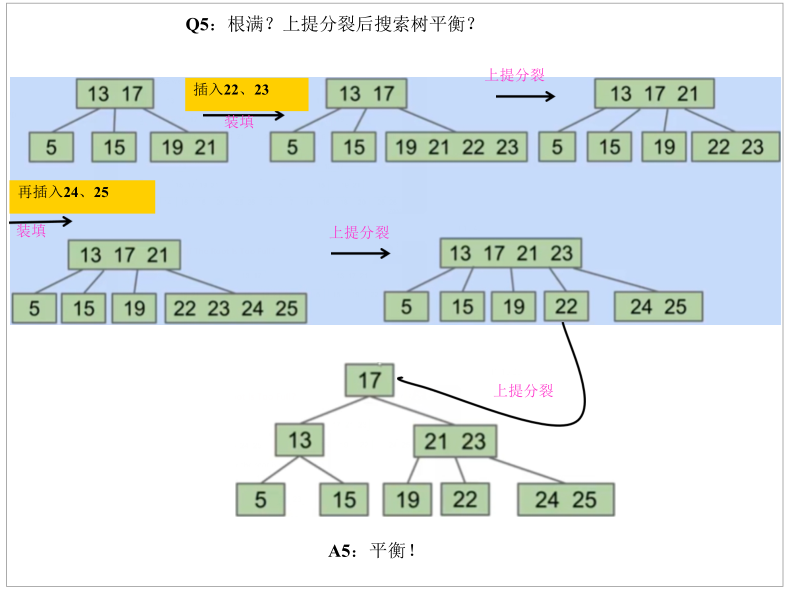
• When inserting, do not extend, first find the appropriate position and merge

• Lift up the middle position (or the first position in the middle) beyond the limit

• Then it is split and divided into different intervals according to the lifting, and each interval forms a subtree

• If the root node is full, continue to raise it to form a new root node

By splitting nodes in the middle, we can maintain a perfect balance! These trees are called B trees (M > 2) or 2-3-4 / 2-3 trees.

2. Invariant

• All leaves must be kept at the same distance from the root.
• Non leaf nodes with K terms must have exactly k+1 child nodes.

3. Performance analysis

The worst running time of search in B tree is that if the number of elements in each node is the largest, we must always traverse to the bottom. M is used to represent the number of subtrees in each node, and L=M-1 represents the number of elements in each node. This means that you will need to explore the logn node. And on each node, l elements will need to be explored. In short, we need to run the Llogn operation. However, m and L are constants, so our total running time is O(logn).

BST has the optimal height O(logn) and the worst-case height O(n)

B-tree is an improvement of BST, which avoids the worst case of O(n)

B tree has perfect balance. The run time of the operation is O(logn).

5, Red black tree

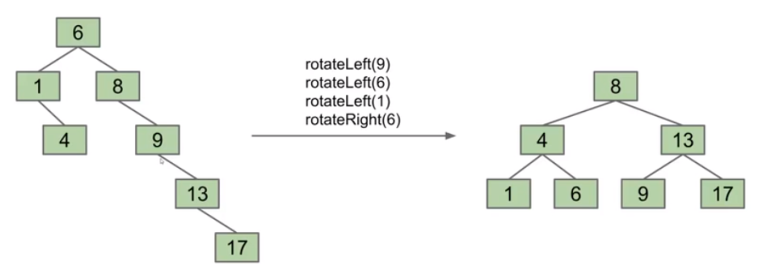
1. Rotation of BST tree

The rotation operation of BST is defined as:

• Rotate left (g): let x be the right child of G, so that G becomes the new left child of x.
• Rotate right (g): let x be the left child of G and make g the new right child of x.

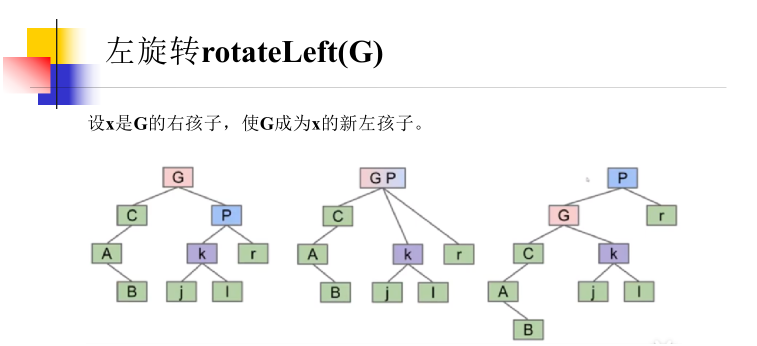
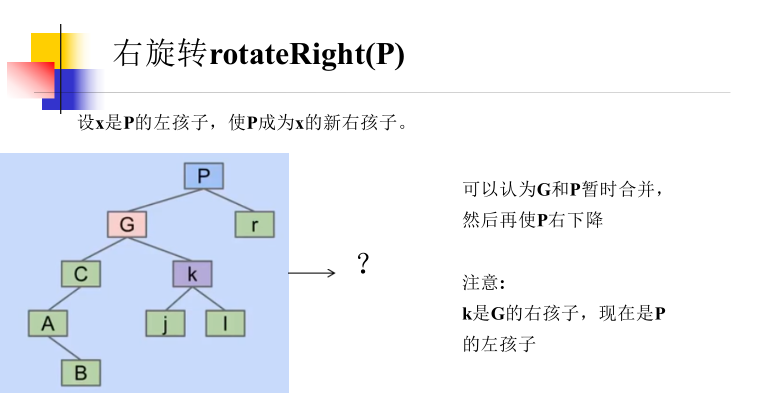
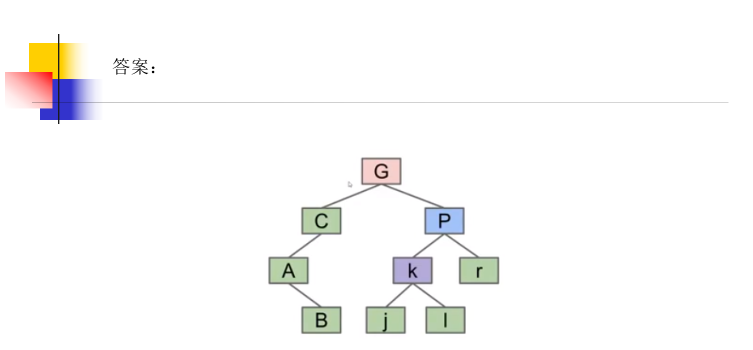
// Tilt right link to left
Node* rotateLeft(Node* h) {
// Suppose H= NULL && isRed(h->leftChild);
Node *x = h->rightChild;
h->rightChild = x->leftChild;
x->leftChild = h;
return x;
}//O(1)

//Tilt left link to right
Node* rotateRight(Node* h) {
// Suppose H= NULL && isRed(h->rightChild);
Node *x = h->leftChild;
h->leftChild = x->rightChild;
x->rightChild = h;
return x;
}//O(1)

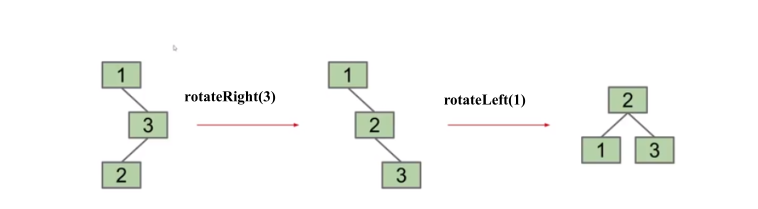
2. Red black tree definition

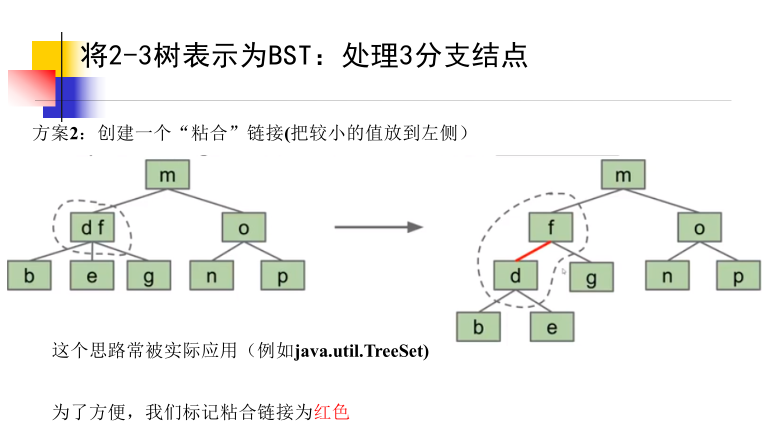
We choose to make the left element a child of the right element, which will cause the tree to tilt to the left. We show that the link is a glued link by turning it red, and the normal link is black. Therefore, we call these structures left leaning red black binary search tree (LLRB), which we will use in this course.

LLRB is a normal BST

• There is a 1-1 correspondence between LLRB and the equivalent 2-3 tree
• Red is just a convenient fiction. Red links have no special function

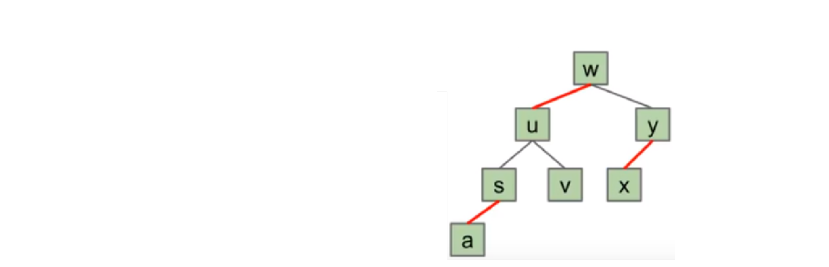
3. Properties of LLRB tree

• 1-1 corresponds to a 2-3 tree. LLRB has a 1-1 correspondence with 2-3 trees. Each 2-3 tree has a unique LLRB correspondence.
• No node has 2 red links (nodes with 2 red links are similar to nodes with 4 branches, but 2-3 trees are not allowed).
• There is no red right link.
• (black balance) each path from root to leaf has the same number of black links (because the number of links from 2-3 tree roots to each leaf is the same), so LLRB is balanced.
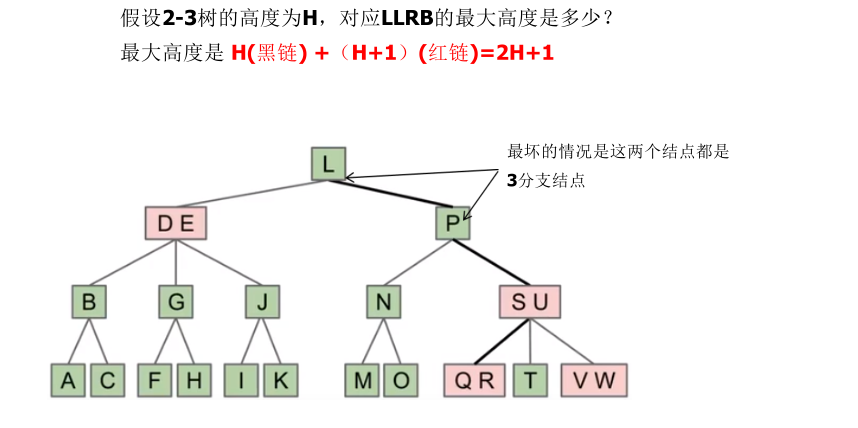
• The height shall not exceed 2 times of the corresponding 2-3 tree height.

[the external chain picture transfer fails, and the source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-j5oT4PKX-1625191541594)(C:\Users \ Leizi of Guan Er \ Desktop \ future village head \ picture \ image-20210701211944467.png)]

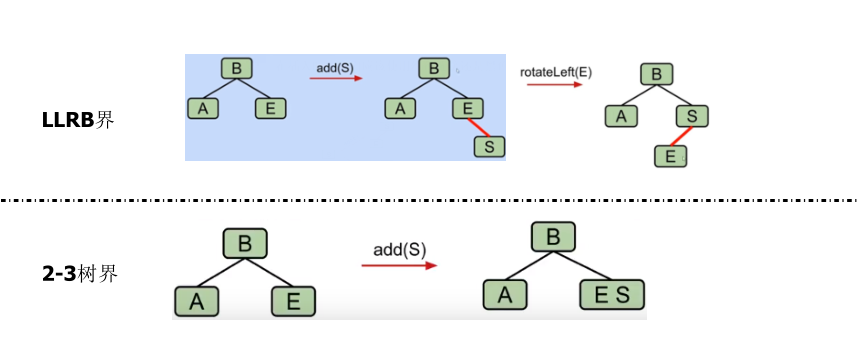
4. Split temporary 4 branch nodes

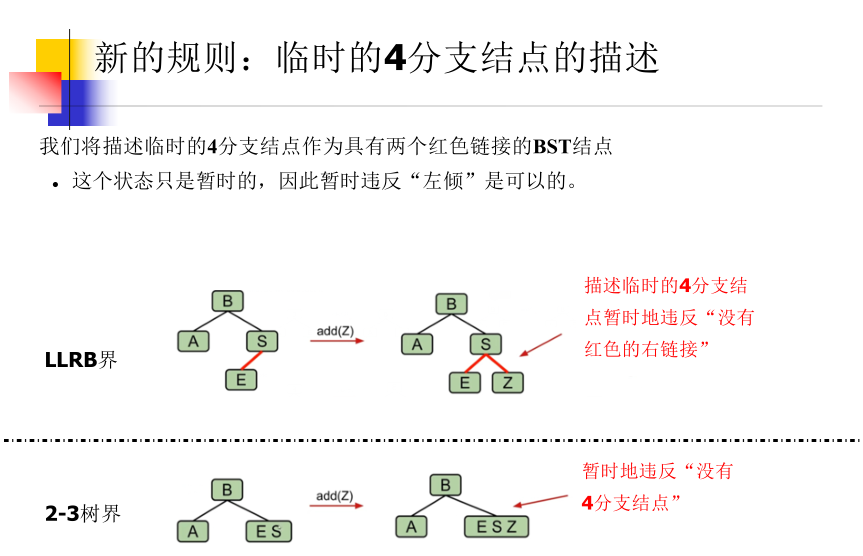
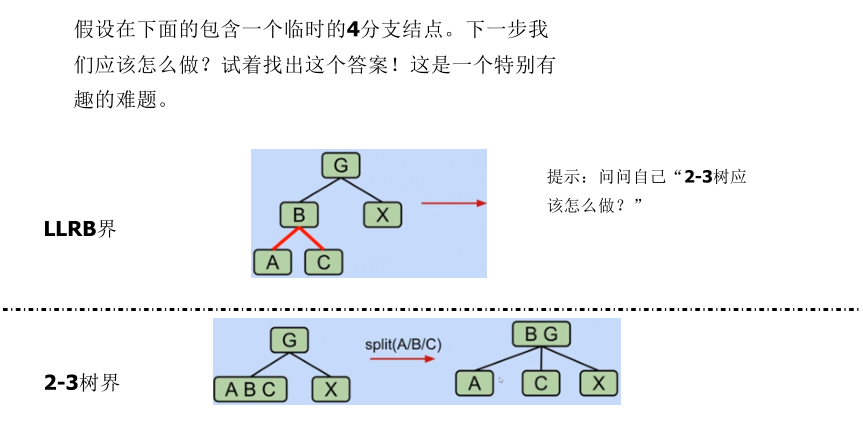
When inserting: use red link

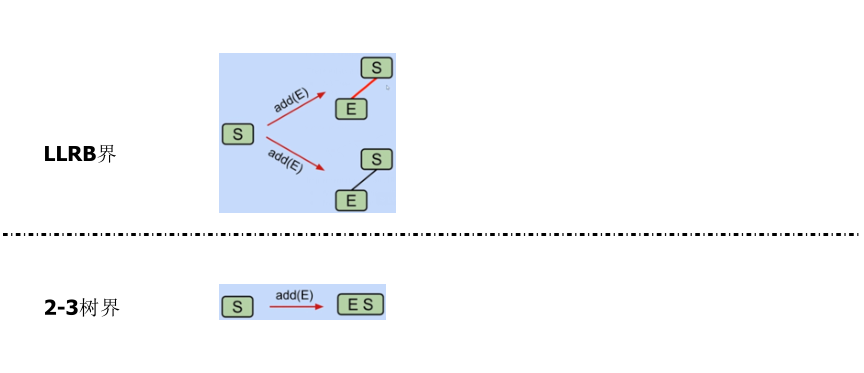
1. If there is a right leaning 3 branch node, we violate the "left leaning" rule!

• Rotate the corresponding node to the left

1. If there are two consecutive left links, we have an incorrect 4-node violation!

• Rotate the corresponding node to be repaired to the right

1. If any node has two red links, we violate the "No 4 branch node"
   "Point" rule!

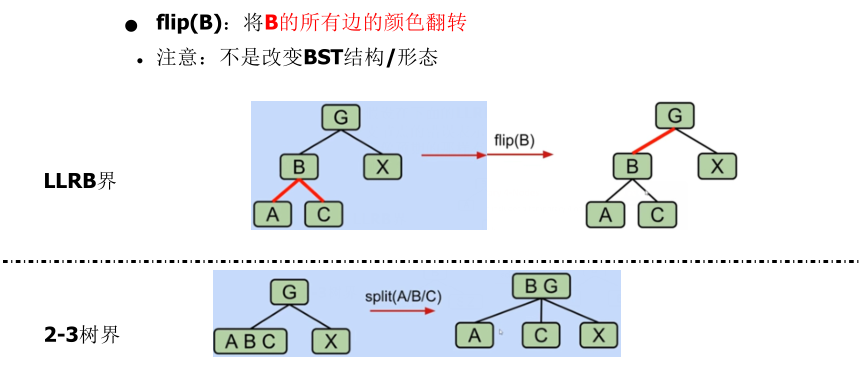
• Color flip the nodes to simulate the operation of splitting nodes

5. Cascade balance

Insert Z so that we have a 4-branch node
Color flipping produces an invalid tree. Why? What's next?
We have a right leaning 3-branch node (B-S node). We can use: rotateLeft(B) to repair it

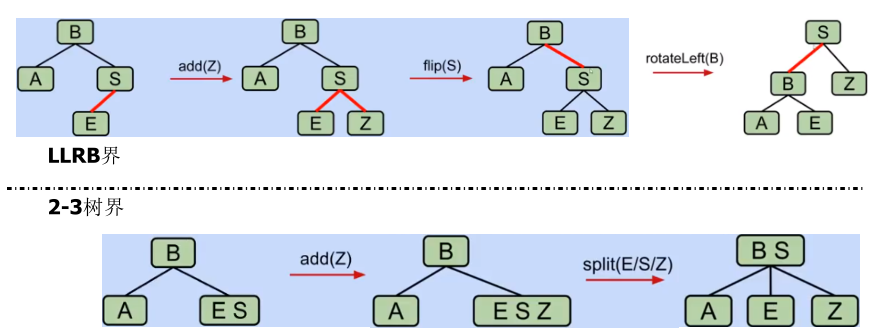
6. LLRB tree run time

Node put(Node *h, Key k, DataType d) {
if (h == null) { h=(Node *)malloc(sizeof(Node));h->data=d;h-
>key=k;h->color=RED); }
int cmp = compareTo(k, h->key);
if (cmp < 0) { h->leftChild = put(h->leftChild, k, d); }
else if (cmp > 0) { h->rightChild = put(h->rightChild, k, d); }
else { h->data = d; }
//Three lines of code
if (isRed(h->rightChild)&&!isRed(h->leftChild)){h=rotateLeft(h);}
if (isRed(h->leftChild)&&isRed(h->leftChild
->leftChild)){h=rotateRight(h); }
if (isRed(h->leftChild)&&isRed(h->rightChild)){ flipColors(h); }
return h; }

LLRB trees are easy to implement, but difficult to delete

6, Tree traversal

1. Depth first traversal

① Preorder traversal

1. Access the root node;
2. Pre order traversal of the left subtree;
3. The pre order traverses the right subtree.

void Print(DataType item)
//Write the corresponding access function according to the application needs
{ cout<< item; }
void PreOrder(BiTreeNode *t, void (*Visit)(DataType item))
/*Pre order traversal binary tree t. For the sake of generality, the access operation is designed as a part of the binary tree traversal function
 Function virtual arguments (* Visit)() */
{ if (t ! =NULL) {
Visit(t->data); //visit
PreOrder(t->leftChild, Visit);
PreOrder(t->rightChild, Visit); }
}
//Time complexity O(n)

② Medium order traversal

It is similar to the traversal of binary tree

③ Postorder traversal

It is similar to the traversal of binary tree

2. Breadth first traversal

Hierarchical traversal (also known as breadth first traversal)

Starting from the root node, proceed from top to bottom and from left to right
Row traversal.

Since the next node of the first visited node will be accessed first,
Therefore, a queue is used to store the root node address of the subtree that has not been processed
(1) Initialize queue
(2) Put the root node pointer into the queue
(3) Loop when the queue is not empty

• Out of queue
• Access the original team header element;
• Put the left child pointer of the original team header element into the queue;
• Put the right child pointer of the original team header element into the queue;