1. Sequential search
Sequential search is the basic search algorithm for traversing and comparing the array / linked list according to the original sequence.
1.1 algorithm implementation
- Start with the last data element in the table and compare with the key of the record one by one
- If the matching is successful, the search is successful; Conversely, if there is no successful match until the first keyword in the table is searched, the search fails.
- Time complexity: O(n)
Static lookup tables can be represented by either sequential tables or linked list structures. Although one is an array and one is a linked list, they are basically the same when doing lookup operations. Here we use arrays for operations.
// Sequential search -- if found, return the found value; otherwise, return 0
int SequentialSearch(int arr[], int len, int KeyData)
{
// The first method: consider whether to cross the boundary every cycle
// int tmp = 0;
// for (int i = 0; i < len; i++) {
// if (arr[i] == KeyData)
// return i;
// }
//The second method is optimization
int i;
arr[0] = KeyData; //Set arr[0] as the keyword value, also known as "sentry"
i = len - 1; // Start of loop array tail
while (arr[i] != KeyData) {
i--;
}
return i;
}
1.2 testing
void printf_arr(int arr[],int size) //Print array
{
int i = 0;
for (; i < size; i++) {
printf("%d ", arr[i]);
}
printf ("\n");
}
int main()
{
int arr[] = {90, 70, 34, 35, 26, 89, 56};
int len = sizeof (arr) / sizeof (arr[0]);
printf ("Original data:\n");
printf_arr (arr, len);
int retData = SequentialSearch(arr, len, arr[6]);
printf("Array found[%d] Data is: %d\n", retData, arr[6]);
return 0;
}

2. Binary Search
Binary search, also known as half search, is a search algorithm to find a specific element in an ordered array. We can know from the definition that the premise of using binary search is that the array must be orderly. It should be noted that our input is not necessarily an array, but also the starting position and ending position of an interval in the array.
- Sequential storage structure must be adopted.
- Must be ordered by keyword size.
- Time complexity: O( l o g n log_{n} logn)
2.1 algorithm implementation

int binary_search(int key,int a[],int n)
{
int left, right, mid;
int count = 0,count1=0;
left = 0;
right = n-1;
while(left < right) { //Execute loop body statement when the search range is not 0
count++; //count record search times
mid=(left + right) / 2; //Find the middle position
printf ("The first %d Search times, left : %d right : %d mid : %d\n", count, left, right, mid);
if(key < a[mid]) //When key is less than the middle value
right = mid - 1; //Determine the left sub table range
else if(key > a[mid]) //When the key is greater than the intermediate value
left = mid + 1; //Determine the right sub table range
else if(key == a[mid]) { //When the key is equal to the intermediate value, the search is successful
printf("\n Search succeeded!\n\n lookup %d second!", count); //Output the number of searches and the position of the searched element in the array
count1++; //count1 records the number of successful searches
break;
}
}
if(count1 == 0) //Determine whether the search failed
printf("Search failed!"); //Search failed, output no found
return mid;
}
2.2 testing
void printf_arr(int arr[],int size) //Print array
{
int i = 0;
for (; i < size; i++) {
printf("%d ", arr[i]);
}
printf ("\n");
}
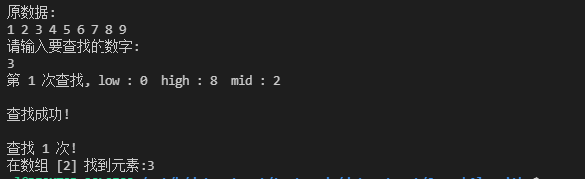
int main (void)
{
int i, key, a[100], n;
printf("Please enter the length of the array:\n");
scanf("%d",&n); //Enter the number of array elements
printf("Please enter an array element:\n");
for(i = 0; i < n; i++)
scanf("%d",&a[i]); //Enter an ordered sequence of numbers into array a
printf ("\n Original data:\n");
printf_arr (a, n);
printf("\n Please enter the element you want to find:\n");
scanf("%d",&key); //Enter the keyword you want to find
int pos = binary_search(key, a, n);
if(pos != -1)
printf("\n In array [%d] Find element:%d\n", pos, key);
else
printf("\n Element not found in array: %d\n", key);
return 0;
}
3. Interpolation Search
- Interpolation search is a search method of ordered table.
- Interpolation search is a search method based on the comparison between the search keyword and the maximum and minimum record keyword in the search table.
- Interpolation search is based on binary search, and the selection of search points is improved to adaptive selection to improve the search efficiency.
- For the lookup table with large table length and uniform keyword distribution, the average performance of interpolation lookup algorithm is much better than half lookup. On the contrary, if the distribution in the array is very uneven, interpolation search may not be a very appropriate choice.
- Complexity analysis: the time complexity of finding success or failure is O( l o g 2 log_{2} log2( l o g n log_{n} logn)).
3.1 algorithm implementation
Half search this search method is not adaptive (that is, it is a fool). The search points in binary search are calculated as follows: mid = (low + high) / 2, that is, mid = low + 1/2 * (high - low); By analogy, we can improve the search points as follows:
mid = ((key - a[low]) * (high - low )) / (a[high] - a[low]) + low
That is, 1 / 2 of the above proportional parameter is improved to be adaptive. According to the position of the keyword in the whole ordered table, the change of mid value is closer to the keyword key, which indirectly reduces the number of comparisons.
int Interpolation_search(int *a, int key, int n) //Interpolation lookup
{
int mid, low, high;
int count = 0,count1=0;
low = 0,high = n - 1;
while(low <= high){
count++;
mid = ((key - a[low]) * (high - low )) / (a[high] - a[low]) + low;
printf ("The first %d Search times, low : %d high : %d mid : %d\n", count, low, high, mid);
if(a[mid] < key) {
low = mid + 1;
} else if (a[mid] == key) {
printf("\n Search succeeded!\n\n lookup %d second!",count); //Output the number of searches and the position of the searched element in the array
count1++;
break;
} else {
high = mid - 1;
}
}
if(count1 == 0) //Determine whether the search failed
printf("Search failed!"); //Search failed, output no found
return mid;
}
3.2 testing
void printf_arr(int arr[],int size) //Print array
{
int i = 0;
for (; i < size; i++) {
printf("%d ", arr[i]);
}
printf ("\n");
}
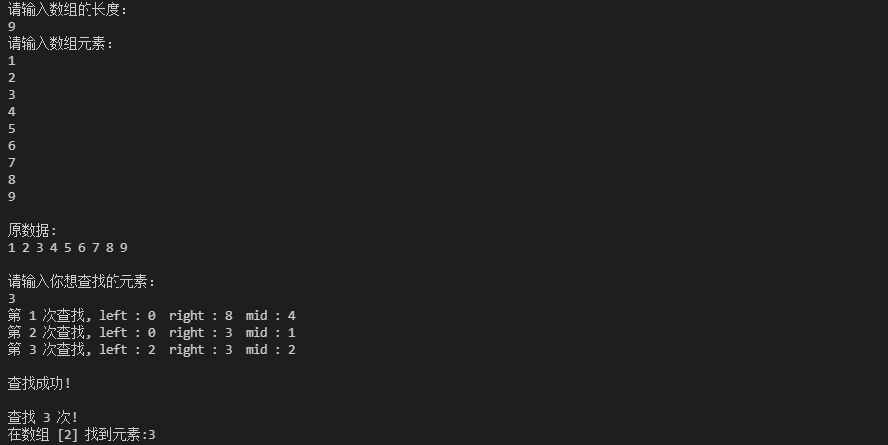
int main()
{
int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int n = sizeof (arr) / sizeof (arr[0]);
int key;
printf ("\n Original data:\n");
printf_arr (arr, n);
printf("Please enter the number you want to find:\n");
scanf("%d",&key);
int pos = Interpolation_search(arr, key, n);
if(pos != -1)
printf("\n In array [%d] Find element:%d\n", pos, key);
else
printf("\n Element not found in array: %d\n", key);
return 0;
}
4. Fibonacci Search
- The golden ratio, also known as the golden section, refers to a certain mathematical proportional relationship between the parts of things, that is, the whole is divided into two. The ratio of the larger part to the smaller part is equal to the ratio of the whole to the larger part, and its ratio is about 1:0.618 or 1.618:1.
- It is also an improvement algorithm of binary search. By using the concept of golden ratio, select the search point in the sequence to search and improve the search efficiency. Similarly, Fibonacci search is also an ordered search algorithm.
- Time complexity: l o g 2 n log_2{n} log2n
4.1 algorithm implementation
Compared with the half search, the key value to be compared is generally compared with the element at mid = (low+high) / 2. The comparison results are divided into three cases:
-
Equal, the element at the mid position is the desired value
-
Greater than, low = mid + 1;
-
Less than, high = mid - 1.
Fibonacci search is very similar to half search. It divides the ordered table according to the characteristics of Fibonacci sequence. He asked that the number recorded in the start table be 1 less than a Fibonacci number, and n=F(k)-1;
Start to compare the K value with the record at position F(k-1) (and mid = low + F(k-1)-1), and the comparison results are also divided into three types
- Equal, the element at the mid position is the desired value
- Greater than, low=mid+1,k-=2;
Note: low=mid+1 indicates that the element to be searched is in the range of [mid+1,high], k-=2 indicates that the number of elements in the range of [mid+1,high] is n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1, so Fibonacci search can be applied recursively. - Less than, high=mid-1,k-=1.
Note: low=mid+1 indicates that the element to be searched is in the range of [low,mid-1], k-=1 indicates that the number of elements in the range of [low,mid-1] is F(k-1)-1, so Fibonacci search can be applied recursively.
Core points:
- Fibonacci is a special segmentation method, which is essentially the same as bisection and interpolation;
- Taking advantage of the special properties of Fibonacci sequence, as long as a length can be divided into golden sections, the segmented fragments can still continue the golden section and cycle.
First, we construct a complete Fibonacci sequence, and then start to divide. If it is less than, take the division on the left, and f becomes F-1; If it is greater than, take the division on the right, and f becomes F-2.
#define MAXN 11
/*
*Produce Fibonacci sequence
* */
void Fibonacci(int *f)
{
int i;
f[0] = 1;
f[1] = 1;
for (i = 2; i < MAXN; ++i)
f[i] = f[i - 2] + f[i - 1];
}
int Fibonacci_Search(int *a, int key, int n) //fibonacci search
{
int i, low = 0, high = n - 1;
int mid = 0;
int k = 0;
int F[MAXN];
int count = 0, count1 = 0;
Fibonacci(F);
while (n > F[k] - 1) //Calculate the sequence of n in Fibonacci
++k;
for (i = n; i < F[k] - 1; ++i) //Complete the array
a[i] = a[high];
while (low <= high) {
count++;
mid = low + F[k - 1] - 1; //Golden section according to Fibonacci sequence
printf ("The first %d Search times, low : %d high : %d mid : %d\n", count, low, high, mid);
if (a[mid] > key) {
high = mid - 1;
k = k - 1;
} else if (a[mid] < key) {
low = mid + 1;
k = k - 2;
} else {
if (mid <= high) { //If true, the corresponding position is found
printf("\n Search succeeded!\n\n lookup %d second!",count);
count1++;
break;
} else {
mid = -1;
break;
}
}
}
if(count1 == 0) { //Determine whether the search failed
printf("Search failed!"); //Search failed, output no found
mid = -1;
}
return mid;
}
4.2 testing
void printf_arr(int arr[],int size) //Print array
{
int i = 0;
for (; i < size; i++) {
printf("%d ", arr[i]);
}
printf ("\n");
}
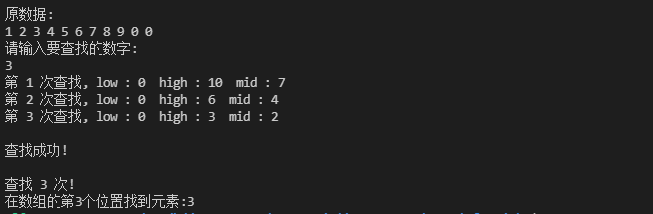
int main()
{
int a[MAXN] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int k, res = 0;
int n = sizeof (a) / sizeof (a[0]);
printf ("\n Original data:\n");
printf_arr (a, n);
printf("Please enter the number you want to find:\n");
scanf("%d", &k);
res = Fibonacci_Search(a, k, n);
if (res != -1)
printf("\n At the end of the array%d Element found at:%d\n", res + 1, k);
else
printf("\n Element not found in array:%d\n", k);
return 0;
}
5. Block search
- Block search, also known as index sequential search, is an improved method of half search and sequential search
- As long as the index table is ordered, block lookup has no sorting requirements for the nodes in the block, so it is especially suitable for the dynamic change of nodes.
5.1 algorithm implementation
Divide n data elements into M blocks (m ≤ n). The nodes in each block do not have to be ordered, but the blocks must be "ordered by block"; That is, the keyword of any element in block 1 must be less than the keyword of any element in block 2; Any element in block 2 must be smaller than any element in block 3
In addition to the lookup table itself, the implementation of the algorithm also needs to establish an index table according to the lookup table.
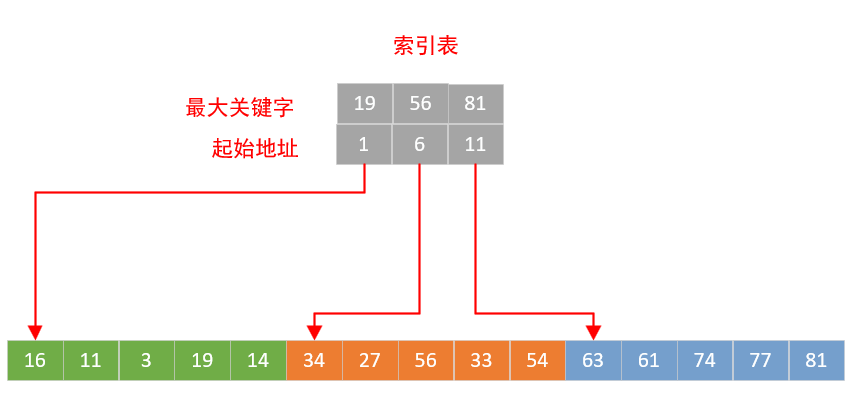
It mainly includes two parts:
- The largest keyword in the sub table section
- Position of the first keyword in the summary table
The index table needs to be sorted in ascending order according to keywords. The lookup table is either ordered as a whole or in blocks.
Block order means that all keywords in the second sub table should be greater than the maximum keyword in the first sub table, all keywords in the third sub table should be greater than the maximum keyword in the second sub table, and so on.
struct index { //Define the structure of the block
int key;
int start;
} newIndex[3]; //Define structure array
int search (int key, int a[]);
int cmp(const void *a, const void* b)
{
return (*(struct index*)a).key>(*(struct index*)b).key ? 1 : -1;
}
int BlockSearch(int key, int a[])
{
int i, startValue;
i = 0;
while (i < 3 && key > newIndex[i].key) { //Determine which block is in, traverse each block, and determine which block the key is in
i++;
}
if (i >= 3) { //If it is greater than the number of blocks, 0 is returned
return -1;
}
startValue = newIndex[i].start; //startValue is equal to the starting value of the block range
while (startValue <= startValue + 5 && a[startValue] != key) {
startValue++;
}
if (startValue > startValue + 5) { //If it is greater than the end value of the block range, there is no number to find
return -1;
}
return startValue;
}
5.2 testing
int main()
{
int i, j=-1, k, key;
int a[] = {16, 11, 3, 19, 14, 34, 27, 56, 33, 54, 63, 61, 74, 77, 81};
//Confirm the starting and maximum values of the module
for (i=0; i<3; i++) {
newIndex[i].start = j+1; //Determines the starting value of each block range
j += 6;
for (int k=newIndex[i].start; k<=j; k++) {
if (newIndex[i].key<a[k]) {
newIndex[i].key=a[k];
}
}
}
//Sort the structure according to the key value
qsort(newIndex,3, sizeof(newIndex[0]), cmp);
//Enter the number to query and call the function to find
printf("Please enter the number you want to find:\n");
scanf("%d", &key);
k = BlockSearch(key, a);
//Output search results
if (k>0) {
printf("Search succeeded! The position of the number you are looking for in the array is:%d\n",k+1);
} else {
printf("Search failed! The number you are looking for is not in the array.\n");
}
return 0;
}

6. Tree table search
The simplest tree table lookup algorithm -- binary tree lookup algorithm
Reference link: Nonlinear structure -- simple tree correlation
7. Hash Search
Hash lookup is a method of searching by calculating the storage address of data elements.
The steps to implement hash lookup are as follows:
- Construct a hash table with a given hash function;
- Resolve the address conflict according to the selected conflict handling method;
- Perform a hash lookup based on the hash table.
7.1 hash table
Hash table (also known as hash table) is a data structure that is accessed directly according to the key value. That is, it accesses records by mapping key values to a location in the table to speed up the search. This mapping function is called a hash function, and the array of records is called a hash table.
In short, the establishment of a hash table is similar to a mathematical function. Replace the key in the function with the keyword used to find the record, and then bring the value of the keyword into a carefully designed formula to find a value that represents the hash address stored in the record.
Hash address = f (key)
The hash address only represents the storage location in the lookup table, not the actual physical storage location. f () is a function that can quickly find the hash address of the data corresponding to the keyword, which is called "hash function".
7.1.1 construction of hash table
7.1.1.1 direct addressing method
Hash address: f(key) = a * key + b (a,b are constants)
- Advantages: simple, uniform and conflict free.
- Application scenario: you need to know the distribution of keywords in advance, which is suitable for small and continuous lookup tables
7.1.1.2 digital analysis method
Is to analyze our keywords, take one of them, or displace it, overlay it, and use it as an address. For example, the first six digits of our student number are the same, but the last three digits are different. We can use the student number as the key and the last three digits as our hash address. If we are still prone to conflict, we can process the extracted numbers again. Our purpose is only one. We provide a hash function to reasonably allocate keywords to each position of the Hash list.
In the selection method, try to select bits with more changes to avoid conflicts.
- Advantages: simple, uniform, suitable for the case of large number of keywords
- Application scenario: the number of keywords is large, the distribution of keywords is known, and several bits of keywords are uniform
7.1.1.3 folding method
Process our keywords and then use them as our hash address. The main idea is to divide the keywords into parts with equal digits from left to right, then overlay and sum them, and take the last few digits as the hash address according to the length of the hash table.
For example, if our keyword is 123456789, we divide it into three parts, 123456789, and then add it to 1368, and then we take the next three digits 368 as our hash address.
-
Advantages: you don't need to know the keyword in advance
-
Application scenario: it is suitable for the situation with a large number of keywords
7.1.1.4 division and remainder method
Hash address: F (key) = key% P (P < = m) m is the length of the hash table.
- Advantages: high calculation efficiency and flexibility
- Application scenario: do not know keyword distribution
7.1.1.5 multiplication hash method
- Multiply the constant a (0 < a < 1) by the keyword k and extract the fractional part of k A
- Multiply m by this value and round it down
Hash address: F (k) = floor (m * (KA% 1))
Ka% 1 means taking the decimal part of keyA
- Advantages: the selection of m is not particularly critical. Generally, it is a power of 2 (m = 2 ^ P, P is an integer)
- Application scenario: do not know keywords
7.1.1.6 square middle method
This method is relatively simple. Suppose the keyword is 321, then its square is 103041, and then extract the middle three bits, 030 or 304, as the hash address. For example, if the keyword is 1234, its square is 1522756, and the middle three bits are 227 for hash address
- Advantages: flexible and wide range of application
- Applicable scenario: the keyword distribution is unknown and the number of digits is not very large.
7.1.1.7 random number method
Hash address: f(key) = random(key)
Here, random is a random function. When the length of key s is different, this method is more appropriate.
- Applicable scenario: when the length of keywords is different
7.1.2 methods for handling hash conflicts
Corresponding to different keywords, you may get the same hash address, that is, key1 ≠ key2, but f(key1)=f(key2). This phenomenon is conflict, and this conflict can only be reduced as much as possible and can not be completely avoided. Because the hash function is an image from the keyword set and address set, the keyword set is usually large, and the elements of the address set are only the address values in the hash table.
7.1.2.1 open address method
The open address method is to find the next empty hash address in case of conflict. As long as the list is large enough, the empty hash address can always be found and the record is stored. In order to insert an element using the open address method, it is necessary to continuously check the Hash list, or probe.
Open addressing method H (key) = (H (key) + d) MOD m (where m is the table length of the hash table and d is an increment). When the obtained hash address conflicts, select one of the following three methods to obtain the value of d, and then continue the calculation until the calculated hash address is not in conflict. The three methods are:
Linear detection method: d=1, 2, 3,..., m-1
Secondary detection method: d=12, - 12, 22, - 22, 32
Pseudo random number detection method: d = pseudo random number
7.1.2.2 rehashifa
Use different hash functions to obtain another hash address until there is no conflict.
f,(key) = RH,( key ) (i = 1,2,3,4......k)
7.1.2.3 chain address method
When the key is different and f(key) is the same, we store these synonyms in a single linked table, which is called the synonym sub table, and only the header pointer of the synonym sub table is stored in the hash table. We still use the example just now. The keyword set is {12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 21}, and the table length is 12. We use the hash function f(key) = key mod 12. After we use the chain address method, there will be no conflicts. No matter how many conflicts there are, we just need to add nodes to the synonym sub table.
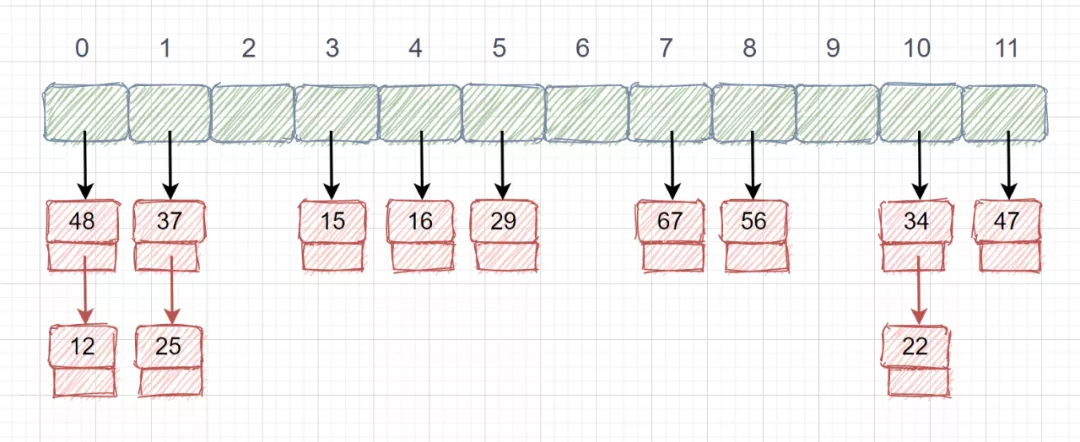
7.1.2.4 public spillover area method
When creating a hash table, another table is created at the same time to store all records with hash conflicts in the overflow table.
7.2 algorithm implementation
define HASHSIZE 7 //Defines the length of the hash table as the length of the array
#define NULLKEY -1
typedef struct{
int *elem;//Data element storage address, dynamic allocation array
int count; //Number of current data elements
}HashTable;
//Initialize hash table
void Init(HashTable *hashTable)
{
int i;
hashTable->elem = (int *)malloc(HASHSIZE*sizeof(int));
hashTable->count = HASHSIZE;
for (i = 0; i < HASHSIZE; i++) {
hashTable->elem[i] = NULLKEY;
}
}
//Hash function (divide and remainder method)
int Hash(int data)
{
return data % HASHSIZE;
}
//Hash table insertion function, which can be used to construct hash table
void Insert(HashTable *hashTable, int data)
{
int hashAddress = Hash (data); //Hash address
//Conflict
while(hashTable->elem[hashAddress] != NULLKEY){
//Conflict resolution using open addressing
hashAddress = (++hashAddress) % HASHSIZE;
}
hashTable->elem[hashAddress] = data;
}
//Hash table lookup algorithm
int Search(HashTable *hashTable, int data)
{
int hashAddress = Hash(data); //Hash address
while(hashTable->elem[hashAddress] != data) {//Conflict
//Conflict resolution using open addressing
hashAddress = (++hashAddress) % HASHSIZE;
//If the data in the found address is NULL or returns to the original position after a circle of traversal, the search fails
if (hashTable->elem[hashAddress] == NULLKEY || hashAddress == Hash(data)){
return -1;
}
}
return hashAddress;
}
test
int main(void)
{
int i,result;
HashTable hashTable;
int arr[HASHSIZE]={13,29,27,28,26,30,38};
//Initialize hash table
Init(&hashTable);
//Constructing hash table by inserting function
for (i = 0; i < HASHSIZE; i++) {
Insert(&hashTable, arr[i]);
}
//Call lookup algorithm
result = Search(&hashTable, 29);
if (result==-1)
printf("Search failed");
else
printf("29 The position in the hash table is: %d\n",result+1);
return 0;
}
