Statement: due to the limited level of the author, this article will inevitably have errors and inaccuracies. I also want to know these errors. I sincerely hope the readers can criticize and correct them.
[contact information] 1583598623@qq.com
[update record] April 19, 2021 (first update)
[Corrigendum record] none
1. What is function recursion?
The programming technique of program calling itself is called recursion. (the core is to make big things small)
Two necessary conditions for recursion:
*There is a constraint. When this constraint is met, recursion will not continue.
*After each recursive call, it gets closer and closer to this limit.
Example: according to the following recursive function: call the function Fun(2), what is the return value
int Fun(int n)
{
if(n==5)
return 2;
else
return 2*Fun(n+1);
}
analysis:
Fun(2)--->Return 16
return 2*Fun(3) 2*8=16
|__Fun(3):8
return 2*Fun(4) 2*4=8
|__Fun(4):4
return 2*Fun(5) 2*2=4
|__Fun(5):2
return 2
Example: print a number in sequence
void print(unsigned int n)//123
{
if (n > 9)
{
print(n / 10);
}
//Else remember that this else cannot be added, not an either or relationship!!!
printf("%d ", n % 10);
}
int main()
{
unsigned int num = 0;
scanf("%u", &num);//123
//Recursion - function calls themselves
print(num);//Each bit of the parameter print of the function can be printed
return 0;
}
Analytical diagram:
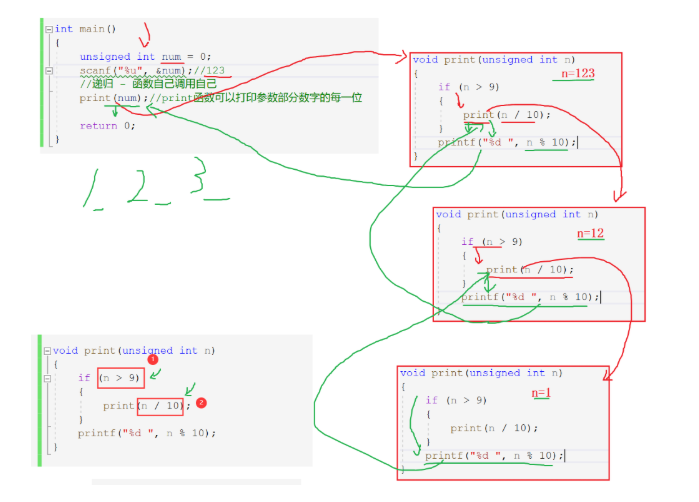
Resolution:
Taking input 123 as an example, we first enter print(123 / 10); Then enter print(12/ 10); Then enter print(1 / 10); Because 1 < 9, 1% 10 = 1, output 1 first, then output 2 to 12% 10 = 2, and then output 3 to 123% 10 = 3 in the outer layer.
2. Recursive overflow
Example:
void test(int n)
{
if (n < 10000)//Deep recursion can easily lead to stack overflow
{
test(n + 1);
}
}
int main()
{
int a = 10;
test(1);
return 0;
}

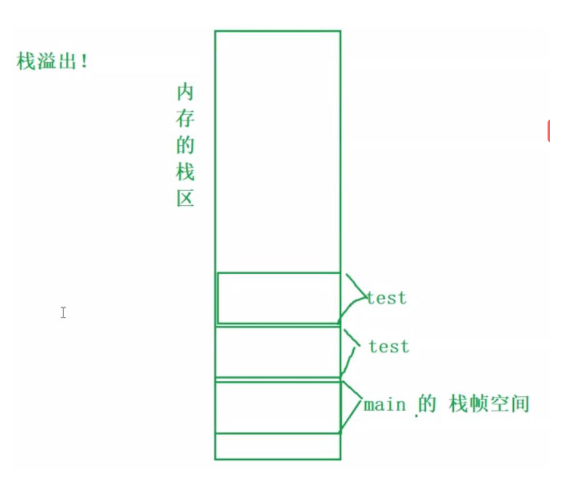
Deep recursion leads to stack overflow!!!
3. (practice several times and focus on understanding): it is not allowed to create temporary variables when writing functions. Find the length of the string.
#include <string.h>
//1. Non recursive solution
int my_strlen(char* str)
{
int count = 0;
while (*str != '\0')
{
count++;
str++;
}
return count;
}
//2. Recursive solution
int my_strlen(char* str)//str is just an address, so * dereference operator is also required
{
if (*str != '\0')
return 1 + my_strlen(str + 1);
//It is wrong to change to + + str or str + +, because the recursion passed in does not meet the requirements
else
return 0;
}
int main()
{
char arr[] = "bit";
//['b']['i']['t']['\0']
//
//Simulate the implementation of a strlen function
printf("%d\n", my_strlen(arr));//The array name corresponds to the address of the first element
return 0;
}
Analytical diagram:
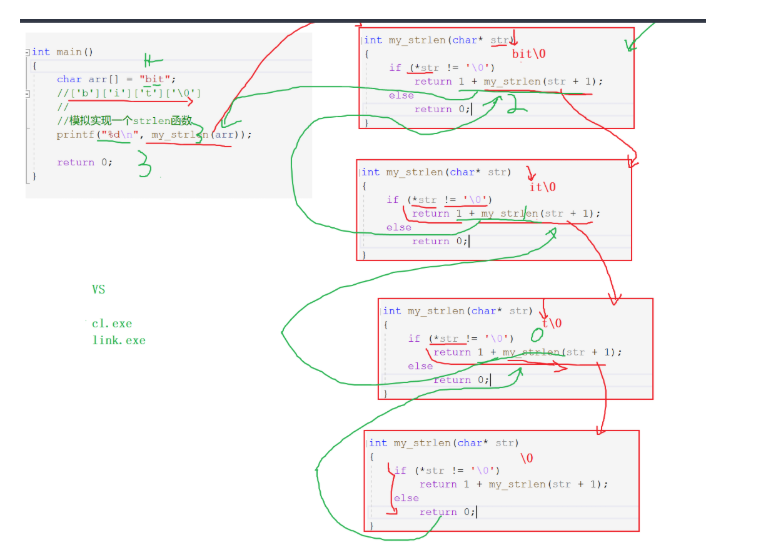
4. Recursion and iteration
Example 1: find the factorial of n
//1. Iteration
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int ret = 1;
for (i = 1; i <= n; i++)
{
ret = ret * i;
}
printf("%d\n", ret);
return 0;
}
//2. Recursion
int Fac(int n)
{
if (n <= 1)
return 1;
else
return n * Fac(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fac(n);
printf("%d\n", ret);
return 0;
}
//There are some functions: it can be implemented iteratively or recursively
Example 2: find the nth Fibonacci number 0, 1, 1, 2, 3, 5, 8, 13, 21 and 34
//Recursion can be solved, but the efficiency is too low and the calculation has been repeated
//Solution 1, recursive efficiency is very low
int count = 0;
int Fib(int n)
{
//Count the number of computers for the third Fibonacci number
if (n == 3)
count++;
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
printf("count = %d\n", count);
return 0;
}
//Solution 2, iterative cycle
int Fib(int n)
{
int a = 1;
int b = 1;
int c = 1;
while (n>2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}
5. Hanoi Tower problem (assuming 24 plates)
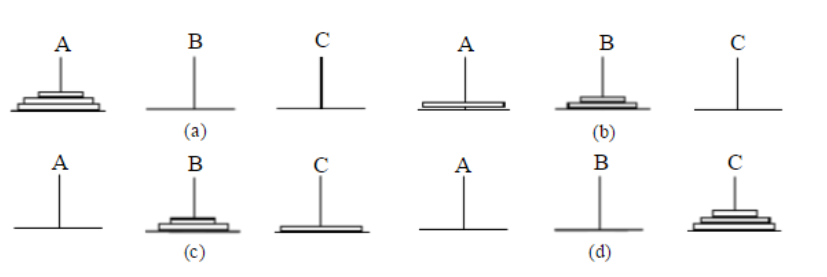
Except for the bottom plate of a, the other 23 are moved to b. at this time, move the bottom plate from a to c.
When the largest plate moves from a to c, b is the remaining 23 plates. A is empty. Now the task is to transfer 23 from b to c.
The subproblem is the same as the original problem, but the scale is adjusted 24 - > 23. The method is similar. First move the top 22 plates from b to a, and then move the bottom plate to c.
...
Repeat the recursion until the scale reaches a predetermined value.
6. Frog jumping steps (similar to Fibonacci sequence)
When n=3, there are two possibilities for the frog to jump for the last time. One is to jump one level for the last time, and the other is to jump two levels for the last time. When n > 3, the last jump method is the same.
We abstract the above idea into a mathematical formula, so that f(n) is the total number of jumps of N steps. If you choose to jump 1 step in the last step, only (n-1) steps can jump before, (n-1) steps can jump, and if you jump 2 steps at the last time, only (n-2) steps can jump before, (n-2) steps can jump, Because the frog's last step is to jump either level 1 or level 2, what I just listed is all the jumping methods of the frog, that is, f(n)=f(n-1)+f(n-2)
7. Write a function reverse_string(char * string) (recursive implementation)
Implementation: the characters in the parameter string are arranged in reverse, not printed in reverse order.
**Requirement: * * string operation function in C function library cannot be used.
/*
Non recursive thinking:
Inverse string, the implementation of the loop is very simple
1. Give two pointers, left to the left of the string and right to the last valid character
2. Swap characters at two pointer positions
3. left The pointer moves backward and the right pointer moves forward. As long as the two pointers do not meet, continue 2. After the two pointers meet, the reverse setting ends
*/
void reverse_string(char* arr)
{
char *left = arr;
char *right = arr+strlen(arr)-1;
while(left<right)
{
char tmp = *left;
*left = *right;
*right = tmp;
left++;
right--;
}
}
/*
Recursive method (well understood):
For the string "abcdefg", the general principle of recursive implementation is as follows:
1. Swap a and g,
2. The rest of the source string is inversed recursively. The rest can be regarded as a valid string, and then inversed in a similar way
*/
void reverse_string(char* arr)
{
int len = strlen(arr);
char tmp = *arr;
*arr = *(arr+len-1);
*(arr+len-1) = '\0';
if(strlen(arr+1)>=2)
reverse_string(arr+1);
*(arr+len-1) = tmp;
}
8. Write a recursive function DigitSum(n), enter a non negative integer and return the sum of the numbers that make up it
For example, if you call DigitSum(1729), you should return 1 + 7 + 2 + 9, and its sum is 19
Input: 1729, output: 19
/*
Idea:
n n < 10
DigiSum(n) =
DibiSum(n/10)+n%10 // Sum of first n-1 bits + nth bit
*/
int DigitSum(int n)//1729
{
if(n>9)
return DigitSum(n/10)+n%10;
else
return n;
}
rr+len-1);
*(arr+len-1) = '\0'; if(strlen(arr+1)>=2) reverse_string(arr+1); *(arr+len-1) = tmp;
}
***
***
<br>
### 8. * * write a recursive function DigitSum(n), enter a non negative integer, and return the sum of the numbers that make up it**
For example, call DigitSum(1729),Should return 1+7+2+9,Its sum is 19
Input: 1729, output: 19
```c
/*
Idea:
n n < 10
DigiSum(n) =
DibiSum(n/10)+n%10 // Sum of first n-1 bits + nth bit
*/
int DigitSum(int n)//1729
{
if(n>9)
return DigitSum(n/10)+n%10;
else
return n;
}