1, What is a sort binary tree?

If the nodes of a binary tree are one child larger or empty than itself and the other is smaller or empty than itself, such a binary tree is called a sorted binary tree, that is, BST.
Then there are two situations. One is that the left child is small and the right child is large, and the other is that the left child is large and the right child is small.
As shown in the figure: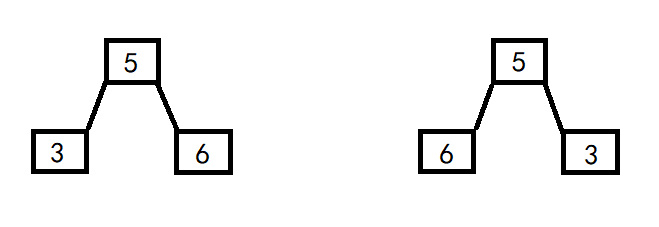
Both cases are OK.
The first case is discussed below and a case is given:

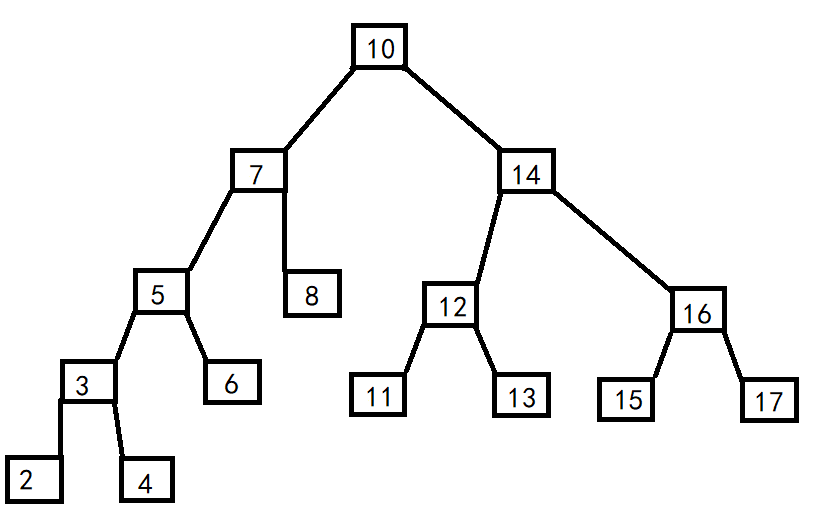
It can be seen that not only the left child of a node is smaller than himself, but also the child of the left child is smaller than himself, and so on.

2, How to create a sort binary tree?

In fact, a binary tree is similar to a two-way linked list in that it stores one data and two addresses. The difference is that a two-way linked list stores its own left node and right node addresses, and a binary tree stores its own two child node addresses. Therefore, it is defined as:

typedef struct Tree{
	int data;
	struct Tree *left;//Left child
	struct Tree *right;//Right child
}*Tree;

To create a tree, first create a node, open up memory, and save the data to data. Because it is still only an independent node, first point to NULL for both left and right.

Tree node;
node = GetNode(10);

Tree GetNode(int data){
	Tree node = (struct Tree *)malloc(sizeof(struct Tree));
	node->data = data;
	node->right = NULL;
	node->left = NULL;
	return node;
}

3, How to insert new nodes according to rules?

The rule is: if you are younger than yourself, you will be my left child, and if you are older than me, you will be my right child. Therefore, you can compare the data before inserting, and then select the insertion position.

Tree newn = GetNode(data[i]);
if(newn->data>node>data)
	node->right = new;
if(newn->data<node>data)
	node->left = new;

However, there are at most three nodes in the binary tree. If 7 and 14 are inserted in turn, as shown in the figure:

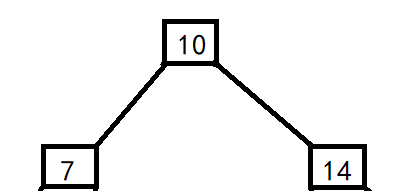
Insert 5 again, judge that it is smaller than 10, insert it to the right, disconnect 7 directly, establish a connection with 5, and will not insert 5 behind 7. Therefore, we should use the idea of recursion to solve this problem.

Tree InsertNode(Tree node,Tree new){
	if(node==NULL)
		return NULL;
	if(new->data<node->data){
		if(InsertNode(node->left,new)==NULL)
			node->left = new;
	}
	if(new->data>node->data){
		if(InsertNode(node->right,new)==NULL)
			node->right = new;
	}
	return node;
}

The insertion should be inserted where there is no node, so the condition for the end of recursion is node==NULL

if(node==NULL)
		return NULL;

If it is not NULL, it indicates that this node exists, then judge the data size. If the new node is larger than this node, insert it to the right child and continue to find it based on the right child. Until a node is found to be empty, it will be the right child of this node; If the new node is smaller than the node, insert it to the left child, and continue to find it based on the left child. Until a node is found to be empty, it will be the left child of the node.
For example, insert 5 on the basis of 10 7 14 nodes
The first call of InsertNode: judged to be empty? Not null, 5 less than 10? Satisfied, continue to look for the left child of 10 as the base point;
The second call of InsertNode: judged to be empty? Not null, 5 less than 7? Satisfied, continue to look for the left child of 7 as the base point;
The third call of InsertNode: it is judged to be empty? NULL, NULL returned;
Return to the second call: return equal to NULL? Satisfied, since you meet the requirements of the left child and you don't have a left child, be your own left child, and then return to node 7.
Return to the second call: return equal to NULL? If not, 10 nodes are returned.

For another example, on the basis of 10 7 14 5 nodes, insert 16
The first call of InsertNode: judged to be empty? Not null, 16 less than 10? Not satisfied, 16 greater than 10? Satisfied, continue to look for the right child of 10 as the base point;
The second call of InsertNode: judged to be empty? Not null, 16 less than 14? Not satisfied, 16 greater than 14? Satisfied, continue to look for the right child of 14 as the base point;
The third call of InsertNode: it is judged to be empty? NULL, NULL returned;
Return to the second call: return equal to NULL? Satisfied, since you meet the requirements of the right child and you don't have a right child, be your right child, and then return to node 14.
Return to the second call: return equal to NULL? If not, 10 nodes are returned*

4, How to traverse a sorted binary tree?

The traversal of binary tree is divided into three types according to the traversal order of root node: first order traversal, middle order traversal and second order traversal. But the overall direction of traversal is the same, that is, from left to right.
First order traversal is: first traverse the root node, and then traverse the left subtree and right subtree.
Middle order traversal is: first traverse the number of left subtrees, and then traverse the root node and right subtree.
Post order traversal is: first traverse the left subtree, and then traverse the right subtree and root node.
① Preorder traversal:

void ShowFirst(Tree node){
	if(node!=NULL){
		printf("%d\t",node->data);
		ShowFirst(node->left);
		ShowFirst(node->right);
	}
}
Take traversal 10 7 14 as an example:

The operation process is as follows:
ShowFirst first first call:
10 nodes equal NULL? Not equal to
First traverse the root node and output data: 10
Then traverse the left subtree and pass in the root node of the left subtree: 7

ShowFirst second call:
7 node equals NULL? Not equal to
First traverse the root node and output data: 7
Then traverse the left subtree and pass in the root node of the left subtree: NULL

ShowFirst third call:
NULL equals NULL? be equal to
End the third call

Return to the second call state:
Start traversing the right subtree and pass in the root node of the right subtree: NULL

ShowFirst fourth call:
NULL node equals NULL? be equal to
End the fourth call
Return to the second call state:
There is no statement. End the second call

Return to the first call state:
Start traversing the right subtree and pass in the root node of the right subtree: 14

ShowFirst fourth call:
14 nodes equal NULL? Not equal to
First traverse the root node and output data: 14
Then traverse the left subtree and pass in the root node of the left subtree: NULL

ShowFirst fifth call:
NULL node equals NULL? be equal to
End the fifth call

Back to the fourth call:
Start traversing the right subtree and pass in the root node of the right subtree: NULL
ShowFirst sixth call:
NULL node equals NULL? be equal to
End sixth call

Return to the second call state:
There is no statement. End the second call

Return to the first call state:
There are no more statements. End.

Final output: 10 7 14

The calling sequence is shown as follows:

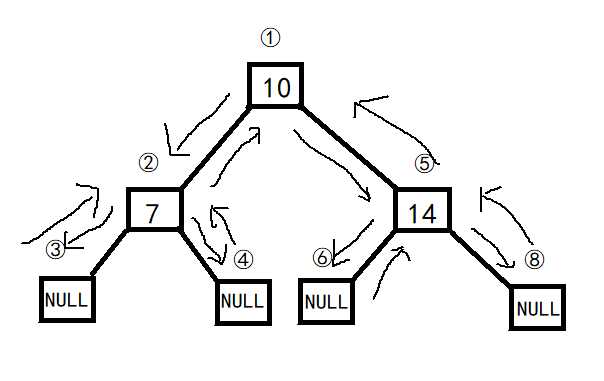
② Medium order traversal

void ShowCent(Tree node){
	if(node!=NULL){
		ShowCent(node->left);
		printf("%d\t",node->data);
		ShowCent(node->right);
	}
}

Instead of describing the execution process in detail, readers can write the operation process by themselves.
The result is: 7 10 14

③ Postorder traversal

void ShowLast(Tree node){
	if(node!=NULL){
		ShowLast(node->left);
		ShowLast(node->right);
		printf("%d\t",node->data);
	}
}

Instead of describing the execution process in detail, readers can write the operation process by themselves.
The result is: 7 14 10
To sum up, recursion and changing the output order.
By analogy, write the following traversal order:

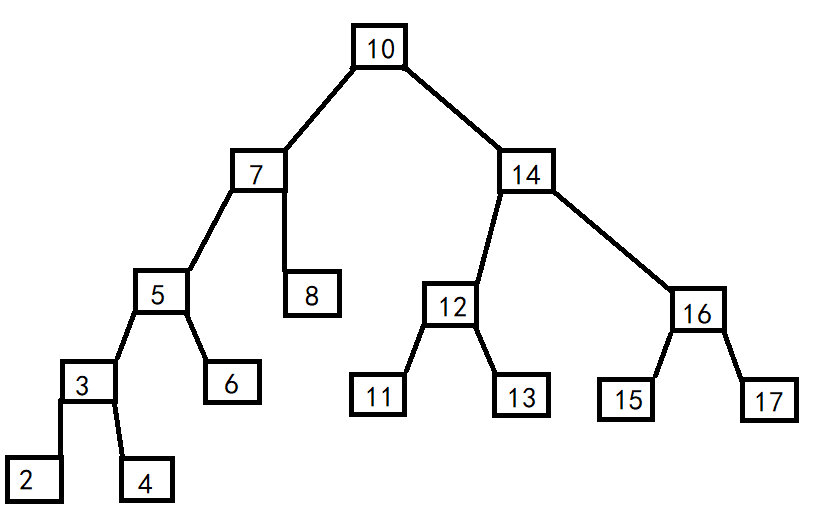
Pre order traversal: 10 7 5 3 2 4 6 8 14 12 11 13 16 15 17
Post sequence traversal: 2 4 3 6 5 8 7 11 13 12 15 17 16 14 10
Middle order traversal: 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17

5, How to delete a node?

In the linked list, to delete a node, you have to change the direction of the front and rear nodes, so that the latter nodes cannot be lost; In a sorted binary tree, if a node is deleted, the parent node of the child node of the node must be changed so that the child cannot be lost. Therefore, if you want to delete the 5 nodes in the figure above, you have to find a node to replace it.
Since the sorting binary tree has rules, then the replaced node must also meet the rules. In this case, that is, the left child of the parent node is smaller or empty than itself, and the right child is larger or empty than itself.
You can't fabricate a node out of thin air. You can only select a node to replace the node to be deleted from the existing node, and then free the node. How can you find the node that meets the conditions?
There are three cases
① The node to be deleted has no children
If there is no child to be taken care of by a trustee, delete it directly and assign it NULL.

② The node to be deleted has only one child
Let the child inherit his position directly. Why?
For example: only left child

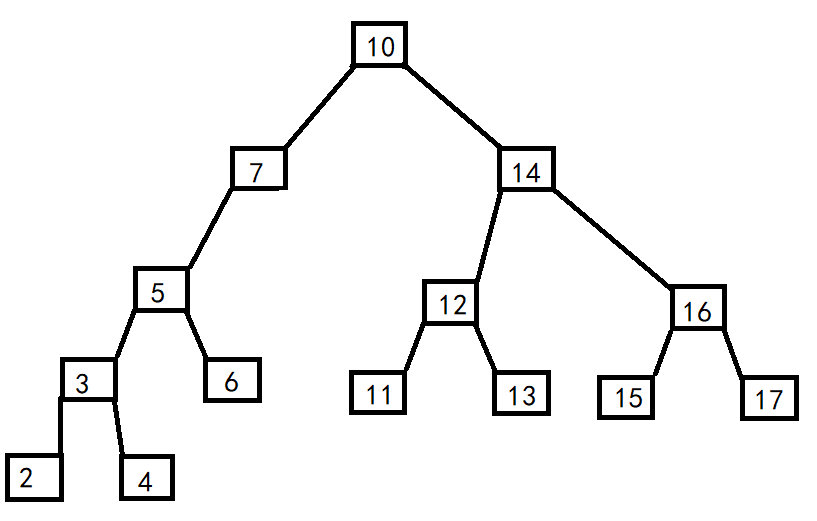
Delete 7 nodes, and the node has only left child 5. Let 5 replace the position of 7 nodes.
analysis:
Less than 5 nodes: since less than 5 nodes meet the requirements, the requirements are also met after changing the position,;
More than 5 nodes: are 5 nodes smaller than 10 nodes? necessary! Because if it is larger than 10, there is no chance to insert it on the left of node 10. It will directly find a suitable position on the right of node 10.

Another example: there is only one right child

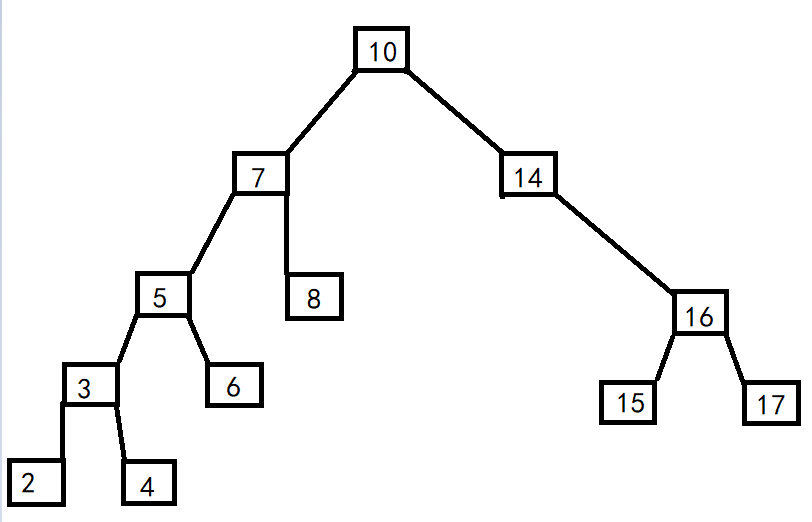
Delete 14 nodes, whose nodes only have the right child 16, and let 16 replace the position of 14 nodes.
analysis:
Below 16 nodes: since below 16 nodes meet the requirements, the requirements are also met after changing the position,;
More than 16 nodes: is 16 nodes larger than 10 nodes? necessary! Because if it is smaller than 10, there is no chance to insert it on the right of 10, and it will directly find a suitable position on the left of node 10.

③ The node to be deleted has two children
There are two ways to find. First, we need to know that for a sorted binary tree, the maximum number is on the far right of the right subtree and the minimum number is on the far left of the left subtree, as shown in the figure, the maximum number is 17 and the minimum number is 2.

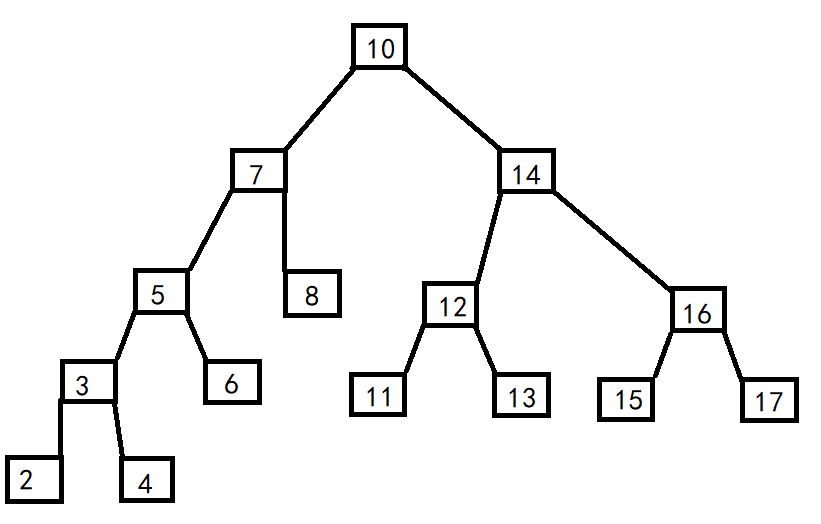
First, find the right child to delete, and then find the leftmost number from the right child, that is, the smallest number in the right subtree, to replace the deleted number.
As shown in the figure above, to delete 14, the right child of 14 is 16, the leftmost number of 16 nodes is 15, replace 14 with 15, and free(15).
Why 15 meet the requirements?
Because 15 is the smallest number in the 14 right subtree (16, 15, 17), but larger than 14, and 14 is larger than the 14 left subtree (12, 11, 13), 15 is also larger than the 14 left subtree. Since the node is larger than the left subtree of the node to be deleted and smaller than the right subtree of the node to be deleted, the condition is exactly met.
Implementation code:

temp = temp->right;
while(temp->left!=NULL){
 	parent = temp;
  temp = temp->left;
 }
 node->data = temp->data;
 free(temp);
 temp = NULL;

Second, find the left child to delete, and then find the rightmost number from the left child, that is, the largest number in the left subtree, to replace the deleted number.
As shown in the figure above, to delete 14, the left child of 14 is 12, the rightmost number of 12 nodes is 13, replace 14 with 13, and free(13).
Why 13 meet the requirements?
Since 13 is the smallest number in the left subtree (11, 12, 13), but smaller than 14, and 14 is smaller than the right subtree (16, 15, 17), 13 is also smaller than the left subtree of 14. Since the node is larger than the left subtree of the node to be deleted and smaller than the right subtree of the node to be deleted, the condition is also satisfied.
The code is similar. It will not be given again with minor changes.

There are two other issues of particular importance:

① How to find the node to delete
Using recursion, if the number of nodes is greater than the number of nodes to be deleted, pass in the right child to continue to find. If the number of nodes is less than the number of nodes to be deleted, pass in the left child to continue to find until it is equal to and start the deletion algorithm.

	if(node==NULL)
		return NULL;
	if(node->data>num)
		node->left = DeleteNode(node->left,num);
	else if(node->data<num){
		node->right = DeleteNode(node->right,num);
	}

② Deleted nodes that should not be deleted
Many bloggers don't consider this problem. If we find an alternative number according to the first method, what should we do for algebra and right children? If an alternative number is found according to the second method, what about the algebra and the left child? If you don't consider it, you can delete the nodes that shouldn't be deleted.
The solution is still recursive. After finding the replacement node and assigning the number of replacement nodes to the number of nodes to be deleted, if the number of replacement nodes still has a right node, continue to delete from the right child (the second method is the left child) of the node to be deleted.

  if(temp->right==NULL){
   	free(temp);
   	temp = NULL;
   }else{
   	node->right  = DeleteNode(node->right,node->data);
   }

6, Complete code

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef struct Tree{
	int data;
	struct Tree *left;
	struct Tree *right;
}*Tree;
Tree GetNode(int data){
	Tree node = (struct Tree *)malloc(sizeof(struct Tree));
	node->data = data;
	node->right = NULL;
	node->left = NULL;
	return node;
}
Tree InsertNode(Tree node,Tree new){
	if(node==NULL)
		return NULL;
	if(new->data<node->data){
		if(InsertNode(node->left,new)==NULL)
			node->left = new;
	}
	if(new->data>node->data){
		if(InsertNode(node->right,new)==NULL)
			node->right = new;
	}
	return node;
}
Tree DeleteNode(Tree node,int num){
	Tree temp;
	if(node==NULL)
		return NULL;
	if(node->data>num)
		node->left = DeleteNode(node->left,num);
	else if(node->data<num){
		node->right = DeleteNode(node->right,num);
	}else{
		temp = node;
		if(temp->right==NULL&&temp->left==NULL){
			free(node);
			node = NULL;
		}else
			if(temp->right==NULL&&temp->left!=NULL){
				node = temp->left;
	        }
		    else
			    if(temp->right!=NULL&&temp->left==NULL){
				    node = temp->right;
				}
			    else{
			    	Tree parent = temp;
			    	int i = 0;//0 means that the next node is the right node
		    		temp = temp->right;
			  	    while(temp->left!=NULL){
			  	    	parent = temp;
			  		    temp = temp->left;
			  		    i = 1;//The next node becomes the left node
			  	    }
			  	    node->data = temp->data;
			  	    if(temp->right==NULL){
			  	    	 temp = NULL;
				  	    if(i==0)
				  	        parent->right = NULL;
				  	    else
				  	    	parent->left = NULL;
			  	    }else{
			  	    	node->right  = DeleteNode(node->right,node->data);
			  	    }
			  	   
			  	   
			    }
	}
	return node;
}
void ShowLast(Tree node){
	if(node!=NULL){
		ShowLast(node->left);
		ShowLast(node->right);
		printf("%d\t",node->data);
	}
}
void ShowFirst(Tree node){
	if(node!=NULL){
		printf("%d\t",node->data);
		ShowFirst(node->left);
		ShowFirst(node->right);
	}
}
void ShowCent(Tree node){
	if(node!=NULL){
		ShowCent(node->left);
		printf("%d\t",node->data);
		ShowCent(node->right);
	}
}
int main(void){
	Tree node;
	int num;
	/*scanf("%d",&num);
	getchar();*/
	node = GetNode(10);
	int data[14] = {7,14,5,8,12,16,3,6,11,13,15,17,2,4};
	int i = 0;
	while(i!=14){
		//if(scanf("%d",&num)==1){
			Tree newn = GetNode(data[i]);
			//getchar();
			InsertNode(node,newn);
			printf("Preorder traversal:");
			ShowFirst(node);
			printf("\n");
			printf("Post order traversal:");
			ShowLast(node);
			printf("\n");
			printf("Middle order traversal:");
			ShowCent(node);
			printf("\n");
		/*}
		else{
			getchar();
		    break;
		}*/
		i++;
	}
	while(1){
		printf("Start deletion:\n");
		if(scanf("%d",&num)==1){
			getchar();
			node = DeleteNode(node,num);
			printf("Preorder traversal:");
			ShowFirst(node);
			printf("\n");
			printf("Post order traversal:");
			ShowLast(node);
			printf("\n");
			printf("Middle order traversal:");
			ShowCent(node);
			printf("\n");
		}
		else
		  break;
	}
	return 0;
}

It was originally entered manually until the end of the input character, but later changed to automatic input. Readers who do not need automatic input can modify the code.
That's it!