inspire

Since it is a non recursive solution, there can be no indirect or indirect reference to itself in the function used. Iteration is to use a complete solution algorithm to bring the number of steps into the algorithm as a parameter for each step to obtain specific results. Therefore, to iterate, we must analyze the law embodied in each step of the moving process of Hanoi tower.

Ideas & some codes

decomposition process

Each step can be broken down into:
1. Decide the disc number to be moved (if n discs are numbered, 1~n from small to large)
Decide where to move the plate.

Therefore, the problem to be solved is:
1. How to determine which plate corresponds to each step;
2. How to determine the current position of the plate and the position to be moved.

Mobile disk number

Assuming that 4 plates are moved, the plates are moved from column 1 to column 3 by default, and column 2 is used as a temporary storage point. The process is as follows (the number in brackets represents the disk number to be moved):

1–2(1)
1–3(2)
2–3(1)
1–2(3)
3–1(1)
3–2(2)
1–2(1)
1–3(4)
2–3(1)
2–1(2)
3–1(1)
2–3(3)
1–2(1)
1–3(2)
2–3(1)

By observing the above formula, we can know:
1. The total number of steps is 15 (i.e. 24 - 1)
2. The steps of moving disk 1 are: [1,3,5,7,9,11,13,15], and the steps of moving disk 2 are [2,6,10,14]; The steps of moving disk 3 are [4,12]; The steps to move disk 4 are [8]
3. Move disk 1 for the first time in step 1; Move disk 2 for the first time in step 2; The first movement of disk 3 is in step 4, and the first movement of disk 4 is in step 8.

Number of intervals

It can be seen from this that the number of steps in disk 1 is 2 (3-1,5-3,7-5), the number of intervals in disk 2 is 4 (6-2,10-6,14-10), and the number of intervals in disk 3 is 8 (12-4) Therefore, it is speculated that the number of intervals of each disk is related to its disk number:

Disc number	Number of intervals
1	2=21
2	4=22
3	8=23
4	24=16

and so on.

prove:
By recursively analyzing the process of moving n plates, we can get:
When n=1, move once;
When n=2, move 1 + 1 + 1 = 3 times (the first and last 1 respectively represent the step of moving No. 1);
When n=3, first move 2 disks to the temporary point, then move No. 3, and finally move No. 1 and No. 2 to the end, so: 3 + 1 + 3 = 7 times
When n, set a n a_{n} an is the total number of steps, then a n a_{n} an​=2 a n − 1 + 1 a_{n-1} + 1 an−1​+1
obtain a n = 2 n − 1 a_{n} = 2^{n} -1 an​=2n−1
The diagram is as follows:

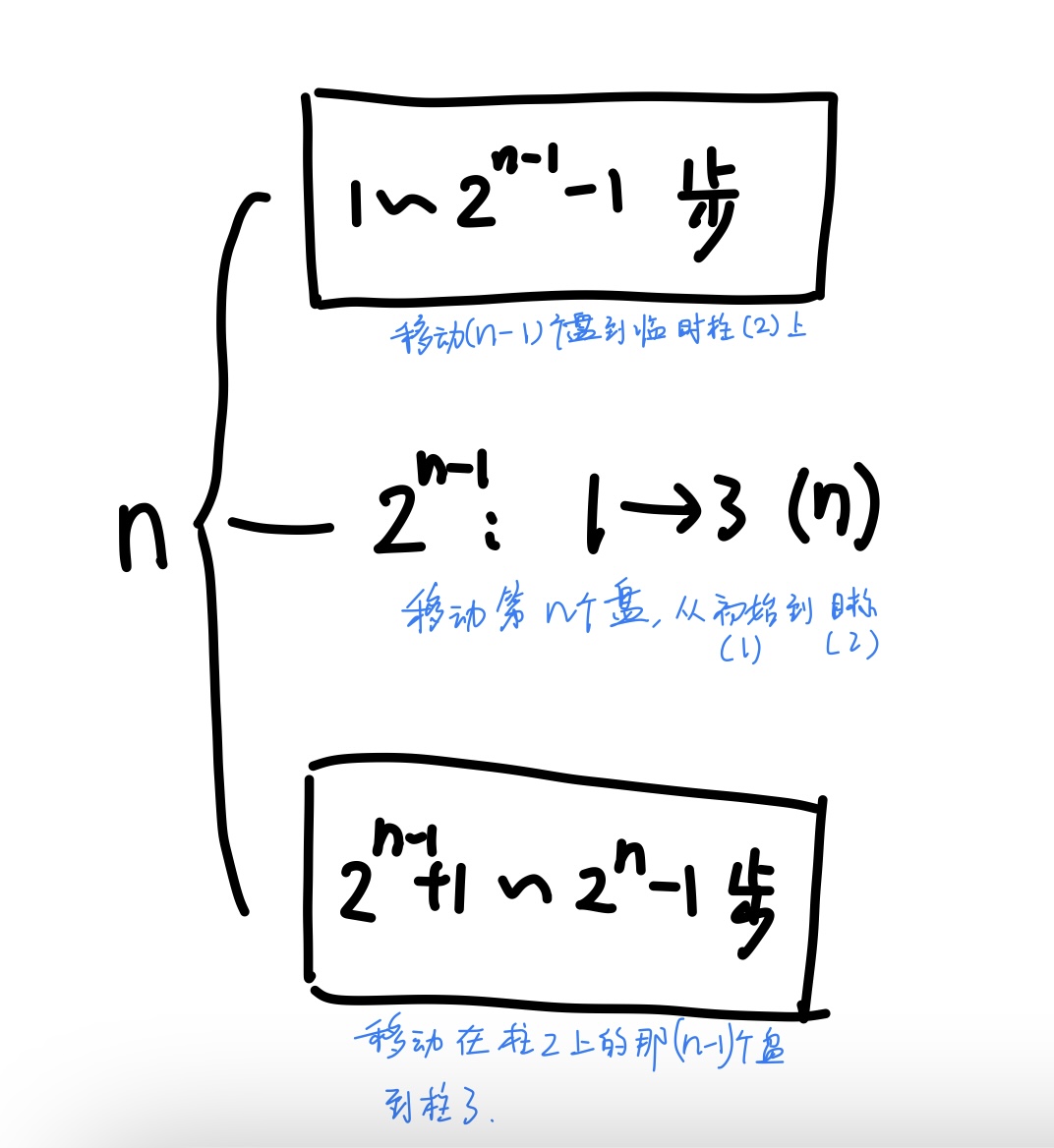
Therefore, mathematical induction can be used to prove the relationship between step interval number and disc number
Set the plates whose total number of moves is n
Including No. 1:
Since it is impossible to move disk 1 in the next step after moving disk 1, the hypothesis of "moving disk 1 in any two consecutive steps" is excluded When the plate with another number (assuming No. a) is moved (at this time, the plates on other columns except No. 1 stay are larger than No. 1), the third step must move No. 1, because before moving, No. A is either larger than No. a, or there is no plate, and it is impossible to move No. a back (invalid operation), so only No. 1 can be moved It is concluded that the step interval of No. 1 is 2
Set the step interval of disk k = 2k
k+1:
The total process is decomposed into (k+1) levels with 2(n-k-1) bifurcations Each fork represents (2k-1 -1) steps to move K plates, so the number of intervals:
a k + 1 = 2 k − 1 + 1 + 2 k − 1 + 1 = 2 k + 1 a_{k+1} = 2^{k}-1+1+2^{k}-1+1 = 2^{k+1} ak+1​=2k−1+1+2k−1+1=2k+1
The + 1 in the middle represents the step of moving disk k+2, and the last + 1 represents the step of moving disk k+1 for the second time

The number of steps corresponding to moving a disk for the first time

According to the above figure, it is very simple to prove this. The step number of moving the nth plate for the first time is 2n-1. Recursively, the step number of moving the nth + 1st plate for the first time is 2n-2. Therefore, the step number of moving the k th plate for the first time is:
2k-1.

Determine the disc number to be moved in a certain step

Now we can solve the first big problem, that is, how to determine the disk number to be moved at each step. According to the above two properties, in step (m), a disk (k) must move (i), that is:
m = 2 k − 1 + ( i − 1 ) ∗ 2 k m = 2^{k-1}+(i-1)*2^{k} m=2k−1+(i−1)∗2k
The high frequency of "2" makes people think of binary (?) It may be possible to use some features of binary to determine (k) inversely by (m).
When i ≠ 0 i \neq 0 When i  = 0, ( i − 1 ) ∗ 2 k (i-1)*2^{k} (i − 1) * 2k must be greater than 2 k − 1 2^{k-1} 2k−1. In other words, the first half of the formula seems to be the lowest part in the binary number. (i) The size of does not affect this fact.
Therefore, in step (m), the lowest digit of 1 in the binary representation corresponding to (m) represents the moving disk number.

Code 1

Complete the functions of this part with an independent function:

#include <iostream>
#Include < ssstream > / / used to convert numbers to strings
#Include < BitSet > / / used to convert numbers to binary form
#include <string>
#include <cmath>


int lowestBit(int num)
{
    //Initialize the stringstream object,
    //bitForm in binary form for storing the number of steps num
    //And bitString in its string form
    stringstream ss;
    bitset<32> bitForm = bitset<32>(num);  //Get the binary form of the number
    string bitString;
    
    //Initialize disk number
    //Considering that the tower of Hanoi may be very high, the unsigned int with a large range is used
    unsigned int position = 0;  
    
    //Convert to string
    ss << bitForm;
    ss >> bitString;
    
	//The for loop determines the position of the first 1 from right to left
	for (unsigned int i = bitString.size(); i >= 0;i--)
    {
        if (bitString[i] == '1')
        {
        	//Note that there is an implicit "\ 0" on the far right of bitString
        	//Therefore, if the first digit is "1", i = 31
            position = bitString.size() - i;
            break;
        }
    }
    return position;
}

Start and end of movement

Looking back at the process of moving four plates, we can also find that:

1–2(1)
1–3(2)
2–3(1)
1–2(3)
3–1(1)
3–2(2)
1–2(1)
1–3(4)
2–3(1)
2–1(2)
3–1(1)
2–3(3)
1–2(1)
1–3(2)
2–3(1)

(1) The route of No. plate is: 1 – 2 -- 3 – 1 -- 2 -- 3 -- 1 – 2 -- 3
(2) The route of plate 1 is: 1 – 3 -- 2 – 1 -- 3
(3) The route of plate 1 is: 1 – 2 -- 3
(4) The route of plate 1 is: 1 – 3
There is a law of "no turning back": (1) will not start from 1-2, and then from the combination of 2-1, 23 and 31. The same is true for the action route of the rest (2, 3 and 4). Because to avoid invalid rounds, when the initial movement of a plate is determined, its trajectory has been determined.
Therefore, there are two kinds of mobile routes:
Sequence: 1 – 2 -- 3 – 1
Reverse order: 1 – 3 -- 2 – 1

Also: the last disk must have only 1 – 3 steps (the default initial is No. 1 and the end is No. 3). According to the upper recursive analysis diagram, the moving track of (3) is opposite to (4), (2) and (3), (1) and (2), and so on.

It is concluded that:
When moving plates with a total number of n, the action track of the k-th plate:
1. Same as n [n-k is an even number]
2. Opposite to n [n-k is odd]

Then we just need to determine the trajectory of each plate according to the plate number and the number of times it moves i i i to determine always.

Code 2

The code is divided into two functions, one is used to collect the starting point, ending point and temporary points provided by the user to simulate the track, and the other is to judge the specific movement according to the current number of steps and disc number:

string movement(unsigned int plateNum,unsigned int stepNum,unsigned int position,int ini,int fin,int tem)
{
	//According to the disc number and the number of steps, the number i is deduced by using the relationship of [step, disc number and times] provided above
	//The specific movement is judged by i
	//plateNum -- total number of plates
	//stepNum -- number of steps
	//position -- disk number
	//ini -- starting point
	//fin -- end point
	//tem -- temporary point

	//Initializes the number of moves moveTimes and the string move
    unsigned int moveTimes = 0;
    string move;
    
    //Calculate moveTimes
    moveTimes = stepNum - static_cast<unsigned int>(pow(2, static_cast<double>(position)-1));
    moveTimes /= static_cast<int>(pow(2, static_cast<double>(position)));
    moveTimes += 1;
    
	//Use moveTimes to judge specific actions
	if((plateNum - position)%2 == 0)
    {
        if ((moveTimes % 3) == 1)
            move = movementGenerator(ini,fin);
        else if ((moveTimes % 3) == 2)
            move = movementGenerator(fin,tem);
        else
            move = movementGenerator(tem,ini);
    }
    else
    {
        if ((moveTimes % 3) == 1)
            move = movementGenerator(ini,tem);
        else if ((moveTimes % 3) == 2)
            move = movementGenerator(tem,fin);
        else
            move = movementGenerator(fin,ini);
    }
    return move;
}


string movementGenerator(int start,int end)
{
	//Return the corresponding action track string
	//For example: start point = 1, end point = 2
	//The string "1 -- 2" is returned
    stringstream ss;
    string moveString;
    ss << start;
    ss<<"--";
    ss << end;
    ss >> moveString;
    return moveString;
}

General process and code

Use a total function hanoi set to run the above functions to solve the hanoi Tower problem. The total code is as follows:

//tower of hanoi
//iteration type
#include <iostream>
#include <bitset>
#include <sstream>
#include <string>
#include <cmath>
using namespace std;

void hanoi(unsigned int, int, int, int);
int lowestBit(int);
string movement(unsigned int, unsigned int, unsigned int,int,int,int);
string movementGenerator(int, int);

int main()
{
    unsigned int plateNum = 0;
    int ini = 0;
    int fin = 0;
    int tem = 0;
    cout << "Enter the plate number: ";
    cin >> plateNum;
    cout << "Enter the ini, fin, and tem: ";
    cin >> ini >> fin >> tem;
    hanoi(plateNum, ini, fin, tem);
    
    

}

//return the position of the first "1" from right to left, AKA the plate number
int lowestBit(int num)
{
    stringstream ss;
    bitset<32> bitForm = bitset<32>(num);
    string bitString;
    unsigned int position = 0;
    ss << bitForm;
    ss >> bitString;
    for (unsigned int i = bitString.size(); i >= 0;i--)
    {
        if (bitString[i] == '1')
        {
            position = bitString.size() - i;
            break;
        }
    }
    return position;
}

//return a string including the movement, such as "A--B"
string movement(unsigned int plateNum,unsigned int stepNum,unsigned int position,int ini,int fin,int tem)
{
    unsigned int moveTimes = 0;
    string move;
    moveTimes = stepNum - static_cast<unsigned int>(pow(2, static_cast<double>(position)-1));
    moveTimes /= static_cast<int>(pow(2, static_cast<double>(position)));
    moveTimes += 1;
    if((plateNum - position)%2 == 0)
    {
        if ((moveTimes % 3) == 1)
            move = movementGenerator(ini,fin);
        else if ((moveTimes % 3) == 2)
            move = movementGenerator(fin,tem);
        else
            move = movementGenerator(tem,ini);
    }
    else
    {
        if ((moveTimes % 3) == 1)
            move = movementGenerator(ini,tem);
        else if ((moveTimes % 3) == 2)
            move = movementGenerator(tem,fin);
        else
            move = movementGenerator(fin,ini);
    }
    return move;
}

string movementGenerator(int start,int end)
{
    stringstream ss;
    string moveString;
    ss << start;
    ss<<"--";
    ss << end;
    ss >> moveString;
    return moveString;
}

//Total function hanoi
void hanoi(unsigned int plateNum, int ini, int fin, int tem)
{
    unsigned int position;
    string move;
    for (unsigned int i = 1; i <= pow(2,static_cast<double>(plateNum))-1;i++)
    {
        position = lowestBit(i);
        move = movement(plateNum, i, position,ini,fin,tem);
        cout << move << endl;
    }
}

Postscript

The solution is for reference c + + iterative recursive implementation of Hanoi Tower (five iterative methods meet your needs) . The author initially felt that it was difficult to realize the tower of Hanoi problem only by iterative method, and was amazed at the way of thinking used in this article. In order to learn how to analyze a more complex problem concretely, this thinking process is specially recorded. If you have any questions, welcome to discuss.