[Eager to get the code directly]

(Linear Table (Non-Linked Table) Source Disk Link: https://pan.baidu.com/s/1SbzGBK0Cv3nV3q14yUhDBw  
Extraction code: s51t  

    Chain List Source Disk Link: https://pan.baidu.com/s/1dhd7Lvcd3yhC5nzcVzWTyA  
Extraction Code: zdzn  )

1. What is a linear table

         What is a linear table? First look at Baidu's explanation:

                        

         Linear table is a kind of sequence and its length is an intrinsic property of itself. The first data type that comes to mind when referring to a sequence is an array naturally! So here's how to construct a linear table class that stores an integer array of data types.

2. Construct a Linear Table Class (SeqList)

        To construct a class, you first need to understand what private attributes are needed, which are some of the inherent components of the class. From Baidu's explanation, you can know two essential elements - 1. Sequence 2. Length of linear table

        Here we define the sequence as an integer array - int a[]; the length is int length;

        Linear tables are limited in length, so it is best to have a limited control over the sequence they store, so define the maximum length of the array as follows: const int MaxSize = 100;

        So there's a rudiment of a class:

#include <iostream>
#include <cstdlib>
#include <string>

using namespace std;
const int MaxSize = 100;

class SeqList
{

private:
    int data[MaxSize];
    int length;

};


int main()
{


}

      Now you should start thinking about what you want a linear table to do

Construction of Linear Tables

      First of all, it is certain that the implementation can construct a linear table, and the construction of a linear table requires its sequence and length, that is, the construction with parameters. In other words, the natural result of a construction without parameters is an empty table. It is easy to do before it is difficult to do so. First, write a construction without parameters:

public:
    //Construct without parameters to get an empty table (that is, a table with a length of 0)
    SeqList()
    {
        length = 0;
    };

        Next, to construct a first-hand linear table with parameters, we need two parameters: 1. Sequence 2. Length of a linear table. With these two parameters, we assign the latter directly to length, and the former to data[]. You might wonder why sorting directly to it is impossible. This is actually quite a start, with the foreshadows embedded first!

        Now that you want to sort, you have to face two everlasting challenges - 1. What is the sort method? 2. What is the sorting algorithm?

        For the second question, it is recommended to use the fast sort directly from the algorithm library. For the first question, interaction is required to get the answer. Then we get a new ship property of SeqList, the sort method, which defines a bool-type variable, from small to large if it is false, and vice versa. And we define the default sort order artificially from small to large, when our classes begin to take shape:

#include <iostream>
#include <algorithm>
#include <string>

using namespace std;
const int MaxSize = 100;

class SeqList
{
public:
	//No parameter construct, that is, construct an empty linear table
	SeqList()
	{
		length = 0;
		rev = false;//The default is to hit big from small
	};

	//Construction with parameters, reverse stands for reverse sort order, default from small to large
	SeqList(int a[], int n, bool reverse = false)
	{
		rev = reverse;
		length = n;
		//Quickly arrange the given array
		sort(a, a + n);
		if (!reverse)
		{
			for (int i = 0; i < n; i++)
				data[i] = a[i];
		}
		else//Assign data in reverse order
		{
			for (int i = 0; i < n; i++)
			{
				data[i] = a[n - 1 - i];
			}
		}
	};

private:
	int length;  //Linear Table Length
	int data[MaxSize]; //Data stored in an array
	bool rev; //Judging from small to large or from large to small
};

P.S.: Remove an idea to steal chickens and play with them:

         When constructing with parameters, you might wonder why you have to enter an n to represent the length pinch? Now that I know the array of data, can't I just calculate the length of the array? Since we know that an integer takes up 4 bytes of space, isn't the length of the integer array a[] sizeof(a)/4?

        This gives us a simpler construction with parameters:

pubilc:
    //Construction with parameters, reverse stands for reverse sort order, default from small to large
	SeqList(int a[], bool reverse = false)
	{
		rev = reverse;
		length = sizeof(a)/4;
		//Quickly arrange the given array
		sort(a, a + length);
		if (!reverse)
		{
			for (int i = 0; i < length; i++)
				data[i] = a[i];
		}
		else//Assign data in reverse order
		{
			for (int i = 0; i < length; i++)
			{
				data[i] = a[length - 1 - i];
			}
		}
	};

         This way you will find that the length here is always 1, which I was particularly confused at first, but later I looked for data to know that the array datatype a[] as a parameter in the function degenerates into a pointer, that is, the number of bytes sizeof(a) gets at this point is actually only the number of bytes occupied by a datatype of data!  

        That is, the sizeof(a) in the above function is equivalent to the external sizeof(a[0])=4. So the length will always be 1. This is why an int n parameter is required in a parametric construction.

Judging whether a linear table is empty or not-Getting private attributes

         What other interesting features can you achieve after constructing a linear table? You might be thinking about output, bit insertion, value insertion or something. Before that, there are two basic things to do --- 1. Determine if a linear table is empty 2. Get private attributes

        Just as the so-called "ten thousand feet tall building" rises flat, the foundation is the two construction methods and three private attributes we wrote above. Next we'll get the raw materials for building a house - concrete, stone, and so on. This means whether the linear table is empty or not and externally gets the value of the private property.

        First, let's look at whether it's empty or not. Looking back at the definition of a one-handed empty linear table, a zero-length linear table, we just need to decide if length is zero.

bool empty()
	{
		return (length == 0) ? true : false;
	}

        ok, just write down the function to get the data sequence [], length length, and sort order.

//Get the stored data series
void get_data(int a[])
{
	for (int i = 0; i < length; i++)
		a[i] = data[i];
}
//Get Length
int get_length()
{
	return length;
}
//Get sort order, assuming small to large
bool get_rev()
{
	return rev;
}

Get data information (that is, find function)

        Next, let's implement the one-hand information acquisition function speaker! When it comes to getting data information, as a whitewash, the first thing I think about is getting a data by subscript index, which is getting the value of data[i] by giving I.

        So the opposite? If I want to find out if there is an element x in this linear table, is it the value of I given data[i]? Yes, this is what is called value-by-value lookup, and the other is what is called bit-by-bit lookup.

        So let's first conceive how to write these two functions in one hand, and first deny the overload, because the data type of subscript index or data[i] is int, and then the overload is sent, so we have to be honest.

        Make it simple before you do it. Obviously, bitwise searching is the easiest (probably because it fits most naturally), and direct return data[index] is done.

        But be aware of exception handling: because linear tables are finite (length), you can't let index take its own value, so you can't return data if the index doesn't belong to the [0, length] range, and you should throw an exception.

//Bit Acquisition
int get_index(int index)
{
	if (index<0 || index>length - 1)
	{
		cout << "Given subscript overflow range!" << endl;
		throw 1;
	}
	else
	{
		return data[index];
	}
}

        It then implements a one-hand value-by-value lookup, which returns the subscript index of the x-value in the linear table. Consider the exception first - there is no X in the data. Because I touched py while learning C, I immediately thought of how PYY handled this situation and returned a - 1 representative who could not find it.

         So I defined the index to return as -1 from the start. If I don't find x by traversing the entire data in the for loop, I return i ndex (return -1). If I'm lucky, I traverse, hey, I find it, I rush back and I'm done.

//Get by value
int get_num(int x)
{
	int index = -1;//Return to -1 if not found
	for (int i = 0; i < length; i++)
	{
		if (data[i] == x)
		    return i;
	}
	return index;
}

Show a linear table (the entire contents of the output linear table)

        There's nothing to say about this. To code directly is to output the contents of the table directly.

//Show Linear Table
void show()
{

	cout << "The linear table length is" << length << endl;
	string sort_func = (rev) ? "From large to small" : "From small to large";
	cout << "The linear table is arranged as" << sort_func << endl;
	for (int i = 0; i < length; i++)
	{
		cout << "No." << i + 1 << "Elements are:" << data[i] << endl;
	}

}

Delete element

        As with finding, there are two ways to delete elements --- 1. Bitwise deletion (delete data[i]) 2. Value deletion (delete the first or all data whose value is x)

        Now let's do it one by one. From the bracketed thinking above, we can see that 1 is simpler, so hit Delete Bitwise first:

        Since it's bit-wise, you need to handle the exception of one-hand location overflow (see Bit-wise Lookup for details), so how do you delete the index when it's legal? Think about the changes after and before deletion - all the elements before index have not changed, and all the elements after index have moved forward one, so we can simulate the process of moving forward the following elements and complete the deletion:

        There is another thing!! Length is an inherent property of a linear table. After deleting an element, the length of the linear table will be -1, so remember to write length--!!

//Bitwise deletion of elements
void del_index(int index)
{

    if (index<0 || index>length - 1)
	{
		cout << "Subscript overflow, cannot be deleted!" << endl;
		throw 1;
	}

	for (int i = index; i < length - 1; i++)
	{
		data[i] = data[i + 1];
	}
	length--;//Length-1

}

        Next, write the more cumbersome delete by value:

        Value-by-value deletion can be based on bitwise deletion, which is divided into three steps:

        1. Find it (find all eligible subscripts)

        2. Handle exceptions (errors when it is not found)

        3. Kill him (delete all elements corresponding to the subscript to be deleted)

public:
    //Delete elements by value
	void del_num(int num, bool all = false)
	{

		if (!all)
		{
			int index = get_num(num);

			if (index == -1)
			{
				cout << "Delete failed! There are no elements in the linear table" + to_string(num) << endl;
				throw 1;
			}
			
			del_index(index);

		}
		
		else
		{
			int index = get_num(num);

			if (index == -1)
			{
				cout << "Delete failed! There are no elements in the linear table" + to_string(num) << endl;
				throw 1;
			}

			//Delete all when found
			int ind[MaxSize];//Anti-heavenly is all a number
			int count = 0;
			for (int i = index; i < length; i++)
			{
				if (data[i] == num)
				{
					ind[count] = i;
				}
			}
			//Delete
			for (int i = 0; i <= count; i++)
			{
				del_index(ind[i]-i);
			}

		}

	}

        When dealing with deletion, you can also apply the above three paragraphs, just need to pay attention to one point - deletion, because more than one subscript is to be deleted, so after each subscript is deleted, all the subscripts to be deleted will move forward one space!

        The first element is not offset, and the corresponding subscript in the array of subscripts to be deleted is 0. The second element moves forward by 1 space, with the corresponding subscript 1 in the array of subscripts to be deleted; The third element moves forward 2 spaces, and the corresponding subscript in the array of subscripts to be deleted is 2...

        Get regular! So write the third step as del_index(ind[i]-i) is fine!

Insert (Bitwise and Value Insert)

        OK! And then there's the last function I can think of in a class, which is interpolation ♂ enter

        Since ancient times, insertion has been a topic that people enjoy endlessly (dog heads keep alive), and insertion also has two interpolation methods, bitwise and interpolation. First come to Kangkang bitwise. Generally speaking, bitwise is the simplest haha!

        To achieve bitwise insertion, let's imagine inserting the value x at i, data[i]=x. What happens in the linear table after that? Obviously, easy to get:

1.0~i-1 data not moving

2.i~length-1 data moved one bit backwards

3. length+1 after insertion

        OK! Then we can imitate 2 or 3 steps!

        Note here that in the second step, if you want to insert at the end of the table, i.e. index=length-1, there is no data after that and you can't move back, so this case is handled separately!

public: 
    //Bitwise insertion
	void insert(int num, int index)
	{

		if (index<0 || index>length)
		{
			cout << "Given subscript overflow range!" << endl;
			throw 1;
		}

		else
		{
			if (index != length)
			{
				for (int j = length; j >= index + 1; j--)
					data[j] = data[j - 1];
				data[index] = num;
				length++; //Length after insertion+1
			}
            //Insert at the end of the table, special case
			else
			{
				data[length] = num;
				length++;
			}
			
		}

	}

         With the experience of bitwise insertion, the three-segment insertion by value comes to life:

        1. Find the right location

        2. Not found (throwing an exception)

        3.Insert!

        Recycle Volume: The reason for sorting linear tables all at once is to find values here, because only in an ordered linear table can a suitable insertion position be found for a value!

        Here is the first step to note:

        For example, if data[i] <= num <= data[i+1], where should num be inserted at this time? Yes, it should be inserted in i+1. So there are obviously two things missing - the head and the tail.

        This problem is easy to solve, just compare the ends.

         For example, if the number to be interpolated is smaller than the first one, i.e., num<=data[0], then it will obviously be interpolated at 0, i.e., index=0

         If the number to be interpolated is larger than the last one, i.e. num>=data[length-1], then it is obvious to insert at the end, i.e. index=length

        So think about it all, and finally divide it up into small to big and big to small cases (write a big to small first, small to big just copy him once and all the comparators back)

public:
    //Insert by Value
	void insert(int num)
	{

		if (!rev)//From small to large
		{

			int index;

			//Initialize Insert Subscript
			if (num <= data[0])
			{
				index = 0;
			}

			else if (num >= data[length - 1])
			{
				index = length;
			}

			else
			{
				//Find Insert Location
				for (int i = 0; i < length - 1; i++)
				{
					if (data[i] <= num && num <= data[i + 1])
					{
						index = i+1;
						break;
					}
				}
			}

			//insert
			insert(num, index);
			

		}

		else//From large to small
		{

			//Initialize Insert Subscript
			int index;
			if (num >= data[0])
			{
				index = 0;
			}
			
			else if (num <= data[length - 1])
			{
				index = length;
			}

			else
			{
				//Find Insert Location
				for (int i = 0; i < length - 1; i++)
				{
					if (data[i] >= num && num >= data[i + 1])
					{
						index = i+1;
						break;
					}
				}
			}

			//insert
			insert(num, index);

		}

	}

This completes the SeqList class

The code for the entire class is as follows:

class SeqList
{
	
public:
	//No parameter construct, that is, construct an empty linear table
	SeqList()
	{
		length = 0;
		rev = false;//The default is to hit big from small
	};

	//Construction with parameters, reverse stands for reverse sort order, default from small to large
	SeqList(int a[], int n, bool reverse = false)
	{
		rev = reverse;
		length = n;
		//Quickly arrange the given array
		sort(a, a + n);
		if (!reverse)
		{
			for (int i = 0; i < n; i++)
				data[i] = a[i];
		}
		else//Assign data in reverse order
		{
			for (int i = 0; i < n; i++)
			{
				data[i] = a[n - 1 - i];
			}
		}
	};
	
	//Determine if the table is empty
	bool empty()
	{
		return (length == 0) ? true : false;
	}

	//Get the stored data series
	void get_data(int a[])
	{
		for (int i = 0; i < length; i++)
			a[i] = data[i];
	}

	//Get Length
	int get_length()
	{
		return length;
	}

	//Bitwise deletion of elements
	void del_index(int index)
	{

		if (index<0 || index>length - 1)
		{
			cout << "Subscript overflow, cannot be deleted!" << endl;
			throw 1;
		}

		for (int i = index; i < length - 1; i++)
		{
			data[i] = data[i + 1];
		}
		length--;//Length-1

	}

	//Delete elements by value
	void del_num(int num, bool all = false)
	{

		if (!all)
		{
			int index = get_num(num);

			if (index == -1)
			{
				cout << "Delete failed! There are no elements in the linear table" + to_string(num) << endl;
				throw 1;
			}
			
			del_index(index);

		}
		
		else
		{
			int index = get_num(num);

			if (index == -1)
			{
				cout << "Delete failed! There are no elements in the linear table" + to_string(num) << endl;
				throw 1;
			}

			//Delete all when found
			int ind[MaxSize];//Anti-heavenly is all a number
			int count = 0;
			for (int i = index; i < length; i++)
			{
				if (data[i] == num)
				{
					ind[count] = i;
				}
			}
			//Delete
			for (int i = 0; i <= count; i++)
			{
				del_index(ind[i]-i);
			}

		}

	}

	//Bit Acquisition
	int get_index(int index)
	{
		if (index<0 || index>length - 1)
		{
			cout << "Given subscript overflow range!" << endl;
			throw 1;
		}
		else
		{
			return data[index];
		}
	}

	//Get by value
	int get_num(int x)
	{
		int index = -1;//Return to -1 if not found
		for (int i = 0; i < length; i++)
		{
			if (data[i] == x)
				return i;
		}
		return index;
	}

	//Bitwise insertion
	void insert(int num, int index)
	{

		if (index<0 || index>length)
		{
			cout << "Given subscript overflow range!" << endl;
			throw 1;
		}

		else
		{
			if (index != length)
			{
				for (int j = length; j >= index + 1; j--)
					data[j] = data[j - 1];
				data[index] = num;
				length++; //Length after insertion+1
			}
			else
			{
				data[length] = num;
				length++;
			}
			
		}

	}

	//Insert by value (Task 1)
	void insert(int num)
	{

		if (!rev)//From small to large
		{

			int index;

			//Initialize Insert Subscript
			if (num <= data[0])
			{
				index = 0;
			}

			else if (num >= data[length - 1])
			{
				index = length;
			}

			else
			{
				//Find Insert Location
				for (int i = 0; i < length - 1; i++)
				{
					if (data[i] <= num && num <= data[i + 1])
					{
						index = i+1;
						break;
					}
				}
			}

			//insert
			insert(num, index);
			

		}

		else//From large to small
		{

			//Initialize Insert Subscript
			int index;
			if (num >= data[0])
			{
				index = 0;
			}
			
			else if (num <= data[length - 1])
			{
				index = length;
			}

			else
			{
				//Find Insert Location
				for (int i = 0; i < length - 1; i++)
				{
					if (data[i] >= num && num >= data[i + 1])
					{
						index = i+1;
						break;
					}
				}
			}

			//insert
			insert(num, index);

		}

	}

	//Show Linear Table
	void show()
	{

		cout << "The linear table length is" << length << endl;
		string sort_func = (rev) ? "From large to small" : "From small to large";
		cout << "The linear table is arranged as" << sort_func << endl;
		for (int i = 0; i < length; i++)
		{
			cout << "No." << i + 1 << "Elements are:" << data[i] << endl;
		}

	}

	bool get_rev()
	{
		return rev;
	}

private:
	int length;  //Linear Table Length
	int data[MaxSize]; //Data stored in an array
	bool rev; //Judging from small to large or from large to small
};

Last Teacher's Task - Merging Linear Tables and Keeping them Progressive

         This function is divided into two cases, weightless and non-weighted. The exception is that the two tables to be merged are sorted differently and cannot be merged at this time.

        First merge - merging is actually inserting each element of a table into another by value

        Again, weighting - del_for each repeating element Num (num, true) is fine (which is why deleting by value is also deleted completely and deleted separately)

        The code is as follows:

//Merge Bilinear Tables
SeqList combine(SeqList s1, SeqList s2, bool sift = false)//Default No Weighting
{

	//Sort differently then cannot merge
	if (s1.get_rev() != s2.get_rev())
	{
		cout << "Bilinear tables are sorted differently and cannot be merged!" << endl;
		throw 1;
	}

	if (!sift)//No Weighting
	{
		cout << "The result of not merging the bilinear tables is:" << endl;
		//Insert the shorter ones into the longer ones
		if (s2.get_length() < s1.get_length())
		{

			int end = (s2.get_length() % 2 == 0) ? s2.get_length() / 2 : s2.get_length() / 2 + 1;
			for (int i = 0; i < end; i++)
			{
				s1.insert(s2.get_index(i));
				if (!((s2.get_length() % 2 != 0)&&(i!= s2.get_length()/2)))
					s1.insert(s2.get_index(s2.get_length() - 1 - i));
			}

			return s1;

		}

		else
		{

			int end = (s1.get_length() % 2 == 0) ? s1.get_length() / 2 : s1.get_length() / 2 + 1;
			for (int i = 0; i < end; i++)
			{
				s2.insert(s1.get_index(i));
				if (s1.get_length() - 1 - i != i)
					s2.insert(s1.get_index(s1.get_length() - 1 - i));
			}

			return s2;

		}

	}
	else//Duplicate removal
	{
		cout << "The result of de-merging a bilinear table is:" << endl;
		//Insert the shorter ones into the longer ones
		if (s2.get_length() < s1.get_length())
		{

			//Duplicate removal
			for (int i = 0; i < s2.get_length(); i++)
			{
				//If repeating, insert into the array delete then insert into the inserted array
				if (s1.get_num(s2.get_index(i)) != -1)
				{
					s2.del_num(s2.get_index(i), true);
				}
			}

			int end = (s2.get_length() % 2 == 0) ? s2.get_length() / 2 : s2.get_length() / 2 + 1;
			for (int i = 0; i < end; i++)
			{
				s1.insert(s2.get_index(i));
				if (s2.get_length() - 1 - i != i)
					s1.insert(s2.get_index(s2.get_length() - 1 - i));
			}

			return s1;

		}

		else
		{

			//Duplicate removal
			for (int i = 0; i < s1.get_length(); i++)
			{
				//If repeating, insert into the array delete then insert into the inserted array
				if (s2.get_num(s1.get_index(i)) != -1)
				{
					s1.del_index(i);
				}
			}

			int end = (s1.get_length() % 2 == 0) ? s1.get_length() / 2 : s1.get_length() / 2 + 1;
			for (int i = 0; i < end; i++)
			{
				s2.insert(s1.get_index(i));
				if (s1.get_length() - 1 - i != i)
					s2.insert(s1.get_index(s1.get_length() - 1 - i));
			}

			return s2;

		}

	}

}

Test function

        Call in main function to see our results!

void test()
{

	int a[] = { 1, 3, 4, 2, 6, 5 };
	int b[] = { 8, 9, 12, 10, 7, 11 };

	SeqList s1(a, sizeof(a) / 4, true), s2(b, sizeof(b) / 4, true), * ptr;

	ptr = &s1;
	int temp[MaxSize];
	ptr->get_data(temp);
	cout << "The linear table stores the following sequence data:" << endl;
	for (int i = 0; i < s1.get_length(); i++)
		cout << "No." << i + 1 << "Elements are:" << temp[i] << endl;
	ptr->insert(20);
	ptr->insert(0);
	ptr->insert(15);
	ptr->show();
	ptr = &s2;
	ptr->insert(30);
	ptr->insert(0);
	ptr->insert(15);
	ptr->show();
	SeqList combined = combine(s1, s2);
	ptr = &combined;
	ptr->show();
	combined = combine(s1, s2, true);
	ptr->show();

	//Exception test (two tables arranged differently cannot be merged)
	int c[] = {1,2,5,9,7,46,84};
	SeqList s3(c, sizeof(c)/4);
	ptr = &s3;
	ptr->show();
	combine(s1, s3);

}

Run Results

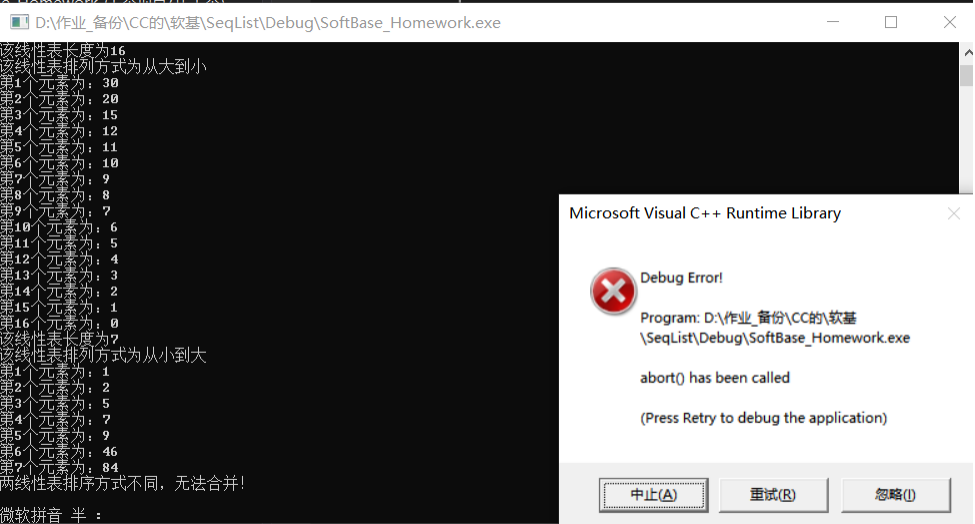
  Finish scattering flowers!