Heap sort

Heap is a complete binary tree with the following properties: the value of each node is greater than or equal to the value of its left and right child nodes, which is called the large top heap (also called the maximum heap); or the value of each node is less than or equal to the value of its left and right child nodes, which is called the small top heap (also called the minimum heap).

The minimum and maximum heaps are as follows:

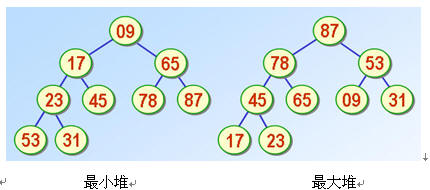
It can be found that the root node must be the largest (smaller) of all nodes in the heap.

The basic idea of heap sorting (taking the big top heap as an example): the sequence to be sorted forms a big top heap. At this point, the maximum value of the whole sequence is the root node of the heap top. Remove it (in fact, exchange it with the end element of the heap array, at this time, the end element is the maximum value), and then reconstruct the remaining n-1 sequences into a heap, so as to get the next largest value of n elements. If we do this repeatedly, we can get an ordered sequence.

The thought use case diagram of heap sorting is explained as follows:

1. The establishment process of the initial minimum heap (gradually adjusted to the minimum heap from the bottom to the top)

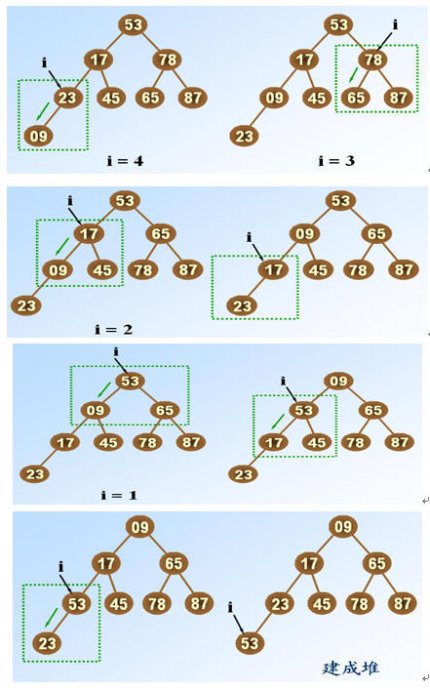
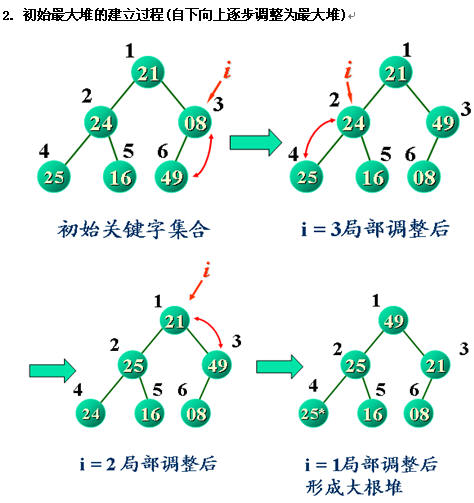
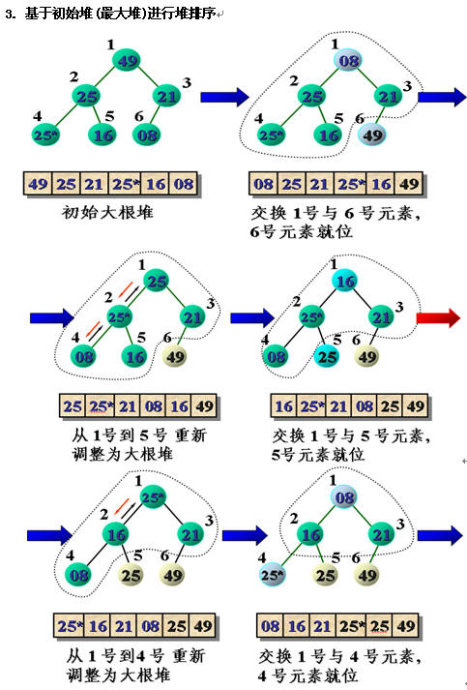
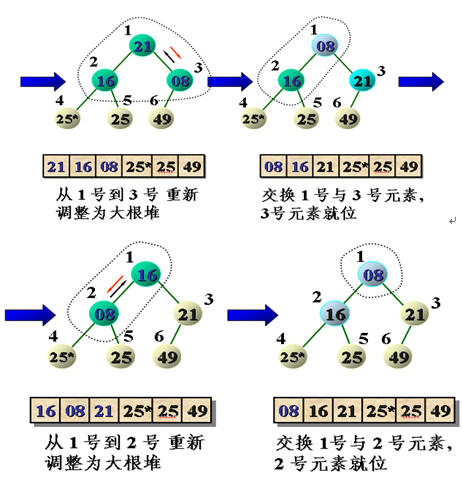
The specific code is as follows:

1. Some preparations before sorting, and establish the structure needed for proper sorting.

/********* Sort struct. H************/
#define MAXSIZE 100 / / maximum number of arrays to sort

class SqList{
public:
	int r[MAXSIZE+1];
	int length;
};

/* Exchange values of array r in L with index i and j */
void swap(SqList *L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}

/* Show array contents */
void showSqList(SqList *L)
{
	for(int i=1;i<=L->length;i++)
		std::cout<<L->r[i]<<"  ";
	std::cout<<std::endl;
}

2. Write the main file to realize sorting and testing.

/********* C++Heap sorting algorithm************/
#include<iostream>
#include<time.h>
#include"sort_struct.h"
using namespace std;

/* This function adjusts the keywords of L - > R [S] to make L - > R [S... M] a large top heap. */
void HeapAdjust(SqList *L,int s,int m)
{
	int temp,j;
	temp = L->r[s];
	for(j=2*s;j<=m;j*=2)	//Filter down the child nodes with larger keywords
	{
		if(j<m && L->r[j]<L->r[j+1])
			++j;	//j is the subscript of the older child node in the keyword
		if(temp>=L->r[j])		//If the keywords are greater than the child node, skip
			break;
		L->r[s] = L->r[j];	//Otherwise, exchange key words and contents of older children's nodes
		s = j;
	}
	L->r[s] = temp;		//Insert completed
}

/* Heap sort order table L */
void HeapSort(SqList *L)
{
	int i;
	for (i=L->length/2;i>0;i--)	//Construct r in L into a large top reactor
		HeapAdjust(L,i,L->length);
	
	for (i=L->length;i>1;i--)
	{
		swap(L,1,i);	//Exchange the top of heap record with the last record of the current unsorted subsequence
		HeapAdjust(L,1,i-1);	//Readjust L - > R [1... I-1] to large top reactor
	}
}



int main()
{
	int num[] = {0,50,30,25,15,84,56,34,99,54,111,24,43,6,62,124};
	SqList *L = new SqList;
	L->length = sizeof(num)/sizeof(int)-1;
	for(int i=1;i<=L->length;i++)
		L->r[i] = num[i];
	cout<<"Before sorting:";
	showSqList(L);
	clock_t start = clock();
	HeapSort(L);
	clock_t end = clock();
	double time = ((double)(start-end)) / (double)CLOCKS_PER_SEC * 1000;
	cout<<"After sorting:";
	showSqList(L);
	cout<<"Time consuming:"<<time<<"ms"<<endl;
	return 0;
}

The operation results are as follows:

Because there are too few samples to be sorted, the time consumption is displayed as 0.