Unordered of zipper method_ The map is different from what you think
According to the description of array + zipper method, we can quickly think of the following hash table implemented by zipper method, but is it really so? Let's see how the implementation in the source code is.
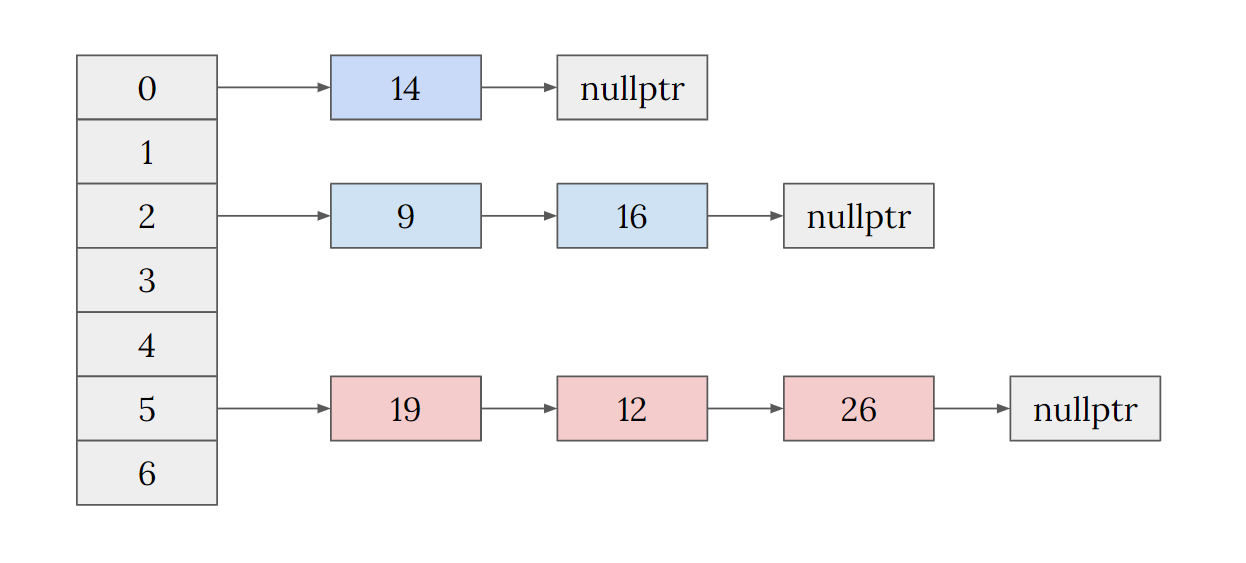
In depth STL source code
The code will not deceive people. You can write a simple code, study the implementation, and then trace and execute through gdb:
#include <vector>
#include <unordered_map>
int main() {
std::unordered_map<int, int> hashmap;
hashmap[26] = 26;
}
Compile and open gdbgui:
g++ -g hashmap.cc -std=c++11 -o hashmap_test gdbgui -r -p 8000 ./hashmap_test
gdb follows up and finds that the code will go to hashtable_ policy. In the operator [] function of H, I simplified the code and extracted only the key code:
auto operator[](const key_type& __k) -> mapped_type&
{
__hashtable* __h = static_cast<__hashtable*>(this);
// Get hashcode according to key
__hash_code __code = __h->_M_hash_code(__k);
// Get the index of the bucket according to the key and hashcode: n
std::size_t __n = __h->_M_bucket_index(__k, __code);
// Try to find the node with node key k in bucket n
__node_type* __p = __h->_M_find_node(__n, __k, __code);
if (!__p)
{
// If the node found is nullptr, a node is reassigned and the new node is inserted into the hash table.
__p = __h->_M_allocate_node(k);
return __h->_M_insert_unique_node(__n, __code, __p)->second;
}
return __p->_M_v().second;
}
The function of the operator [] function is to calculate the hash value of the key, find the corresponding bucket n through the hash value, and finally find whether there is a node with key=k in this bucket,
If the required node is not found, a new node is assigned and inserted.
So how is this node inserted? Insert function under_ h->_ M_ insert_ unique_ node(__n, __code, __p):
auto _M_insert_unique_node(__bkt, __code, __node, size_type __n_elt = 1) -> iterator
{
// Determine whether rehash is required
const __rehash_state& __saved_state = _M_rehash_policy._M_state();
std::pair<bool, std::size_t> __do_rehash
= _M_rehash_policy._M_need_rehash(_M_bucket_count, _M_element_count,
__n_elt);
if (__do_rehash.first)
{
_M_rehash(__do_rehash.second, __saved_state);
__bkt = _M_bucket_index(this->_M_extract()(__node->_M_v()), __code);
}
this->_M_store_code(__node, __code);
// Always insert at the beginning of the bucket.
// Insert the node into the beginning of the bucket
_M_insert_bucket_begin(__bkt, __node);
++_M_element_count;
return iterator(__node);
}
_ M_ insert_ unique_ The node () insertion function is mainly used to judge whether the load of the hash table will be too high if a new node is inserted? Do you need to re expand the capacity? Pass after the expansion is completed_ M_insert_bucket_begin() is then inserted into the begin position of the bucket. We won't pay attention to the rehash process here for the time being. Let's take a look at it first_ M_ insert_ bucket_ How to implement the function begin():
_M_insert_bucket_begin(size_type __bkt, __node_type* __node)
{
// Judge whether bucket n is empty
if (_M_buckets[__bkt])
{
// Bucket is not empty, we just need to insert the new node
// after the bucket before begin.
// If the bucket is not empty, use the header insertion method to insert the node into the beginning
__node->_M_nxt = _M_buckets[__bkt]->_M_nxt;
_M_buckets[__bkt]->_M_nxt = __node;
}
else
{
// The bucket is empty, the new node is inserted at the
// beginning of the singly-linked list and the bucket will
// contain _M_before_begin pointer.
// If the node is not empty,
__node->_M_nxt = _M_before_begin._M_nxt;
_M_before_begin._M_nxt = __node;
if (__node->_M_nxt)
// If__ node->_ M_ NXT is the original_ M_before_begin._M_nxt is not empty,
// Then you have to_ M_before_begin._M_nxt points to the new node _.
// We must update former begin bucket that is pointing to
// _M_before_begin.
_M_buckets[_M_bucket_index(__node->_M_next())] = __node;
// Will_ M_before_begin is assigned to bucket n.
_M_buckets[__bkt] = &_M_before_begin;
}
}
Now comes the wonderful part of inserting the node. Whether the current bucket is empty divides the function into two parts. Next, the whole inserting process will be shown in the way of a legend.
Insert first node
First, let's look at the empty case:
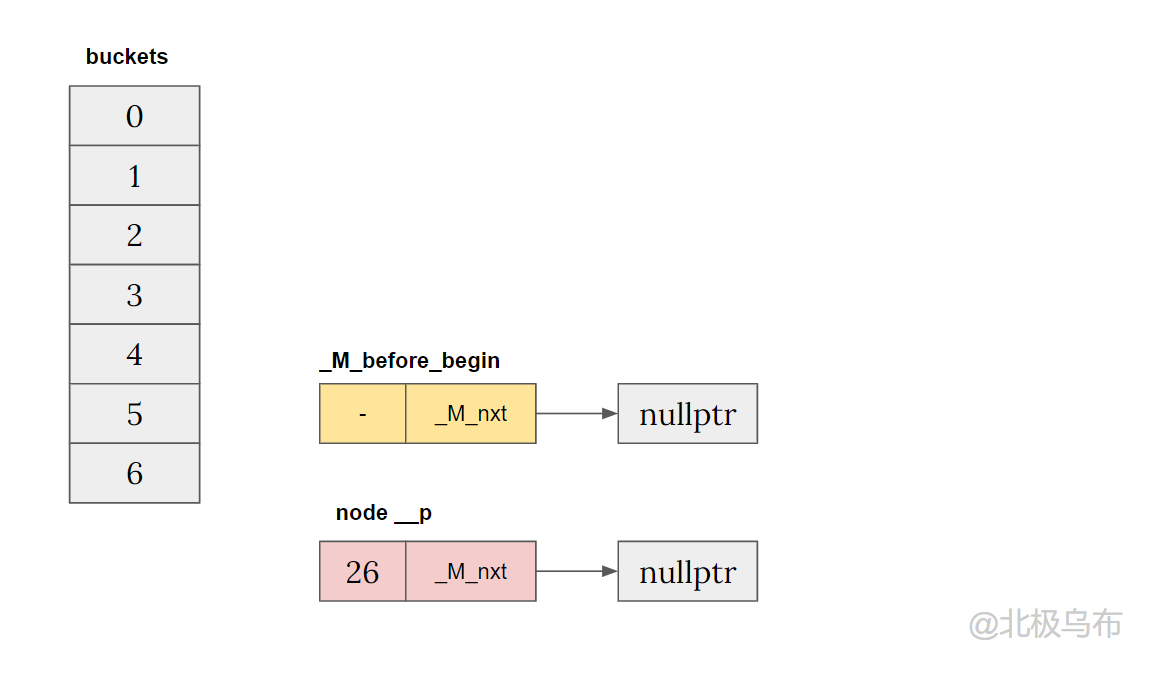
Before entering the function, there are:
- Pre created (hashmap constructor) buckets
- A member variable_ M_before_begin
- A newly assigned insertion node__ p
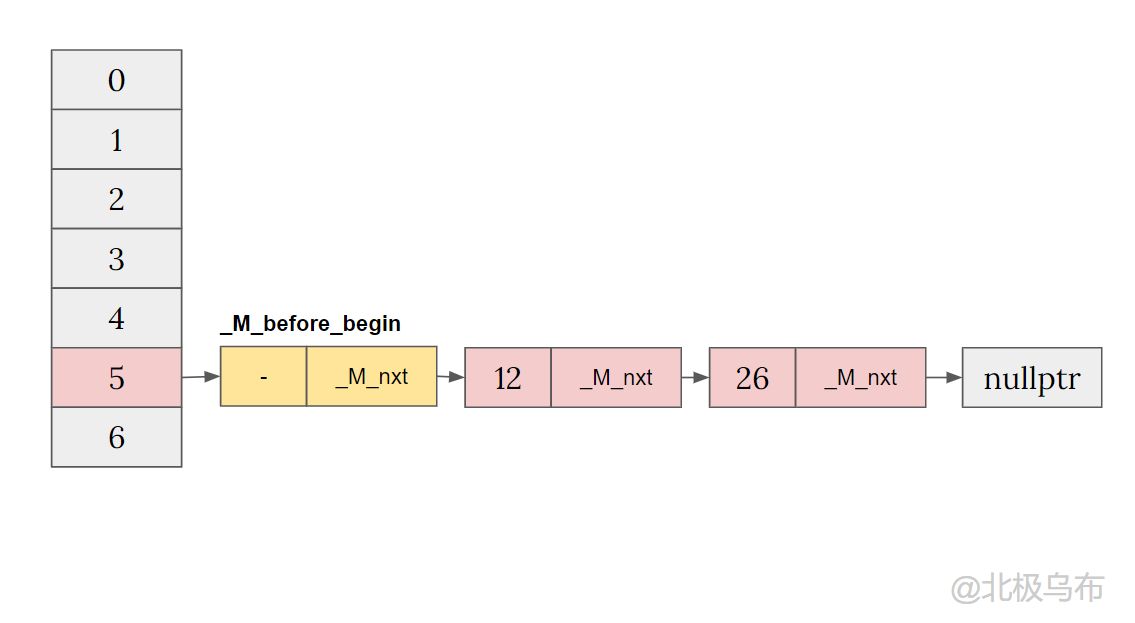
The currently inserted value is 26. After hash calculation, n = 26% 7 = 5 will be inserted in bucket[5]:

When bucket[5] is empty, the insertion code is:
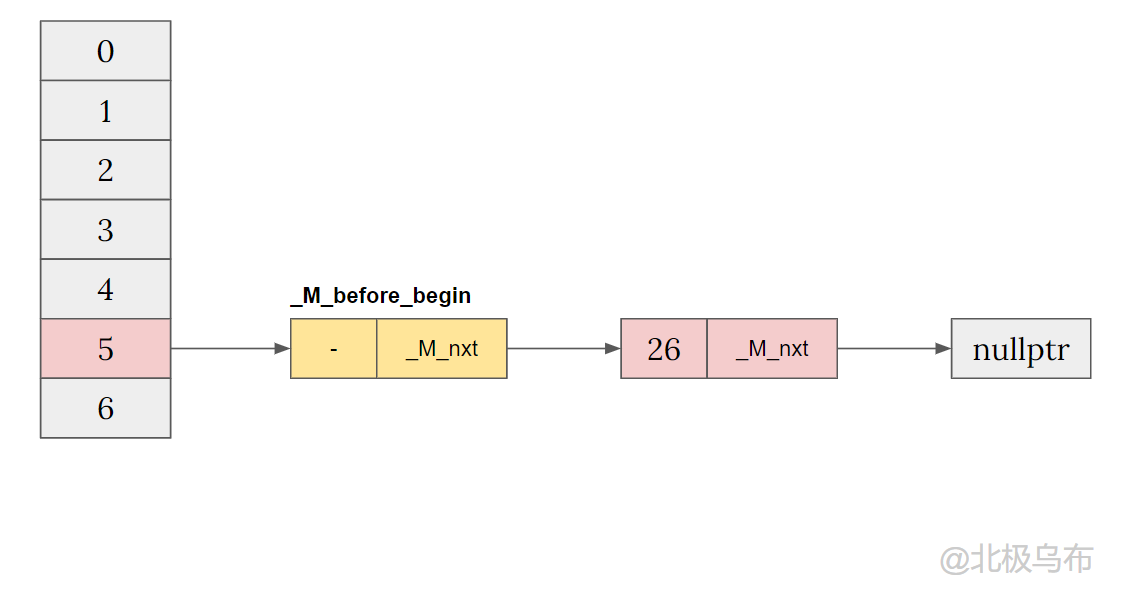
__node->_M_nxt = _M_before_begin._M_nxt; // ① _M_before_begin._M_nxt = __node; // ② if (__node->_M_nxt) _M_buckets[_M_bucket_index(__node->_M_next())] = __node; _M_buckets[__bkt] = &_M_before_begin; // ③
- ① ② the two steps are the header insertion method of the classic linked list, which is inserted between the two nodes.
- Because here__ node->_ M_ NXT refers to nullptr, and the specific logic is skipped first.
- Then step ③_ M_ before_ The address of begin is assigned to bucket[n]
So we get a linked list after header insertion:
Insert the second node of the same bucket
If you try to insert a new value into the same bucket, because the current bucket has a value, the code will go to_ M_ insert_ bucket_ The first half of the function begin():
if (_M_buckets[__bkt])
{
// Bucket is not empty, we just need to insert the new node
// after the bucket before begin.
// If the bucket is not empty, use the header insertion method to insert the node into the beginning
__node->_M_nxt = _M_buckets[__bkt]->_M_nxt;
_M_buckets[__bkt]->_M_nxt = __node;
}
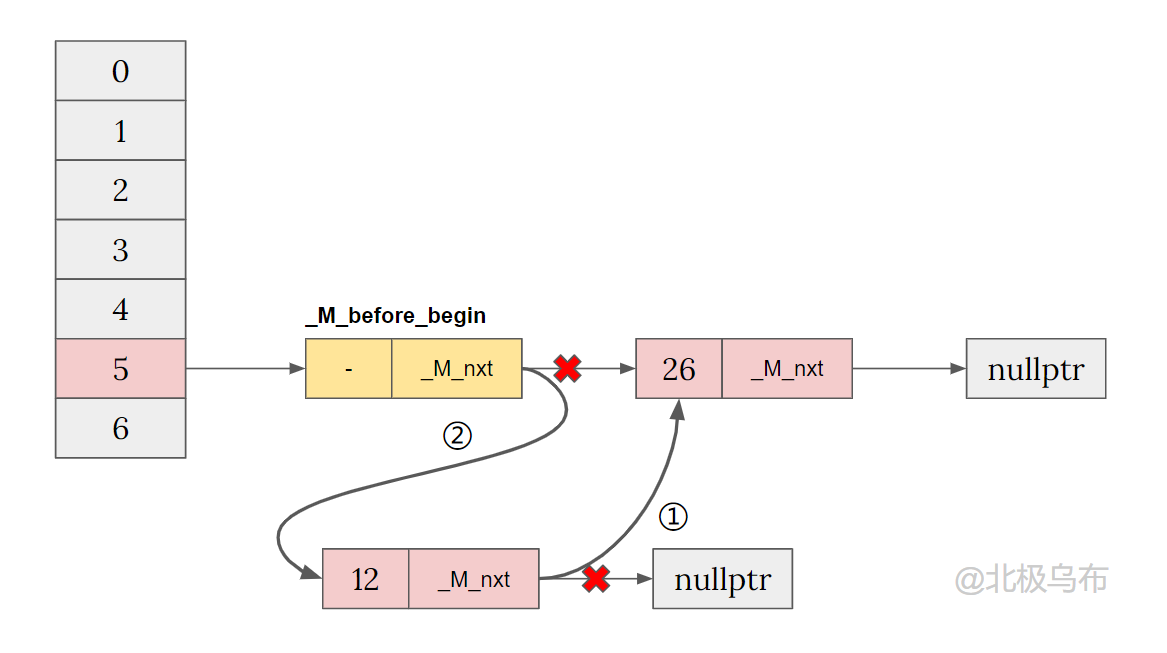
Simplified to:
So far, the hash table is almost the same as that in the imagination. It is constantly inserted into one bucket and connected with a linked list. Now try to insert a node into another bucket:
Insert a node in a different bucket
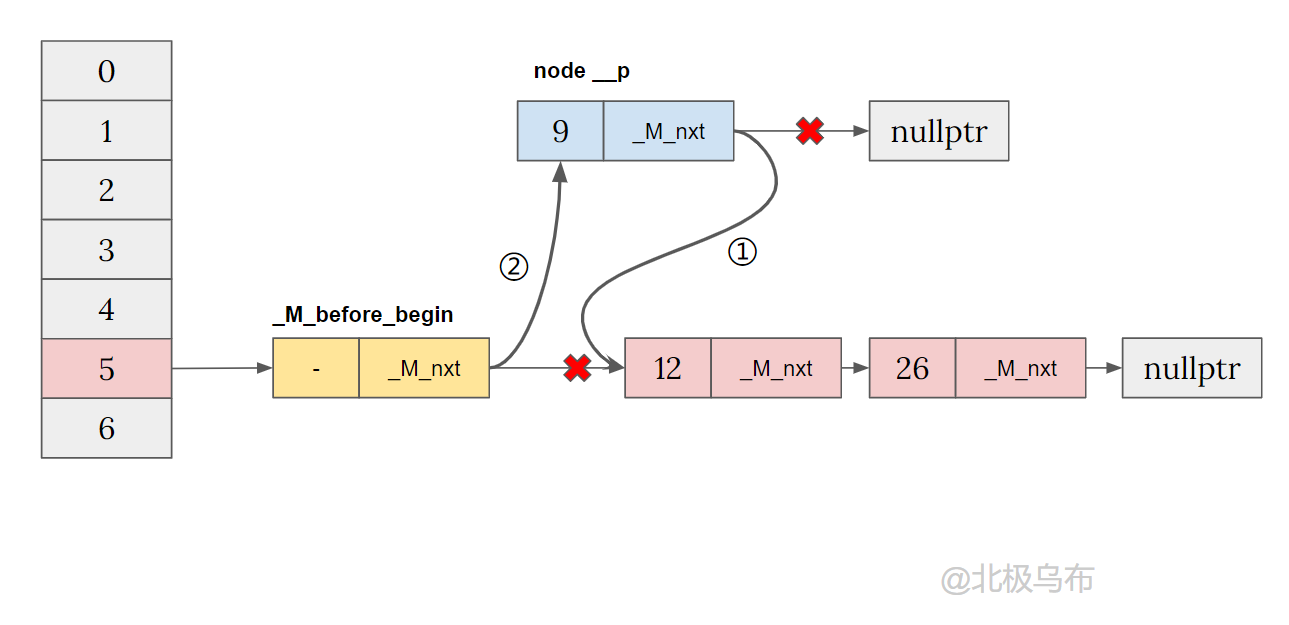
The first two lines with empty bucket will be run first, which is still the result of header insertion:
__node->_M_nxt = _M_before_begin._M_nxt; _M_before_begin._M_nxt = __node;
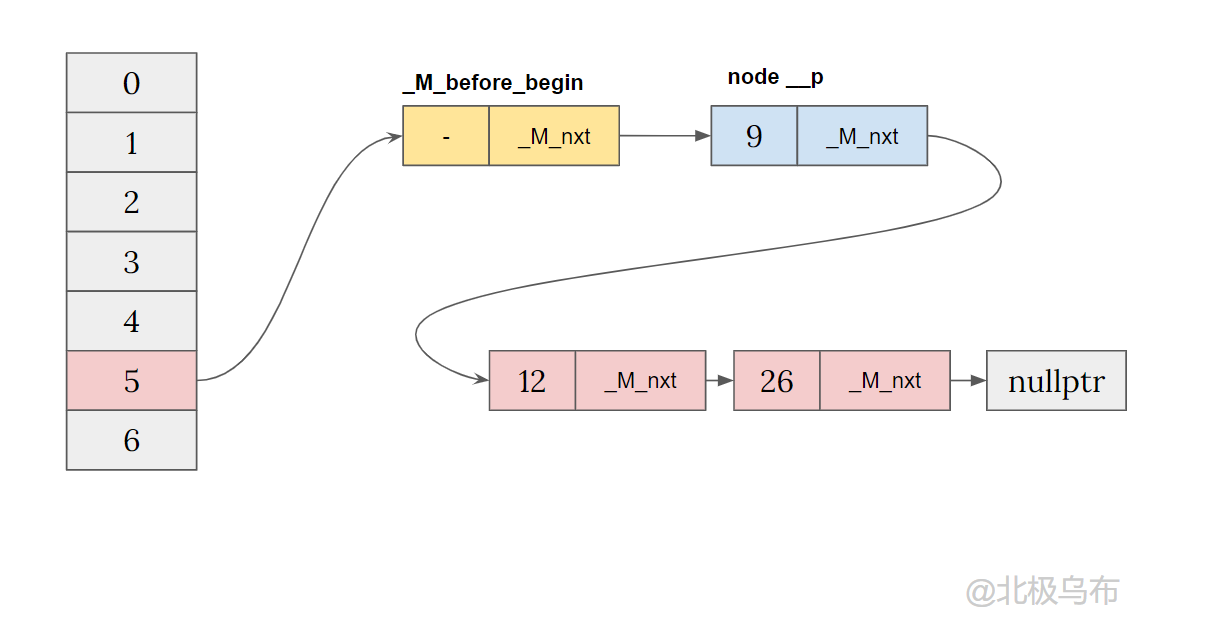
Continue with the following statement:
if (__node->_M_nxt) // We must update former begin bucket that is pointing to // _M_before_begin. _M_buckets[_M_bucket_index(__node->_M_next())] = __node; _M_buckets[__bkt] = &_M_before_begin;
At this point, because_ M_before_begin._M_nxt is not empty and assigned to a new node__ Node_ M_ On NXT, the logic will be executed:
_M_buckets[_M_bucket_index(__node->_M_next())] = __node;
__ node->_ M_ Next () is the bucket of the node whose key is 12_ The index should be 5, so the pointer of bucket[5] will point to the newly inserted node.
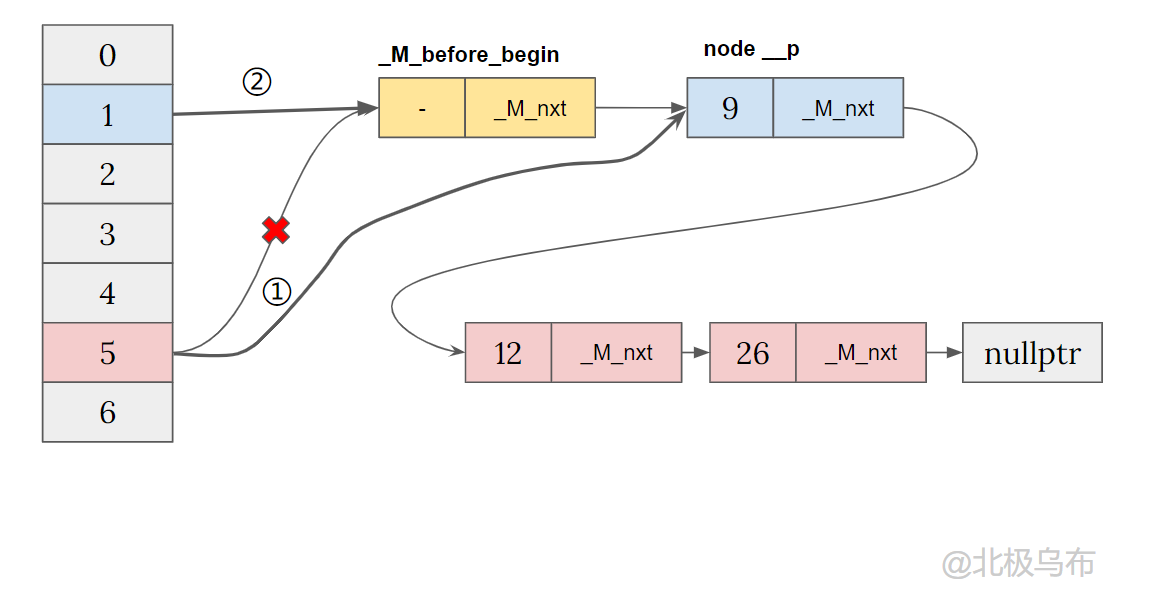
Finally, point bucket[1] to_ M_before_begin, get:
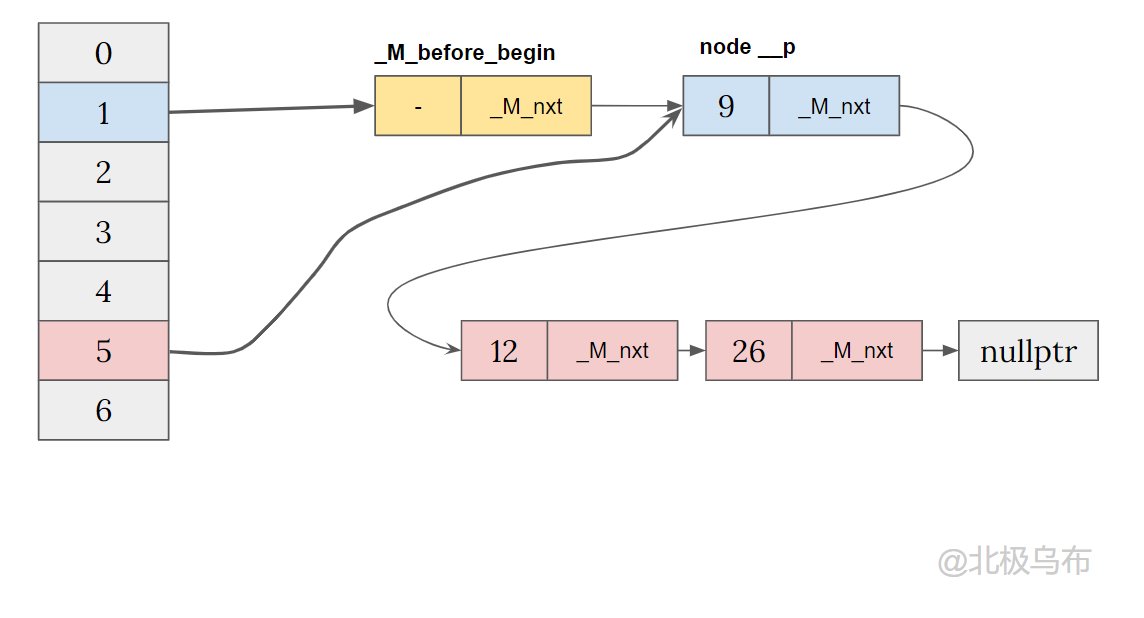
If you continue to simplify, you will eventually form a single linked list with sentinel nodes, and each bucket only has a pointer to the corresponding position of the linked list, where_ M_before_begin is the sentinel node:
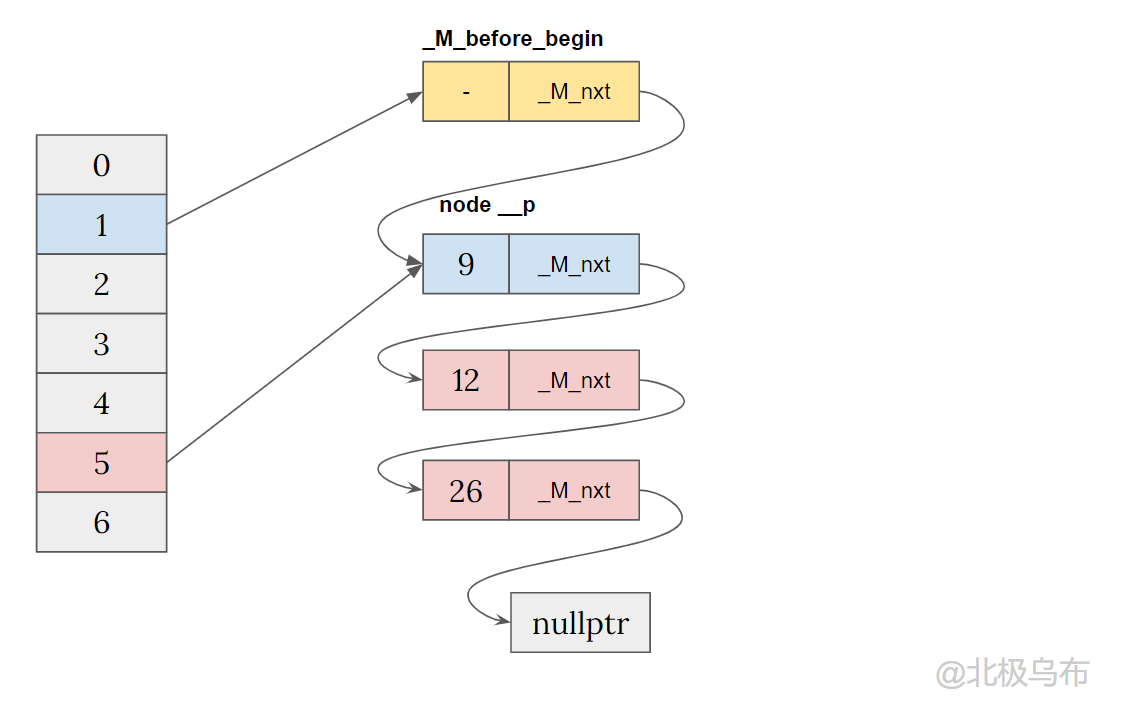
Final structure
- When a bucket has a value, it is inserted into the corresponding bucket through the previous pointer and header insertion method.
- If the bucket has no value, the sentinel node will be switched to the new bucket.
For example:
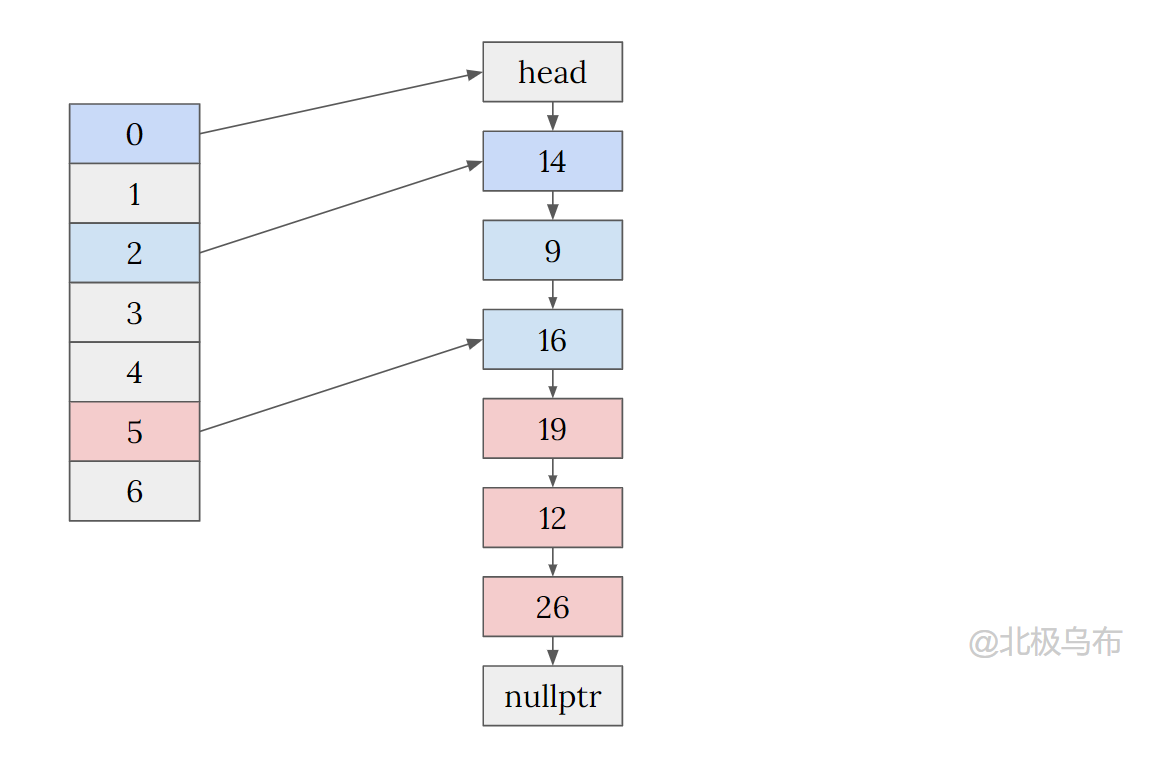
What's the advantage of being so complicated?
The time complexity of traversal.
Suppose that in this implementation, traversing the entire hashmap only needs to move from the head pointer to nullptr like head - > next. If there are n elements and k bucket s in total, the time complexity is only O(n).
What if it was the first implementation? Each bucket has a linked list. You need to judge whether all buckets are empty, and traverse the linked list in each bucket. The time complexity will reach O(n + k). Moreover, in order to avoid hash conflict, the hash table usually has a relatively large array, and the influence of K in the expression is very large.
verification
The inserted code has been understood. Verify whether the understood structure is true, and then take a look at HashMap The code of find (key). The process of find is in HashMap There are already nodes in operator []. Judge whether there are nodes before inserting:
auto operator[](const key_type& __k) -> mapped_type&
{
__hashtable* __h = static_cast<__hashtable*>(this);
// Get hashcode according to key
__hash_code __code = __h->_M_hash_code(__k);
// Get the index of the bucket according to the key and hashcode: n
std::size_t __n = __h->_M_bucket_index(__k, __code);
// Try to find the node with node key k in bucket n
__node_type* __p = __h->_M_find_node(__n, __k, __code);
if (!__p)
{
// ... Do allocate and insert
}
return __p->_M_v().second;
}
Trace function__ h->_ M_ find_ Node (_n, _k, _code), will call_ M_find_before_node(__n, __k, __code):
auto _M_find_before_node(size_type __n, const key_type& __k, __hash_code __code) const -> __node_base*
{
// _ M_buckets[__n] stores the prev of the bucket. If it does not exist, the bucket is empty
__node_base* __prev_p = _M_buckets[__n];
if (!__prev_p)
return nullptr;
// Start with prev - > next and cycle until prev - > next is nullptr or the bucket number of prev - > next is not the current bucket.
for (__node_type* __p = __prev_p->_M_nxt; ; __p = __p->_M_next())
{
if (this->_M_equals(__k, __code, __p))
return __prev_p;
// Cycle end judgment
if (!__p->_M_nxt || _M_bucket_index(__p->_M_next()) != __n)
break;
__prev_p = __p;
}
return nullptr;
}
Now judge whether the current bucket[n] has a value. If it has a value, start traversing from prev - > next to nullptr, or the bucket number is not the node of the current bucket.
For example, find the start and end of a node in bucket[2]:
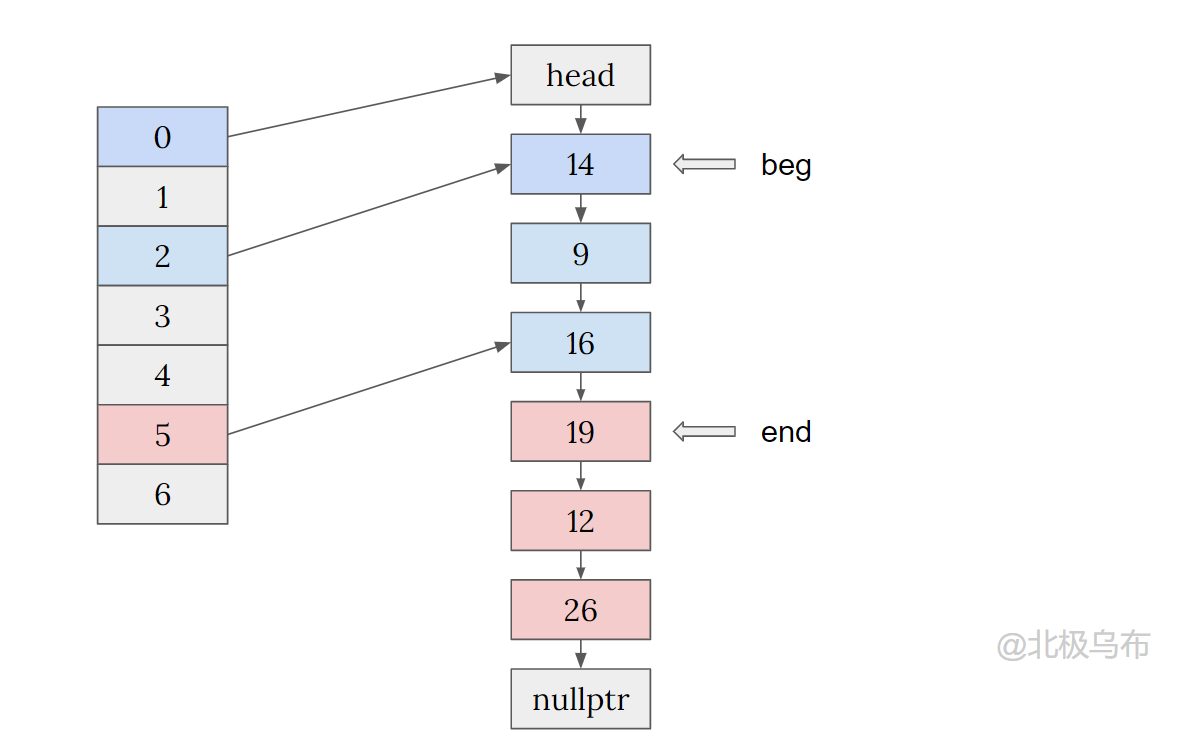
summary
The implementation of STL in the standard library is still very Amazing. It has three implementation keywords, array, single linked list and sentinel node. It also supports the traversal complexity of O(n) when it supports bucket division.
Also attached is my reference link:
- Helped me understand_ M_ before_ Function of begin node https://szza.github.io/2021/03/01/C++/2_/