I have been a novice for many years

preface

The law of planetary operation in the solar system has long been thoroughly studied by predecessors. Regional meteorology and building daylighting are more applied to the law of solar operation relative to the earth. Recently, some research has been done on the calculation of solar radiation based on regional observation values for the duration of regional illumination under the shelter of buildings, and the learning process during this period has been recorded.

Basic definition of the first barrier between different disciplines

1, Astronomical knowledge

This paragraph is mainly about definitions

1. Solar altitude angle

It refers to the angle between the incident direction of sunlight and the ground plane at a certain place on the earth

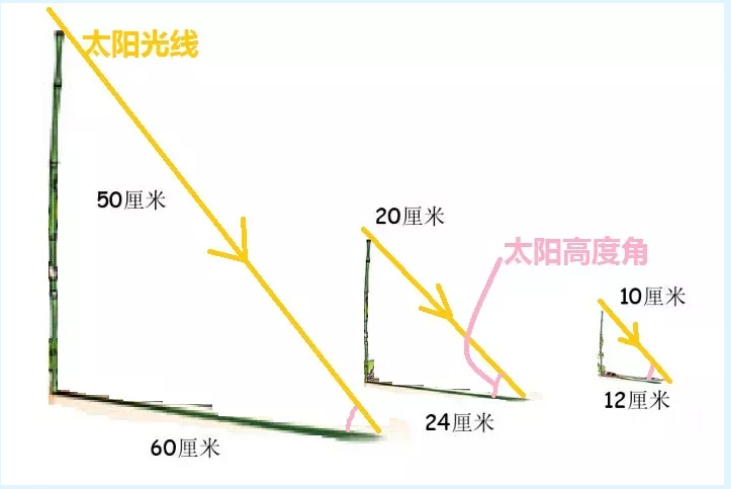
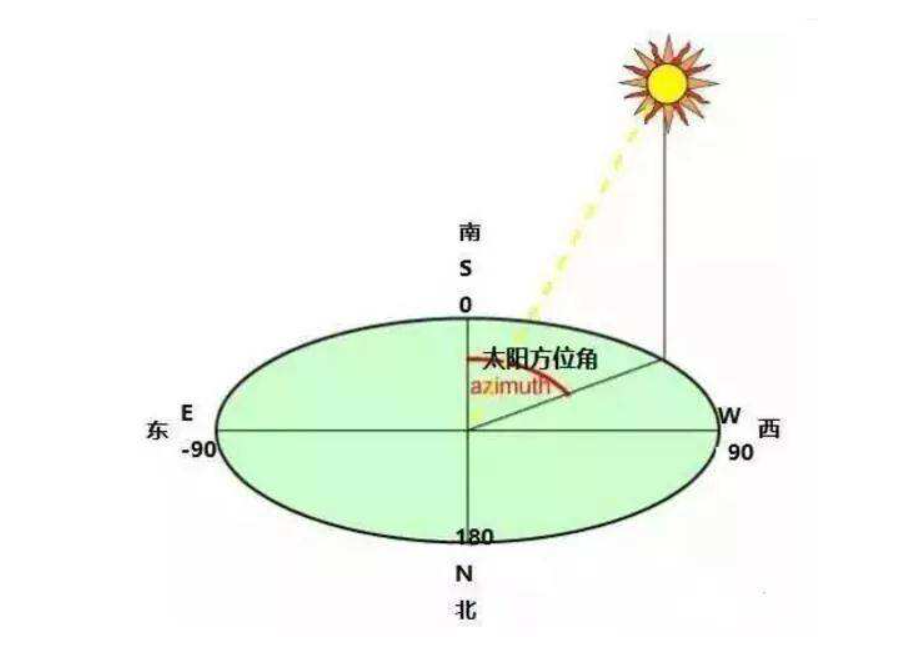
2. Solar azimuth

The angle between the horizontal line facing due south from the observer's location and the projection of the sun's light on the ground plane is usually specified as positive in the morning and negative in the afternoon.

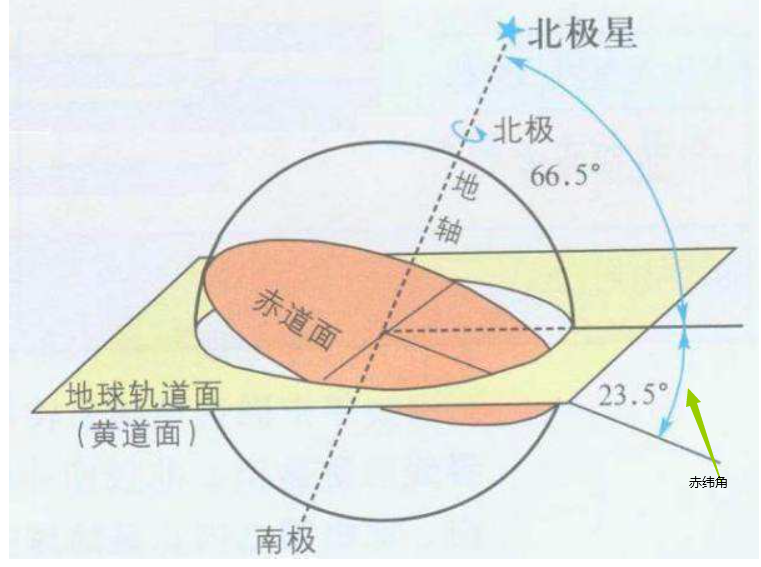
3. Declination angle

Declination angle, also known as solar declination, is the included angle between the equatorial plane of the earth and the connecting line between the sun and the center of the earth.

4. Time angle

The earth's rotation - cycle is one day, i.e. 24h. There are different time angles at different times, expressed in Ω. The rotation of the earth is 360 °, so the hour angle per hour is 15 °, that is, Ω = 15t, T represents the hours.

There are many definitions. I won't repeat them. The more important ones are the above three.

2, Calculation method

We can see far because we stand on the shoulders of giants

1. Core calculation formula

Solar altitude angle: h s h_{s} hs​:
sin ⁡ ( h s ) = sin ⁡ ( φ ) sin ⁡ ( δ ) + cos ⁡ ( φ ) cos ⁡ ( δ ) cos ⁡ ( Ω ) \sin(h_{s})=\sin(\varphi)\sin(\delta)+\cos(\varphi)\cos(\delta)\cos(\Omega) sin(hs​)=sin(φ)sin(δ)+cos(φ)cos(δ)cos(Ω)
Solar azimuth A s A_{s} As​:
cos ⁡ ( A s ) = sin ⁡ ( h s ) sin ⁡ ( φ ) − s i n ( δ ) cos ⁡ ( h s ) cos ⁡ ( φ ) \cos(A_{s})=\frac{\sin(h_{s})\sin(\varphi)-sin(\delta)}{\cos(h_s)\cos(\varphi)} cos(As​)=cos(hs​)cos(φ)sin(hs​)sin(φ)−sin(δ)​
Geographic latitude: φ \varphi φ
Declination angle: δ \delta δ
δ = 23.45 s i n ( 2 π ∗ 284 + n 365 ) \delta=23.45sin(2\pi*\frac{284+n}{365}) δ= 23.45sin(2 π * 365284+n) (unit: °)
n represents the number of days. January 1 is taken as 1 and December 31 as 365.

Time angle: Ω \Omega Ω
The units of angles should be unified. The following is the formula inserted according to the word system

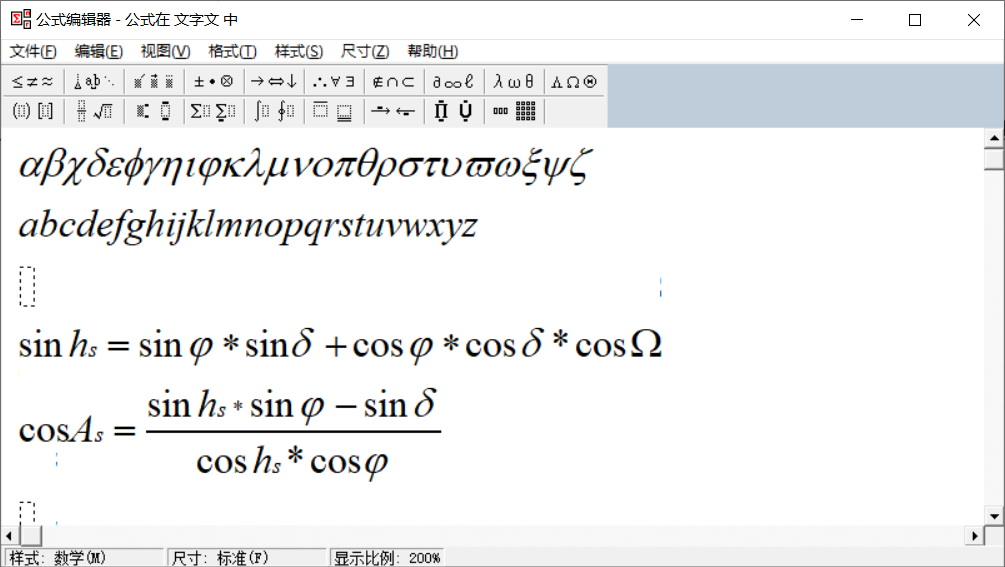
2. Sunrise and sunset time

When the solar altitude angle is 0, the corresponding time angle is the time angle at sunrise and sunset.
corresponding cos ⁡ ( Ω ) = − tan ⁡ ( δ ) tan ⁡ ( φ ) \cos(\Omega)=-\tan(\delta)\tan(\varphi) cos(Ω)=−tan(δ)tan(φ)

After the time angle is calculated, it needs to be converted into the angle system and divided by 15 to get the sunshine duration of half a day; Using 12 + or minus this value is the sunrise and sunset time.

The code is as follows (example):

public class SolarUtil {
    /**
     * Calculate declination angle δ
     * @param day The first day of the year, such as January 1; December 31 365;
     * @return Declination angle
     */
    public static double declination(int day){
        double args = 23.45;
        double season = 2* PI * (284 + day) / 365;
        return args * sin(season);
    }
    
    public static double solarTime2(double latitude,int day){
        // Judge polar day or polar night
        double flag = latitude * SolarUtil.declination(day);
        double t = Math.acos( Math.tan(latitude * Math.PI / 180) * Math.tan(SolarUtil.declination(day) * Math.PI / 180));
        // There is polar day or polar night
        if (Double.toString(t).equals("NaN")){
            if (flag < 0)
                return 0.0;
            else return 180.0;
        }
        double toDegrees = Math.toDegrees(t);
        return toDegrees;
    }
}

3. Average annual light duration

The goal is to calculate the lighting time at each unit on the top of the building, regardless of the complex structure of the building, and deal with it as a simple cuboid.
Package structure

1. Building entities

Define the building with the abscissa and ordinate of the upper left and lower right corners.

package com.dwind.pojo;

import java.util.ArrayList;

/**
 * @author lcdwind
 * @date 2021/10/29 16:54
 */

public class Building {
    private double height;
    private double RDPointX;
    private double RDPointY;
    private double LUPointX;
    private double LUPointY;

    public Building() {
    }

    public Building(double height, double RDPointX, double RDPointY, double LUPointX, double LUPointY) {
        this.height = height;
        this.RDPointX = RDPointX;
        this.RDPointY = RDPointY;
        this.LUPointX = LUPointX;
        this.LUPointY = LUPointY;
    }

    public double getHeight() {
        return height;
    }

    public void setHeight(double height) {
        this.height = height;
    }

    public double getRDPointX() {
        return RDPointX;
    }

    public void setRDPointX(double RDPointX) {
        this.RDPointX = RDPointX;
    }

    public double getRDPointY() {
        return RDPointY;
    }

    public void setRDPointY(double RDPointY) {
        this.RDPointY = RDPointY;
    }

    public double getLUPointX() {
        return LUPointX;
    }

    public void setLUPointX(double LUPointX) {
        this.LUPointX = LUPointX;
    }

    public double getLUPointY() {
        return LUPointY;
    }

    public void setLUPointY(double LUPointY) {
        this.LUPointY = LUPointY;
    }

    @Override
    public String toString() {
        return "Building{" +
                "height=" + height +
                ", RDPointX=" + RDPointX +
                ", RDPointY=" + RDPointY +
                ", LUPointX=" + LUPointX +
                ", LUPointY=" + LUPointY +
                '}';
    }
}

3. Tools

I thought it would be used often, but it didn't really work. On the contrary, I wrote a lot more useless.

package com.dwind.util;

import static java.lang.Math.*;

/**
 * @author lcdwind
 * @date 2021/10/29 15:45
 */
public class SolarUtil {

    // Calculate declination angle δ

    /**
     * Calculate declination angle δ
     * @param day The first day of the year, such as January 1; December 31 365;
     * @return Declination angle
     */
    public static double declination(int day){
        double args = 23.45;
        double season = 2* PI * (284 + day) / 365;
        return args * sin(season);
    }

    /**
     * Convert the local time into the earth rotation angle at the corresponding time
     * @param tureSoloarTime True solar time, for example, 12.5 means 12:30
     * @return Angle timing angle
     */
    public static double hourAngle(double tureSoloarTime){
        return  15.0 * (tureSoloarTime - 12);
    }

    /**
     * Return to the local time corresponding to Beijing time under the corresponding longitude, that is, solar time.
     * @param longitude Calculate the longitude of the position
     * @param CST Beijing time
     * @param day What day of the year
     * @return Local solar time
     */
    public static double trueSoloarTime(double longitude,double CST,double day){
        double B = 2* PI*(day-81) / 364;
        return  CST +(9.87 * sin(2*  B) - 7.53*cos(B) - 1.5*sin(B))/60+ (longitude - 120) / 15.0;
    }

    /**
     *
     * @param longitude Calculate the longitude of the position
     * @param solarTime Local solar time
     * @param day The day of the year is used to correct the differences caused by precession and changes in the earth's rotation
     * @return Beijing time
     */
    public static double CSTTime(double longitude,double solarTime,double day){
        double B = 2* PI*(day-81) / 364;
        return solarTime + (120 - longitude) / 15.0 - (9.87 * sin(2*B) - 7.53*cos(B) - 1.5*sin(B))/60;
    }

    /**
     * Return to solar altitude angle
     * @param latitude Latitude radian system
     * @param declination Declination angle radian system
     * @param hourAngle Time angle radian system
     * @return Solar altitude angle radian system
     */
    public static double solarHight(double latitude, double declination, double hourAngle){
        return asin(sin(latitude) * sin(declination) + cos(latitude) * cos(declination) * cos(hourAngle));
    }

    /**
     * Return sun azimuth
     * @param solarHight Solar altitude angle
     * @param latidude latitude
     * @param declination Declination angle
     * @param time The positive and negative values used to correct the solar azimuth when the local sun is (compared with 12)
     * @return Solar azimuth
     */
    public static double solarAzimuth(double solarHight,double latidude, double declination,double time){

        if (time == 0){
            if(latidude>declination){
                return 0;
            } else {
                return PI;
            }
        }
        double a = (sin(solarHight) * sin(latidude) - sin(declination)) / cos(solarHight) / cos(latidude);
        if (time > 0){
            // Time > 12 means afternoon, and the azimuth is positive.
            return acos(a);
        }else {
            // Time < 12 am, azimuth is negative.
            return -acos(a);
        }

    }


    /**
     * Calculate the solar time angle according to the solar altitude angle
     * @param xDiff Used to calculate the solar altitude angle
     * @param yDiff Used to calculate the solar altitude angle
     * @param highDiff Used to calculate the solar altitude angle
     * @param latitude Latitude here
     * @param day What day of the year
     * @return Angular solar time angle
     */
    public static double solarTime(double xDiff,double yDiff,double highDiff,double latitude,int day){
        double sin_Hs = highDiff / Math.sqrt(xDiff * xDiff + yDiff * yDiff + highDiff * highDiff);


        double flag = Math.sin(latitude * Math.PI / 180)* Math.sin(SolarUtil.declination(day) * Math.PI /180);
        double t = Math.acos(sin_Hs - flag /( Math.cos(latitude * Math.PI / 180) * Math.cos(SolarUtil.declination(day) * Math.PI / 180)));
        if (Double.toString(t).equals("NaN")){
            if (flag < 0)
                return 0.0;
            else return 180.0;
        }
        double toDegrees = Math.toDegrees(t);
        return toDegrees;
    }
    public static double solarTime2(double latitude,int day){

        // Judge polar day or polar night
        double flag = latitude * SolarUtil.declination(day);
        double t = Math.acos( Math.tan(latitude * Math.PI / 180) * Math.tan(SolarUtil.declination(day) * Math.PI / 180));
        // There is polar day or polar night
        if (Double.toString(t).equals("NaN")){
            if (flag < 0)
                return 0.0;
            else return 180.0;
        }
        double toDegrees = Math.toDegrees(t);
        return toDegrees;
    }

    public static double sunDownTime(double latitude, double declination){
        return acos(-tan(latitude)*tan(declination));
    }

    /**
     * On which side of the straight line composed of two points is the judged point, the vector method is used to calculate, and the vector direction is from point 1 to point 2
     * @param x1 Abscissa of point 1
     * @param y1 Point 2 ordinate
     * @param x2 Abscissa of point 2
     * @param y2 Point 2 ordinate
     * @param tempX Abscissa of judged point
     * @param tempY Ordinate of judged point
     * @return Return true to indicate the line or right side, and false to indicate the left side
     */
    public static boolean lineSide(double x1,double y1, double x2,double y2, double tempX,double tempY){

//        if (x2 == x1){
//            return tempX >= x1;
//        }
        if(((tempY-y1)*(x2-x1) - (y2-y1)*(tempX-x1))>0) {
            // left
            return false;
        }else {
            // Line or right
            return true;
        }

    }

    /**
     * Returns whether the judgment point is inside the polygon
     * @param points Polygon vertex array
     * @param tempX Abscissa of judgment point
     * @param tempY Ordinate of judgment point
     * @return true inside or above the polygon, false outside
     */
    public static boolean isCovered(double[][] points,double tempX,double tempY){
        boolean flag = true;
        for (int i =0;i<points.length-1;i ++){
            boolean b = lineSide(points[i][0], points[i][1], points[i + 1][0], points[i + 1][1], tempX, tempY);
            if (!b){
                flag = false;
                break;
            }
        }
        return flag;
    }
}

4. Calculation part

package com.dwind.building;

import com.dwind.pojo.Building;
import com.dwind.util.SolarUtil;

import java.util.ArrayList;
import java.util.HashMap;

/**
 * @author lcdwind
 * @date 2021/10/29 16:35
 */
public class Sunshine {
    public HashMap<Building, Double> sunTime(Building target, ArrayList<Building> buildings, double latitude, double longitude) {
        HashMap<String, Double> map = new HashMap<>();
        // It is used to record the average annual illumination time of each small unit
        HashMap<Building, Double> cubeMap = new HashMap<>();
        // Unit length of segmentation
        double cube = 1.0;
        // target is divided into small cell cube s;
        ArrayList<Building> buildingCube = new ArrayList<>();
        for (double xMark = target.getLUPointX(), yMark = target.getRDPointY(); yMark < target.getLUPointY(); yMark += cube) {
            for (; xMark < target.getRDPointX(); xMark += cube) {
                Building building = new Building(target.getHeight(), xMark + cube, yMark, xMark, yMark + cube);
                buildingCube.add(building);
            }
            xMark = target.getLUPointX();
        }


        // Calculate the annual average illumination of each small area in a cycle
        for (Building building : buildingCube) {
            map.put("sunHour", 0.0);
            // Cycle the daily illumination
            for (int day = 1; day <= 365; day++) {

//Is there any difference between the shelter in the east or west of the building?
                // Here, it is not accurate to judge only the height angle, and the obstructions on the left and right sides of the target building are not distinguished, and the two will be covered by the highest and most recent results.
                // One idea is to calculate the sunshine shadow time change of the day according to the light shadow bar length diagram of the building, then analyze it according to three situations, and finally take the point of the center value as the marker point is also a good method

                // sunUpTime angle of sunrise
                double sunUpTime = SolarUtil.solarTime(1, 1, 0, latitude, day);
                // sunUP,sunDown sunrise and sunset
                double sunUp = 12 - sunUpTime / 15;
                double sunDown = 12 + sunUpTime / 15;
                // The time of the day when there is no shelter.
                double noCoverTime = 0;
                // Sample every 0.01 * 60 minutes to judge whether the target position is covered
                for (double time = sunUp; time <= sunDown; time += 0.01) {
                    boolean total = true;
                    // Judge the occlusion one by one
                    for (Building value : buildings) {
                        // Altitude difference, solar altitude angle, solar azimuth, shadow polygon array
                        double highDiff = value.getHeight() - building.getHeight();
                        double sunHeight = SolarUtil.solarHight(latitude * Math.PI / 180, SolarUtil.declination(day) * Math.PI / 180, Math.abs(time - 12) * 15 * Math.PI / 180);
                        double sunAzimuth = SolarUtil.solarAzimuth(sunHeight, latitude * Math.PI / 180, SolarUtil.declination(day) * Math.PI / 180, time - 12);
                        double[][] polygon = null;
                        double shadowX, shadowY;
                        double shadowOfY = Math.abs(highDiff / Math.tan(sunHeight) * Math.cos(sunAzimuth));
                        double shadowOfX = highDiff / Math.tan(sunHeight) * Math.sin(sunAzimuth);
                        if (time > 12) {
                            // Morning situation
                            shadowX = value.getLUPointX() - shadowOfX;
                            shadowY = value.getRDPointY() - shadowOfY;
                            polygon = new double[][]{
                                    {value.getRDPointX(), value.getRDPointY()},
                                    {shadowX + (value.getRDPointX() - value.getLUPointX()), shadowY},
                                    {shadowX, shadowY},
                                    {shadowX, shadowY + (value.getLUPointY() - value.getRDPointY())},
                                    {value.getLUPointX(), value.getRDPointY()},
                                    {value.getRDPointX(), value.getRDPointY()}
                            };
                        } else {
                            // Afternoon situation
                            shadowX = value.getRDPointX() - shadowOfX;
                            shadowY = value.getRDPointY() - shadowOfY;
                            polygon = new double[][]{
                                    {value.getRDPointX(), value.getLUPointY()},
                                    {shadowX, shadowY + (value.getLUPointY() - value.getRDPointY())},
                                    {shadowX, shadowY},
                                    {shadowX - (value.getRDPointX() - value.getLUPointX()), shadowY},
                                    {value.getLUPointX(), value.getRDPointY()},
                                    {value.getRDPointX(), value.getLUPointY()}
                            };

                        }
                        // Is it covered
                        boolean covered = SolarUtil.isCovered(polygon, (building.getRDPointX() + building.getLUPointX()) / 2, (building.getLUPointY() + building.getRDPointY()) / 2);

                        if (time <= sunUp || time >= sunDown) {
                            covered = true;
                        }
                        if (covered) {
                            // Any building cover is a cover
                            total = false;
                            break;
                        }
                    }
                    if (total) {
                        noCoverTime += 0.01;
                    }
                }
                map.put("sunHour", map.get("sunHour") + noCoverTime);

            }
            cubeMap.put(building, map.get("sunHour"));

        }
        return cubeMap;
    }

}

Here, the shadow area of the surrounding buildings is calculated first, and the boundary points are stored in the array to form a polygon. Judge whether the target position is within the polygon area, which means that it is obscured within the shadow range.
Cycle to judge the occlusion of each surrounding building, cycle to calculate the daily light duration in a year, and finally cycle to calculate the annual light duration of each target location. There are a lot of cycles, and the calculation is very computationally expensive. My test case needs about 23s of running time.

6. Testing

package com.dwind.building;

import com.dwind.pojo.Building;
import com.dwind.util.SolarUtil;
import org.junit.jupiter.api.Test;

import java.util.ArrayList;
import java.util.HashMap;

import static org.junit.jupiter.api.Assertions.*;

/**
 * @author lcdwind
 * @date 2021/11/1 9:31
 */
class SunshineTest {

    @Test
    void sunTime() {
        Building target = new Building(10, 5, 0, 0, 5);

        Building building = new Building(20, 2, 5, -5, 10);
        Building building1 = new Building(20, 5, 6, 3, 10);

        ArrayList<Building> buildings = new ArrayList<>();
        buildings.add(building);
        buildings.add(building1);

        double latitude = 34.5;
        double longitude = 113.5;
//        70.9 6108.000000000003 79.9 7524.0 85.9 8267.999999999996

        long start = System.currentTimeMillis();
        Sunshine sunshine = new Sunshine();
        HashMap<Building, Double> map = sunshine.sunTime(target, buildings, latitude,longitude);
        System.out.println(map);
        long end = System.currentTimeMillis();
        System.out.println(end - start);
    }
}

Test results:

{Building{height=10.0, RDPointX=3.0, RDPointY=2.0, LUPointX=2.0, LUPointY=3.0}=2723.4999999999563, Building{height=10.0, RDPointX=4.0, RDPointY=4.0, LUPointX=3.0, LUPointY=5.0}=1665.539999999981, Building{height=10.0, RDPointX=4.0, RDPointY=3.0, LUPointX=3.0, LUPointY=4.0}=2292.6099999999683, Building{height=10.0, RDPointX=5.0, RDPointY=2.0, LUPointX=4.0, LUPointY=3.0}=2907.0799999999567, Building{height=10.0, RDPointX=5.0, RDPointY=3.0, LUPointX=4.0, LUPointY=4.0}=2533.6099999999633, Building{height=10.0, RDPointX=4.0, RDPointY=1.0, LUPointX=3.0, LUPointY=2.0}=3120.6399999999494, Building{height=10.0, RDPointX=5.0, RDPointY=0.0, LUPointX=4.0, LUPointY=1.0}=3385.0299999999424, Building{height=10.0, RDPointX=5.0, RDPointY=4.0, LUPointX=4.0, LUPointY=5.0}=2101.9799999999723, Building{height=10.0, RDPointX=2.0, RDPointY=2.0, LUPointX=1.0, LUPointY=3.0}=2588.4099999999594, Building{height=10.0, RDPointX=2.0, RDPointY=4.0, LUPointX=1.0, LUPointY=5.0}=1172.2899999999863, Building{height=10.0, RDPointX=1.0, RDPointY=1.0, LUPointX=0.0, LUPointY=2.0}=2923.4099999999553, Building{height=10.0, RDPointX=1.0, RDPointY=3.0, LUPointX=0.0, LUPointY=4.0}=1865.1199999999715, Building{height=10.0, RDPointX=2.0, RDPointY=3.0, LUPointX=1.0, LUPointY=4.0}=1956.239999999974, Building{height=10.0, RDPointX=2.0, RDPointY=0.0, LUPointX=1.0, LUPointY=1.0}=3285.299999999948, Building{height=10.0, RDPointX=1.0, RDPointY=2.0, LUPointX=0.0, LUPointY=3.0}=2502.2399999999625, Building{height=10.0, RDPointX=3.0, RDPointY=1.0, LUPointX=2.0, LUPointY=2.0}=3080.9399999999505, Building{height=10.0, RDPointX=5.0, RDPointY=1.0, LUPointX=4.0, LUPointY=2.0}=3174.8799999999483, Building{height=10.0, RDPointX=4.0, RDPointY=2.0, LUPointX=3.0, LUPointY=3.0}=2791.96999999996, Building{height=10.0, RDPointX=3.0, RDPointY=4.0, LUPointX=2.0, LUPointY=5.0}=1539.9799999999827, Building{height=10.0, RDPointX=1.0, RDPointY=0.0, LUPointX=0.0, LUPointY=1.0}=3225.899999999951, Building{height=10.0, RDPointX=3.0, RDPointY=3.0, LUPointX=2.0, LUPointY=4.0}=2182.5799999999695, Building{height=10.0, RDPointX=2.0, RDPointY=1.0, LUPointX=1.0, LUPointY=2.0}=2997.8999999999523, Building{height=10.0, RDPointX=1.0, RDPointY=4.0, LUPointX=0.0, LUPointY=5.0}=1096.6699999999862, Building{height=10.0, RDPointX=3.0, RDPointY=0.0, LUPointX=2.0, LUPointY=1.0}=3339.789999999945, Building{height=10.0, RDPointX=4.0, RDPointY=0.0, LUPointX=3.0, LUPointY=1.0}=3362.059999999947}
20191

summary

It's too slow. I can't finish it

Today is mainly to practice blogging, share and record recent learning.