General idea of the topic
Give you an undirected graph. Each edge in the graph is blue or red. Each time you select a point, you will reverse the color of the edge connected to the point (red turns blue and blue turns red). The scheme of finding the minimum number of steps will make the color of all edges the same.
thinking
I don't think so 2 − s a t 2-sat 2 − sat problem solution, I'll send it.
First, classify and discuss: either all turn red or all turn blue.
If the color of an edge is the same as the current color we expect, either both points are selected or neither is selected. Therefore, if one point is not selected, the other point is not selected. If one point is selected, the other point should also be selected. Just build a map, as shown in the following figure.
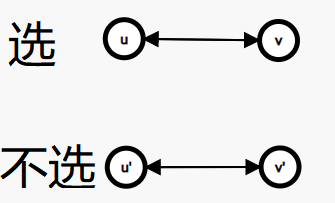
Similarly, if the color of an edge is different from the expected color, so if one point is selected, the other point cannot be selected. If one point is not selected, the other point must be selected. If the figure is omitted.
So we can sort out one 2 − s a t 2-sat 2 − sat model.
Judge the situation without solution, this is 2 − s a t 2-sat 2 − classic operation of sat, judgment u , u ′ u,u' u. Whether u 'is in a strong connected component.
If you have a solution, you have to output the solution. Because the graph is symmetrical up and down, that is, if you choose i 1 , i 2 ... , i m , j 1 ′ , j 2 ′ ... , j m ′ ′ i_1,i_2\dots,i_m,j_1',j_2'\dots,j_{m'}' i1, i2..., im, j1 ′, j2 ′..., jm ′′′, then you must not choose it and choose i 1 ′ , i 2 ′ ... , i m ′ , j 1 , j 2 ... , j m ′ i_1',i_2'\dots,i_m',j_1,j_2\dots,j_{m'} i1 ', i2'..., im ', j1, j2..., jm', so in order to select as few as possible, let's look at the two things u ′ u' Add the number of u 'to the answer, and then put the selected points into the final scheme.
See code for details.
I don't know why there are so many details in other questions. Maybe my method doesn't have any details.
code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
void read(){}//read(a,b,c,..., n);
template<typename _Tp,typename... _Tps>
void read(_Tp &x,_Tps &...Ar){
x=0;char c=getchar();bool flag=0;
while(c<'0'||c>'9')flag|=(c=='-'),c=getchar();
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
if(flag)x=-x;
read(Ar...);
}
const int N=1e5+10;
int n,m;
struct zj{
int u,v,w;
}a[N];
struct edges{
int to,nex;
}edge[N*4];//Note that for each edge, two two-way edges should be built, so the size should be opened four times
int head[N*2],kk;
void addedge(int u,int v){//Chain forward star basic operation, directly build a two-way edge
edge[++kk]=(edges){v,head[u]};head[u]=kk;
edge[++kk]=(edges){u,head[v]};head[v]=kk;
}
int dfn[N*2],low[N*2],s[N*2],top,cnt,scc[N*2],scct;//Don't forget to double the points
void tarjan(int u){//tarjan shrink point template
dfn[u]=low[u]=++cnt;s[++top]=u;
for(int i=head[u];i;i=edge[i].nex){
int v=edge[i].to;
if(!dfn[v])tarjan(v),low[u]=min(low[u],low[v]);
else if(!scc[v])low[u]=min(low[u],low[v]);
}
if(dfn[u]==low[u]){
++scct;
while(s[top]!=u)scc[s[top--]]=scct;
scc[s[top--]]=scct;
}
}
int cnt1,cnt2,k1[N],k2[N],s1[N],s2[N];//Record the number and number of u and u 'arrived in dfs
bool vis[N];
void dfs(int u){
if(vis[(u-1)%n+1])return;//1,2,..., n invariant, n+1,n+2,..., n+n becomes 1,2,..., n
vis[(u-1)%n+1]=1;u<=n?(k1[++cnt1]=u):(k2[++cnt2]=u-n);
for(int i=head[u];i;i=edge[i].nex){
int v=edge[i].to;
dfs(v);
}
}
int get(){
int i;char c[5];bool flag1,flag2;int ans1=0,ans2=0;
for(read(n,m),i=1;i<=m;i++)read(a[i].u,a[i].v),scanf("%s",c),a[i].w=(c[0]=='R');//Proper line pressing can enhance code readability(
for(i=1;i<=m;i++)a[i].w?(addedge(a[i].u,a[i].v),addedge(a[i].u+n,a[i].v+n)):(addedge(a[i].u,a[i].v+n),addedge(a[i].u+n,a[i].v));//That's what I explained above
for(i=1;i<=n*2;i++)if(!dfn[i])tarjan(i);
for(flag1=1,i=1;i<=n;i++)if(scc[i]==scc[i+n])flag1=0;
if(flag1)for(i=1;i<=n;i++){
if(vis[i])continue;
cnt1=cnt2=0;
dfs(i);
if(cnt1<cnt2){//Look at u,u 'choose whichever is less
ans1+=cnt1;
while(cnt1)s1[++s1[0]]=k1[cnt1--];
}
else{
ans1+=cnt2;
while(cnt2)s1[++s1[0]]=k2[cnt2--];
}
//It cannot be written here in order to save code:
//if(cnt1>cnt2)swap(k1,k2),swap(cnt1,cnt2);
//ans1+=cnt1;
//while(cnt1)s1[++s1[0]]=k1[cnt1--];
//This will cause the complexity to become O(n^2) and fly directly to T
}
//-----------------These are all turning blue-----------------
memset(head,0,sizeof(head));kk=0;
memset(dfn,0,sizeof(dfn));cnt=0;
memset(low,0,sizeof(low));
memset(scc,0,sizeof(low));scct=0;
memset(s,0,sizeof(s));top=0;
memset(vis,0,sizeof(vis));
//-----------------Be sure to pay attention to emptying-----------------
for(i=1;i<=m;i++)a[i].w?(addedge(a[i].u+n,a[i].v),addedge(a[i].u,a[i].v+n)):(addedge(a[i].u,a[i].v),addedge(a[i].u+n,a[i].v+n));
for(i=1;i<=n*2;i++)if(!dfn[i])tarjan(i);
for(flag2=1,i=1;i<=n;i++)if(scc[i]==scc[i+n])flag2=0;
if(flag2)for(i=1;i<=n;i++){
cnt1=cnt2=0;
dfs(i);
if(cnt1<cnt2){
ans2+=cnt1;
while(cnt1)s2[++s2[0]]=k1[cnt1--];
}
else{
ans2+=cnt2;
while(cnt2)s2[++s2[0]]=k2[cnt2--];
}
}
//-----------------These are all red-----------------
if(!flag1&&!flag2)return printf("-1"),0;//If there is no solution in both cases, there is no solution
if(!flag1||(flag2&&s1[0]>s2[0]))swap(s1,s2);//If the first case has no solution or the first case is not as good as the second case, choose the second
for(printf("%d\n",s1[0]),i=1;i<=s1[0];i++)printf("%d ",s1[i]);
return 0;//Perfect flower scattering
}
int main(){
return get();//The main function line is mainly used to facilitate multiple groups of test data or switch freopen. Otherwise, it's too troublesome to mark the roller up and comment it out!
}
Warm reminder
If there is any clerical error, comment or private chat with me, I hope I can help you