This paper summarizes some basic operations of chained binary tree in class, including

• Calculate the number of nodes of the binary tree
• Calculate the number of leaf nodes of binary tree
• Calculate the number of nodes in the K-th layer of the binary tree
• Calculate the depth / height of the binary tree
• Find and return the node with the value of x
• Judge whether the binary tree is a complete binary tree
• Destruction of binary tree
• Preorder traversal of binary tree
• Sequence traversal of binary tree

Due to the structural characteristics of binary tree, all the above functions are implemented by recursion, so it is necessary to skillfully use recursion to control binary tree.
The definitions of breadth first traversal and depth first traversal are also mentioned.

Chain structure of binary tree implementation

Structure definition:

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

Manually create a binary tree and put it behind the edge to realize the operation of the binary tree

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	node->data = x;
	node->left = node->right = NULL;
	return node;
}

BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');
	//BTNode* nodeG = BuyNode('G');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	//nodeB->right = nodeG;
	return nodeA;
}

Number of nodes in binary tree

Count with return value
Idea: number of binary tree nodes = number of left subtree nodes + number of right subtree nodes + 1 (root node)

int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

Use counter
Because the local variables in different function stack frames are not the same variable during recursion, it is necessary to count the variables externally and pass its pointer to the function, so that different functions modify the same variable.

//If you want to use a counter, you should bring back the result with parameters
void BinaryTreeSize(BTNode* root, int* pn)
{
	if (root == NULL)
	{
		return;
	}

	++(*pn);
	BinaryTreeSize(root->left, pn);
	BinaryTreeSize(root->right, pn);
}

Number of leaf nodes of binary tree

//Number of leaf nodes of binary tree
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)//The whole tree may be empty, or the subtree may be empty
	{
		return 0;
	}
	//Nodes without left and right children are leaf nodes
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

Number of nodes in the K-th layer of binary tree

Idea: disassemble the problem. The number of nodes in layer K = the number of nodes in layer K-1 of the left subtree + the number of nodes in layer K-1 of the right subtree.

int BinaryTreeLeveKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLeveKSize(root->left, k - 1) + BinaryTreeLeveKSize(root->right, k - 1);
}

Depth / height of binary tree

Idea: binary tree depth = larger value of left subtree depth and right subtree depth + 1 (root node)
Note that in order to avoid repeated calls, the left subtree and right subtree depths need to be saved in variables.

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)//The number of empty tree layers is 0
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

The binary tree looks for a node with a value of x

Requirement: return the node whose value of the first node is equal to x. if it is not found, return NULL
Idea: the empty tree (empty subtree) returns null directly (if the current node is empty, it returns null directly). If the current node is not empty and the value is equal to x, it returns the current node; If the current node value is not equal to x, check whether the left subtree and the right subtree have target nodes.
If the return value is found, it must not be empty. If it is found in the left subtree, it will be returned layer by layer (note that it is not returned to the outermost function in one step), and the right subtree will not be found again.

//The binary tree looks for a node with a value of x
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)//Handle empty trees (or empty subtrees encountered in recursion)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)//If the return value is not empty, it indicates that it is found and returned directly
	{
		return leftRet;
	}
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
	{
		return rightRet;
	}
	return NULL;
}

Judge whether the binary tree is a complete binary tree

The implementation idea of this function is an extension of the following implementation idea of sequence traversal with queue.
When the node is queued, the null pointer is also queued.
When leaving the queue, when a null pointer is encountered, judge whether the remaining elements in the queue are composed of non null nodes. If there are non null nodes, it is not a complete binary tree; On the contrary, it is a complete binary tree.

Note that the queue element type should be changed to the binary tree node pointer type, because I put the declaration of the linked binary tree structure and the queue implementation in different files, so I want to pre declare the binary tree node pointer type.

bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	//Sequence traversal first, and stop when empty (after the complete binary tree encounters empty, the remaining elements behind the queue must be NULL,
	//Incomplete binary trees are not necessarily, and there may be non empty elements that are not in the queue after encountering emptiness)
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);//Null pointers are also queued
			QueuePush(&q, front->right);
		}
	}
	//When empty nodes are encountered, check whether the remaining nodes are non empty
	//1. If the rest is empty, it is a complete binary tree
	//2. If the remaining existence is not empty, it is not a complete binary tree
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);//The headless chain queue has actually released all the space after the pop,
	//However, for users who never know the specific implementation in the queue, logically, space should be released to avoid memory leakage
	return true;
}

Binary tree destruction

Idea: since the root node is released, the child node cannot be found. It must be released from bottom to top. It is suitable for recursive implementation.
Because the first level pointer is passed, the root pointer is externally controlled by the user

void BinaryTreeDestroy(BTNode* root)//Caller null
{
	if (root == NULL)//The empty tree does not have to be empty (or if the subtree is empty, it will directly return to the previous level)
	{
		return;
	}
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}

Traversal of binary tree

Pre order traversal, middle order traversal, post order traversal, sequence traversal, breadth first traversal, depth first traversal

definition:

1. Preorder Traversal (also known as Preorder Traversal) - the operation of accessing the root node occurs before traversing its left and right subtrees.
2. Inorder traversal - the operation of accessing the root node occurs in traversing its left and right subtrees.
3. Postorder traversal -- the operation of accessing the root node occurs after traversing its left and right subtrees.

example:


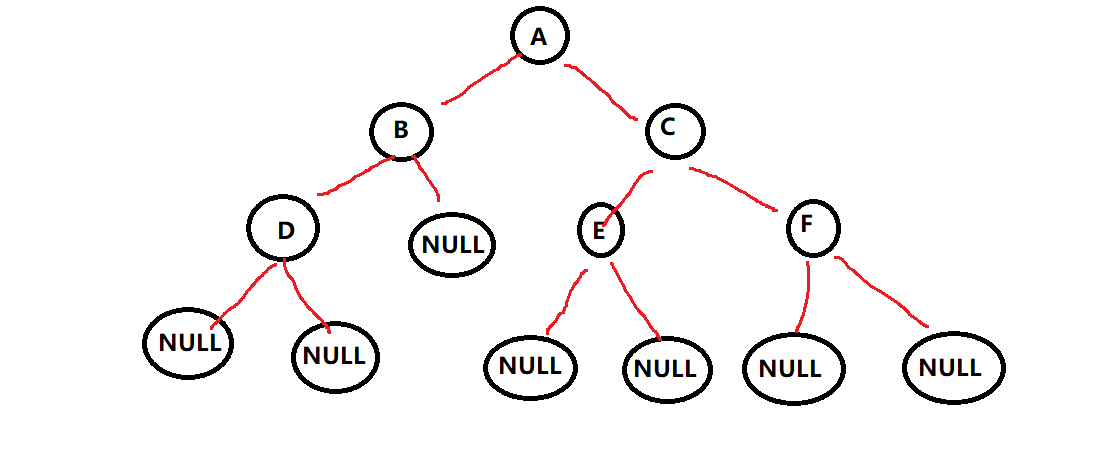
code
Preorder traversal

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

Medium order traversal

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

Postorder traversal

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

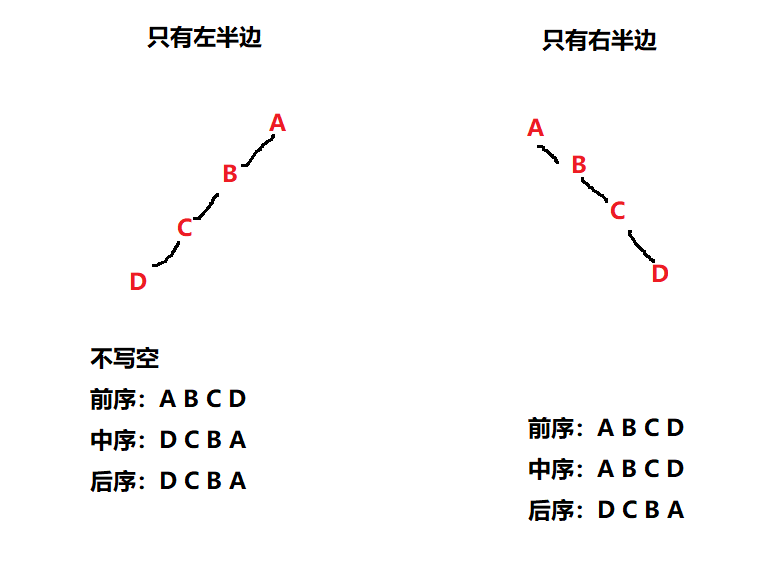
When the access results of current order traversal and post order traversal are exactly the opposite, it indicates that this is a unilateral tree
As shown in the figure:

Sequence traversal definition:
Let the number of layers of the root node of the binary tree be 1. Sequence traversal is to start from the root node of the binary tree, first access the root node of the first layer, then access the nodes on the second layer from left to right, then the nodes on the third layer, and so on. The process of accessing the nodes of the tree layer by layer from top to bottom and from left to right is sequence traversal.
Illustration

Realization idea:
Using queue implementation;
Put the root node into the queue first;
When the queue is not empty, take the first element out of the queue (access this node), and let the two children out of the queue node into the queue (the left child is first), and the null pointer does not enter the queue.
Sequence traversal is implemented when the queue is empty.

code

void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);

		//Bring the children into the queue
		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");

	QueueDestroy(&q);
}

Breadth first traversal definition: traverse all possible positions in the next step before further traversal. Sequence traversal is a breadth first traversal.

Depth first traversal definition: only after traversing a complete path (the complete path from the root to the leaf node) can you turn back to the upper layer, and then traverse the next path. Preorder traversal is a kind of depth first traversal.