For the time being, this blog only deals with the updating of the single update interval of the President Tree, which involves the permanence of the tag.

brief introduction

Before learning the chairman tree, we need to understand the weighted line segment tree.
The weight line segment tree can maintain the number of numbers, and the table below the array maintains the range.
Example:
Question the whole number k (query):
Divide the online segment tree into two parts:
Let's first look at the number of left subtrees. Let's set the number of left subtrees as f.
If f >= t recursively goes into the left subtree to find
If f < K recursively enters the right subtree to find the largest f-k
That is, the whole dichotomy
Above references: Weighted Line Segment Tree
The content is relatively simple and can be learned by oneself.

Presidential tree, also known as persistent line segment tree, is classically used to maintain the value of interval kth.
The chair tree can be dynamic or static. Examples are provided below.
The persistent segment tree should be able to support access to the existing state, so it can not be simply modified on the original node. It is necessary to establish new nodes.
So how many new nodes need to be built?
Obviously, for each single point update, only new leaf nodes need to be created to the root node path, the number of logn, === other nodes can use the previous version of the node. == The implementation will be mentioned in Example 1.
Pictures to help understand (from pengwill97's blog)
The picture shows the new and inherited son node of root 2 after inserting the value 1.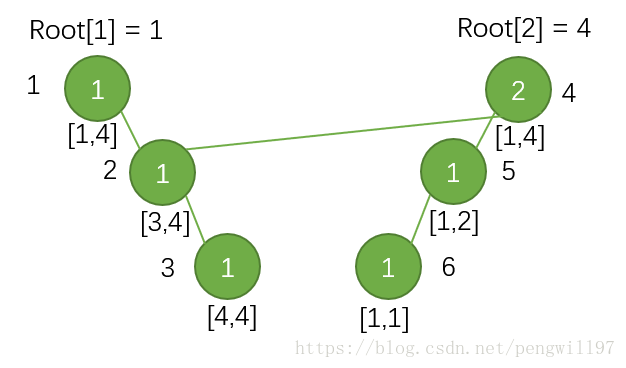

Examples

The code mainly refers to lyd and konjac_tbr

Example 1: Static query interval k is small

Admit that I was confused for a second when I saw this analysis...
Post code

#Include <bits/stdc++.h>// / Question 1, the commentary will be a little more detailed.
using namespace std;
const int MAXN=200001;
struct seg{
    int lc,rc,dat;//lc,rc: pointer to left and right son
}tree[MAXN*20];
int tot,root[MAXN],a[MAXN],n,m,b[MAXN];
int build(int l,int r)
{
    int p=++tot;//New Node
    tree[p].dat=0;
    if(l==r) {return p;}
    int mid=(l+r)>>1;
    tree[p].lc=build(l,mid),tree[p].rc=build(mid+1,r);//Recursive tree building
    return p;//You can also use references here.
}
int insert(int now,int l,int r,int x,int val)//Single point modification
{
    int p=++tot;
    tree[p]=tree[now];
    if(l==r)
    {
        tree[p].dat+=val;return p;
    }
    int mid=(l+r)>>1;
    if(x<=mid) tree[p].lc=insert(tree[now].lc,l,mid,x,val);
    else tree[p].rc=insert(tree[now].rc,mid+1,r,x,val);
    tree[p].dat=tree[tree[p].lc].dat+tree[tree[p].rc].dat;
    return p;
}
int ask(int p,int q,int l,int r,int k){//Interval query k smallest
    if(l==r) return l;//It happens to be the extra k item returned to l
    int mid=(l+r)>>1;
    //How many numbers fall in the range [l,mid]
    int lcnt=tree[tree[p].lc].dat-tree[tree[q].lc].dat;
    if(k<=lcnt) return ask(tree[p].lc,tree[q].lc,l,mid,k);//The difference between the left subtree is enough to be found in the left subtree
    else return ask(tree[p].rc,tree[q].rc,mid+1,r,k-lcnt);//Otherwise, look in the right subtree
}
int main()
{
    scanf("%d%d",&n,&m);int t=0;
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);b[++t]=a[i];
    }
    //Discretization
    sort(b+1,b+t+1);
    t=unique(b+1,b+t+1)-(b+1);
    root[0]=build(1,t);
    for(int i=1;i<=n;++i)
    {
        int x=lower_bound(b+1,b+t+1,a[i])-b;
        root[i]=insert(root[i-1],1,t,x,1);
    }
    for(int i=1;i<=m;++i)
    {
        int l,r,k;scanf("%d%d%d",&l,&r,&k);
        int ans=ask(root[r],root[l-1],1,t,k);//After inserting the number R and the number l-1, the difference between the two is the newly added number in [l,r].
        printf("%d\n",b[ans]);//Retrieve the original value
    }
}

Template: Persistent Segment Tree 1 (Chairman Tree)

Example 2: Dynamic single-point query

#include<bits/stdc++.h>
using namespace std;
#define reg register
#define MAXN 2000001
inline int read(){
    reg char ch=getchar();reg int i=0,f=1;
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f;
}
struct seg{
	int l,r,val;
}tr[MAXN*20];
int n,m,a[MAXN],root[MAXN],cnt;
int build(int l,int r)
{
	int k=++cnt;
	if(l==r)
	{
		tr[cnt].val=a[l];return k;
	}
	int mid=(l+r)>>1;
	tr[k].l=build(l,mid),tr[k].r=build(mid+1,r);
	return k;
}
int change(int now,int l,int r,int x,int val)
{
	int k=++cnt;tr[k]=tr[now];
	if(l==r&&l==x)
	{
		tr[cnt].val=val;return k;
	}
	int mid=(l+r)>>1;
	if(x<=mid) tr[k].l=change(tr[now].l,l,mid,x,val);
	else tr[k].r=change(tr[now].r,mid+1,r,x,val);
	return k;
}
int query(int k,int l,int r,int x)
{
	if(l==r&&l==x) return tr[k].val;
	int mid=(l+r)>>1;
	if(x<=mid) return query(tr[k].l,l,mid,x);
	return query(tr[k].r,mid+1,r,x);
}
int main()
{
	n=read(),m=read();
	for(reg int i=1;i<=n;++i) a[i]=read();
	root[0]=build(1,n);
	for(reg int i=1;i<=m;++i)
	{
		int  version=read(),chk=read();
		if(chk==1)
		{
			int loc=read(),val=read();
			root[i]=change(root[version],1,n,loc,val);//Update the old version
		}
		else if(chk==2){
			int loc=read();
			root[i]=root[version];//Queries also generate new versions
			printf("%d\n",query(root[version],1,n,loc));
		}
	}
}

Template: Persistent Array

Example 3: Persistent and Searchable

Note that persistent and lookup cannot use path compression, so rank-by-rank merging optimization is required.

#include<bits/stdc++.h>
using namespace std;
#define reg register
#define MAXN 200001
inline int read()
{
    reg int x=0,f=1;reg char c=getchar();
    while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
    while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();
    return x*f;
}
struct node{
	int l,r,val;
}tr[MAXN*20];
int n,m,fa[MAXN],root[MAXN<<1],cnt,t,dep[MAXN];
int build(int l,int r)
{
	int p=++cnt;
	if(l==r){
		tr[p].val=fa[l];return p;
	}
	int mid=(l+r)>>1;
	tr[p].l=build(l,mid),tr[p].r=build(mid+1,r);
	return p;
}
int query(int k,int l,int r,int x)
{
	if(l==r) return tr[k].val;
	int mid=(l+r)>>1;
	if(x<=mid) return query(tr[k].l,l,mid,x);
	return query(tr[k].r,mid+1,r,x);
}
int change(int now,int l,int r,int x,int val)
{
	int p=++cnt;tr[p]=tr[now];
	if(l==r)
	{
		tr[p].val=val;return p;
	}
	int mid=(l+r)>>1;
	if(x<=mid) tr[p].l=change(tr[now].l,l,mid,x,val);
	else tr[p].r=change(tr[now].r,mid+1,r,x,val);
	return p;
}
inline int get(int x)
{
	int f=query(root[t],1,n,x);
	if(x!=f) return get(f);
	return x;
}
inline void add(int k,int l,int r,int x)
{
	if(l==r)
	{
		++dep[k];return;
	}
	int mid=(l+r)>>1;
	if(x<=mid) add(tr[k].l,l,mid,x);
	else add(tr[k].r,mid+1,r,x);
}
int main()
{
	n=read(),m=read();
	for(reg int i=1;i<=n;++i) fa[i]=i;
	root[0]=build(1,n);
	for(reg int i=1;i<=m;++i)
	{
		int chk=read();
		if(chk==1)
		{
			int x=read(),y=read();
			int x0=get(x),y0=get(y);
			if(x0!=y0){
				//union by rank
				if(dep[x0]>dep[y0]) swap(x0,y0);
				root[i]=change(root[t],1,n,x0,y0);
				if(dep[x0]==dep[y0]) add(root[i],1,n,y0);//Updating depth
			}
			else root[i]=root[t];
			t=i;
		}
		else if(chk==2){
			t=read();root[i]=root[t];
		}
		else if(chk==3)
		{
			int x=read(),y=read();
			int x0=get(x),y0=get(y);
			root[i]=root[t];
			t=i;
			printf("%d\n",(x0==y0)?1:0);//Trinocular output from konjac_tbr
		}
	}
}```
[Template: Persistent and Searchable](https://www.luogu.org/problemnew/show/P3402)