1. Small summary

Common features of this model:

1. Starting from a node, it is only allowed to go in a specific direction to reach the maximum value of the end point.
2. The problem of upgrading needs to go twice (more k times are the problem of cost flow)

Set partition method
It is divided from all sources of the current state

Small questions when doing questions:

1. Why are data stored from the position of 1 and 1
2. Why initialize the matrix of stored data

Both are for better and more convenient treatment of boundary conditions. The boundary conditions without upper nodes or right nodes can be handled as normal, and the values of those without nodes will not be obtained. For example, in a digital triangle, the initial matrix is initialized to negative infinity. This can not only facilitate processing, but also ensure that the node without the upper left node will not get the false value of the upper left node we added.
How much to initialize depends on the specific situation of the topic. If the values of the nodes in the topic are greater than 0 and the maximum value is calculated, it is OK to initialize to 0. If the value of the node has no range and the maximum value is calculated, it must be initialized to negative infinity. Other attributes should also be considered.

2. Digital triangle

1. Title

Given a digital triangle as shown in the figure below, starting from the top, you can choose to move to the node at the lower left or to the node at the lower right of each node, and go all the way to the bottom. It is required to find a path to maximize the sum of numbers on the path.

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5
 Input format
 The first line contains integers n，Represents the number of layers of a numeric triangle.
next n Rows, each row contains several integers, of which i The second row represents the number triangle i The integer contained in the layer.

Output format
 Output an integer representing the maximum path number and.

Data range
1≤n≤500,
−10000≤Integer in triangle≤10000
 Input example:
5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5
 Output example:
30

2. Analysis

The status represents f[i,j] and represents the maximum value of the sum of numbers from the starting point to all routes on the (i,j) path
Set partition:

1. The status of this node comes from the top left
2. The status of this node comes from the top right

In the specific code, we use g[i][j] to store the value of each node. F [i] [J] represents the maximum value of the sum of numbers on all routes from the starting point to i,j. And f[i][j] how did it come from? Only from the top left or top right. As long as we get the maximum value of the sum of numbers in all routes from the starting point to the upper left node, plus the value of the upper left node, we get the maximum value in all routes from the upper left. Similarly, you can get the maximum value from the node on the right. Take the maximum value of these two values and add the values of node i and J. You get f[i][j].
So there is f[i][j] = max(f[i - 1][j - 1],f[i - 1][j]) + g[i][j];

#include<cstdio>
#include<algorithm>
const int N = 510,INF = - 1e5 + 10;
using namespace std;
int g[N][N],f[N][N];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1; i <= n; i ++)
    {
    	//It is initialized to negative infinity here so that nodes without upper left nodes can be calculated together. In this way, the maximum value is calculated
    	//When there is no upper left node, the node without the upper left node will not choose the upper left node as the answer (because it is negative infinity)
        for(int j = 0; j <= i + 1; j ++)
        {
            f[i][j] = INF;
        }
    }
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= i; j ++)
        {
            scanf("%d",&g[i][j]);
        }
    }
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= i; j ++)
        {
        	//f[i-1][j-1] represents the maximum value of all routes from the starting point to the upper left. Similarly, f[i-1][j] represents the upper right
            f[i][j] = max(f[i - 1][j - 1],f[i - 1][j]) + g[i][j];
        }
    }
    int res =  INF;
    for(int i = 1; i <= n; i ++)
    {
    	//Find the maximum of all results at the bottom
        res = max(res,f[n][i]);
    }
    printf("%d",res);
}

3. Flower picking

1. Title

Hello Kitty I want to pick some peanuts for her favorite Mickey Mouse.
She came to a rectangular peanut field with grid roads(As shown below)，Go in from the northwest corner and out from the southeast corner.
At the intersection of each road in the field, there is a peanut seedling with several peanuts on it. After a peanut seedling, you can pick all the peanuts on it.

Hello Kitty You can only go east or south, not west or North.
ask Hello Kitty How many peanuts can you pick at most.

Input format
 The first line is an integer T，Represents the total number of groups of data.
Next is T Group data.
The first row of each group of data is two integers, representing the number of rows of peanut seedlings respectively R Number of columns C. 
Next for each set of data R Row data, describing peanut seedlings in each row from north to south. Each row of data has C An integer that describes the number of peanuts on each peanut seedling in this row in order from west to East M. 

Output format
 For each group of input data, output a line with the content of Hello Kitty The number of peanuts you can pick the most.

Data range
1≤T≤100,
1≤R,C≤100,
0≤M≤1000
 Input example:
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
 Output example:
8
16

2. Analysis

Similarly, we let f[i][j] represent the maximum number of peanuts for all routes from the starting point to (i,j).
The state represents f[i,j], and represents the maximum value of the sum of all routes from the starting point to (i,j)
Set partition:

1. The status of this node comes from above
2. The status of this node comes from the left

Note that the principle of set division is: no repetition and no leakage
Not all attributes need to be satisfied if they are not repeated. For example, if we calculate the maximum value here, we don't need to meet it. As long as it doesn't affect the calculation of the maximum value, it doesn't matter if they are repeated.

In the code, we also store the data of f in q.
So there is q[i][j] += max(q[i - 1][j],q[i][j - 1])

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
//If the number of peanuts is greater than 0, it can be assigned as 0. When calculating the maximum value, nodes without right or upper nodes will only select their own nodes.
int q[N][N];
int main()
{
    int t;
    cin >> t;
    for(int i = 0; i < t; i ++)
    {
        int r,c;
        cin >> r >> c;
        for(int i = 1; i <= r; i ++)
        {
            for(int j = 1; j <= c; j ++)
            {
                cin >> q[i][j];
                q[i][j] += max(q[i - 1][j],q[i][j - 1]);
            }
        }
        cout << q[r][c] << endl;
    }
}

Generally, linear dp can cycle according to a certain order of subscripts to ensure that the whole is calculated according to the topological cycle. Ensure that when calculating each state, the state on which it depends has been calculated. For example, in this problem, the calculation of the j column node of the i-th layer needs to rely on i-1,j node and i,j -1 node. All calculated before.

4. Minimum toll

1. Title

A businessman walked through a N×N Square grid to participate in a very important business activity.

He wants to go in from the upper left corner of the grid and out from the lower right corner.
It takes 1 unit of time to cross a small square in the middle.
Businessmen must be (2N−1) A unit of time.
When passing through each small square in the middle, you need to pay a certain fee.
The merchant expected to cross out with the least cost within the specified time.
How much does it cost at least?

Note: you can't cross each small square diagonally (that is, you can only move up, down, left, right and can't leave the grid).

Input format
 The first line is an integer that represents the width of the square N. 
behind N Line, each line N A positive integer not greater than 100 is the cost of each small square on the grid.

Output format
 Output an integer indicating the minimum cost required.

Data range
1≤N≤100
 Input example:
5
1  4  6  8  10
2  5  7  15 17
6  8  9  18 20
10 11 12 19 21
20 23 25 29 33
 Output example:
109
 Example explanation
 In the example, the minimum value is 109=1+2+5+7+9+12+19+21+33. 

2. Analysis

The total number of steps in the title cannot exceed 2n-1, which means that you can only go right or down and can't go back.
The status represents f[i,j] and represents the minimum cost of all routes from the starting point to (i,j) path
Set partition:

1. The status of this node comes from above
2. The status of this node comes from the left

In the code, we also store the data of f in q.
So there is q[i][j] += min(q[i - 1][j],q[i][j - 1])

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int q[N][N];

int main()
{
	//Initialize to positive infinity, and perform special processing for the upper and left nodes of 1 and 1 nodes
    memset(q,0x3f,sizeof q);
    q[0][1] = 0;
    q[1][0] = 0;
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= n; j ++)
        {
            cin >> q[i][j];
            q[i][j] += min(q[i - 1][j],q[i][j - 1]);
        }
    }
    cout << q[n][n];
}

5. Grid access

1. Title

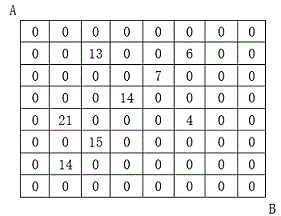
Set N×N In the square graph of, we fill some squares with positive integers, while others put the number 0. As shown in the figure below:
Someone from the top left corner of the picture A Starting, you can walk down or right until you reach the bottom right corner B Point.
On the way, he can take the number in the square (the square will become the number 0).
This person from A Point to B Point walked twice, trying to find two such paths to maximize the sum of the numbers.

Input format
 The first line is an integer N，express N×N A grid of.
The next row has three integers. The first is the number of row numbers, the second is the number of column numbers, and the third is the number placed on the row and column.
Row and column numbers start with 1.
A line of "0" indicates the end.

Output format
 Outputs an integer representing the maximum sum obtained on the two paths.

Data range
N≤10
 Input example:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
 Output example:
67

2. Analysis

Only once:
f[i,j] represents the maximum value of all paths from 1, 1 to i,j
f[i,j] = max(f[i - 1,j] ,f[i,j - 1]) + w[i,j])
Walk twice:
f[i1,j1,i2,j2] represents the maximum value of the path from 1 and 1 to i1,j1 and i2,j2 respectively.
Reduce the dimension of this representation to three dimensions, let's make k = i + j (that is, the sum of the abscissa and ordinate of the grid we are currently walking)
f[k][i1][i2] represents the maximum value of all paths from 1 and 1 to i1,k - i1 and i2,k - i2 respectively

So how to deal with the fact that the same grid cannot be selected repeatedly?
If we define the state as the above four dimensions, we only need to judge i1 == i2 & & j1 = = J2. For the three-dimensional representation, we only need to compare i1 and i2 under the same k (because k is the same, if i1 == i2, then j1 will be equal to j2).
The status represents f[k,i1,i2], and represents the minimum cost of all routes from the starting point (1,1) to (i1,k - i1) and (i2,k - i2)
Set partition:

1. The status of this node is caused by the first time from the top and the second time from the left
2. The status of this node is caused by coming from the top for the first time and from the top for the second time
3. The status of this node is caused by coming from the left for the first time and from the top for the second time
4. The status of this node is caused by the first time from the left and the second time from the left

Calculation of this status value
5. When i1!=i2 means that both nodes are passed only once, the value of this state is w[i1,j1]
6. When i1 == i2 means that two nodes coincide, the value of this state is w[i1,j1]+w[i2,j2]

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 11;
int q[N][N],f[N * 2][N][N];
int main()
{
    int n;
    cin >> n;
    int a ,b ,c;
    while(cin >> a >> b >> c, a || b || c){q[a][b] = c;}
    for(int k = 2; k <= 2 * n; k ++)
    {
        for(int i1 = 1; i1 <= n; i1 ++)
        {
            for(int i2 = 1; i2 <= n; i2 ++)
            {
                if(i1 >= k || i2 >= k) break;
                int j1 = k - i1;
                int j2 = k - i2;
                int t = q[i1][j1];
                //Judge whether the two nodes in the current state coincide
                if(i1 != i2){t += q[i2][j2];}
                int &x = f[k][i1][i2];
                x = max(x,f[k - 1][i1 - 1][i2 - 1] + t);
                x = max(x,f[k - 1][i1 - 1][i2] + t);
                x = max(x,f[k - 1][i1][i2 - 1] + t);
                x = max(x,f[k - 1][i1][i2] + t);
            }
        }
    }
    //Note that the status is defined as f[k][i1][i2]
    cout << f[n + n][n][n];
}

6. Pass a note

1. Title

Obuchi and Xiaoxuan are good friends and classmates. They always have endless topics together.
In a quality development activity, the students in the class arranged to sit together m that 's ok n Column matrix, and Obuchi and Xiaoxuan are arranged at both ends of the diagonal of the matrix, so they can't talk directly.
Fortunately, they can communicate by passing notes.
The note had to be passed to the other party through many students. Obuchi sat in the upper left corner of the matrix with the coordinates (1,1)，Xiaoxuan sits in the lower right corner of the matrix with coordinates (m,n). 
The note from Xiaoyuan to Xiaoxuan can only be passed down or right, and the note from Xiaoxuan to Xiaoyuan can only be passed up or left. 
During the activity, Obuchi hopes to pass a note to Xiaoxuan and hope Xiaoxuan will reply to him.
Each student in the class can help them pass, but will only help them once, that is, if this person helps when Xiaoxuan hands Xiaoxuan a note, he will not help when Xiaoxuan hands it to Xiaoyuan, and vice versa. 
Another thing to note is that each student in the class is willing to help with varying degrees of favor (Note: the degree of kindness of Obuchi and Xiaoxuan is not defined, and it is expressed as 0 when entering). You can use a 0∼100 The larger the number, the better.
Obuchi and Xiaoxuan hope to find students with a high degree of kindness to help pass the note, that is, to find two transmission paths back and forth, so as to maximize the sum of the kindness of the students on these two paths.
Now, please help Obuchi and Xiaoxuan find these two paths.

Input format
 The first line has 2 integers separated by spaces m and n，Indicates that the student matrix has m that 's ok n Columns.

Next m Line is a m×n Matrix, the second in the matrix i that 's ok j The integer of the column represents sitting at i that 's ok j The degree of kindness of the students in each row n Integers are separated by spaces.

Output format
 Output an integer indicating the maximum value of the sum of the kindness of the students involved in passing the note on the two roads back and forth.

Data range
1≤n,m≤50
 Input example:
3 3
0 3 9
2 8 5
5 7 0
 Output example:
34

2. Analysis

This question is as like as two peas.
"Once you help, you won't help again" means that when you go to the same node twice, the enthusiasm for the second time is 0
The route from Xiaoyuan to Xiaoxuan is actually equivalent to that from Xiaoxuan to Xiaoyuan. The route from Xiaoxuan to Xiaoyuan can also be regarded as the route from Xiaoyuan to Xiaoxuan again.
So as like as two peas, the boundary conditions are changed.
Therefore, it still needs to be considered to convert the topic into a topic that has been done before.

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 60;
int q[N][N],f[N * 2][N][N];
int main()
{
    int n,m;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m; j ++)
        {
            cin >> q[i][j];
        }
    }
    
    for(int k = 2; k <= m + n; k ++)
    {
        for(int i1 = 1; i1 < k; i1 ++)
        {
            for(int i2 = 1; i2 < k; i2 ++)
            {
                int j1 = k - i1;
                int j2 = k - i2;
                int t = q[i1][j1];
                if(i1 != i2) t += q[i2][j2];
                int &x = f[k][i1][i2];
                x = max(x,f[k - 1][i1 - 1][i2 - 1] + t);
                x = max(x,f[k - 1][i1 - 1][i2] + t);
                x = max(x,f[k - 1][i1][i2 - 1] + t);
                x = max(x,f[k - 1][i1][i2] + t);
            }
        }
    }
    cout << f[m + n][n][n];
}

reference material

Acwing algorithm improvement course