Chapter 1 of "graph theory" and check the class to pass
A. [example 1] [template] and search set
subject
code
#include <iostream>
#include <cstdio>
#define nn 10010
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int n , m;
int fa[nn];
int findroot(int x) {
return fa[x] == x ? fa[x] : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
if(findroot(x) != findroot(y))
fa[findroot(x)] = findroot(y);
}
int main() {
n = read() , m = read();
for(int i = 1 ; i <= n ; i++)
fa[i] = i;
for(int i = 1 ; i <= m ; i++) {
int ty , x , y;
ty = read() , x = read() , y = read();
if(ty == 1)
uni(x , y);
else
puts(findroot(x) == findroot(y) ? "Y" : "N");
}
return 0;
}
B. [example 2] automatic program analysis
subject
code
#include <iostream>
#include <cstdio>
#include <cstring>
#define nn 1000010
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int head[nn] , nxt[nn] , dat[nn];
const int mod = 100007;
int find(int x) {
static int cnt = 0;
for(int i = head[x % mod] ; i ; i = nxt[i]) {
if(dat[i] == x)
return i;
}
++cnt;
nxt[cnt] = head[x % mod] , dat[cnt] = x , head[x % mod] = cnt;
return cnt;
}
int fa[nn];
int findroot(int x) {
return fa[x] == x ? fa[x] : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
if(findroot(x) != findroot(y))
fa[findroot(x)] = findroot(y);
}
int n , m;
int neq[nn][2];
int main() {
int T = read();
while(T--) {
memset(head , 0 , sizeof(head));
memset(nxt , 0 , sizeof(nxt));
memset(dat , 0 , sizeof(dat));
m = 0;
n = read();
for(int i = 1 ; i <= nn - 1 ; i++)
fa[i] = i;
for(int i = 1 ; i <= n ; i++) {
int x = find(read()) , y = find(read());
if(read() == 1)
uni(x , y);
else {
++m;
neq[m][0] = x;
neq[m][1] = y;
}
}
bool res = true;
for(int i = 1 ; i <= m ; i++) {
if(findroot(neq[i][0]) == findroot(neq[i][1])) {
res = false;
break;
}
}
puts(res ? "YES" : "NO");
}
return 0;
}
C. [example 3] legend of Galaxy Heroes
subject
Topic background
In 5801, the earth's inhabitants moved to Taurus α \alpha α The second planet, where the declaration of the founding of the Galactic Federation was issued, changed to the cosmic calendar year in the same year, and began to expand into the depths of the Milky way.
In 799, the two major military groups in the galaxy broke out in the bamilien domain. Taishan Yading group sent space fleet commander Reinhart to lead more than 100000 warships to fight, and Yang Weili, a named General of the group, organized 30000 warships under his command to meet the enemy.
Title Description
Yang Weili is good at arranging troops and arrays, skillfully uses various tactics, and repeatedly defeats more with less, which inevitably leads to arrogance. In this decisive battle, he divided the battlefield of bamilien into 30000 30000 30000 columns, each numbered 1 , 2 , ... , 30000 1,2,...,30000 1,2,…,30000. After that, he numbered his warships as 1 , 2 , ... , 30000 1,2,...,30000 1,2,..., 30000, let the first i i Warship i is in position No i i Column i, forming a "one word long snake array" to lure the enemy in-depth. This is the initial formation. When the invading enemy arrives, Yang Weili will issue merger instructions many times to concentrate most of the warships on a certain column and carry out intensive attacks. The merger instruction is M i j, which has the meaning of i i The entire battleship queue where warship i is located is connected as a whole (head in front and tail in rear) to the third j j The tail of the battleship queue where warship j is located. Obviously, the warship queue is composed of one or more warships in the same column. The execution result of the merge instruction will increase the queue.
However, the wily Reinhart has already taken the initiative in strategy. During the war, he can monitor Yang Weili's fleet mobilization instructions at any time through a huge intelligence network.
While Yang Weili issued instructions to mobilize the fleet, Reinhart also issued some inquiry instructions: C i j in order to timely understand the current distribution of Yang Weili's warships. The instruction means that the computer asks Willie Yang i i Warship i and No j j Whether warship j is currently in the same column, and if so, how many warships are arranged between them.
As a senior programmer, you are required to write programs to analyze Yang Weili's instructions and answer Reinhart's questions.
Input format
The first line has an integer T T T( 1 ≤ T ≤ 5 × 1 0 5 1 \le T \le 5 \times 10^5 1≤T≤5 × A total of 105) T T T instructions.
Here are T T Line T, with one instruction per line. The instruction has two formats:
- M i j: i i i and j j j is two integers( 1 ≤ i , j ≤ 30000 1≤i,j≤30000 1 ≤ i,j ≤ 30000), indicating the warship number involved in the instruction. The order is a fleet transfer order issued by Yang Weili overheard by Reinhardt, and the second party is guaranteed i i Warship i and No j j Warship j is not in the same column.
- C i j: i i i and j j j is two integers( 1 ≤ i , j ≤ 30000 1≤i,j≤30000 1 ≤ i,j ≤ 30000), indicating the warship number involved in the instruction. This instruction is an inquiry instruction issued by Reinhart.
Output format
Analyze and process each input instruction in turn:
- If it is the fleet transfer order issued by Yang Weili, it indicates that the fleet arrangement has changed. Your program should pay attention to this, but do not output any information.
- If it is a query instruction issued by Reinhart, your program will output a line containing only an integer, which is expressed in the same column, the second line i i Warship i and No j j Number of warships arranged between warships j. If the first i i Warship i and No j j If warship j is not in the same column, then - 1 is output.
Sample input and output
Enter #1
4 M 2 3 C 1 2 M 2 4 C 4 2
Output #1
-1 1
Description / tips
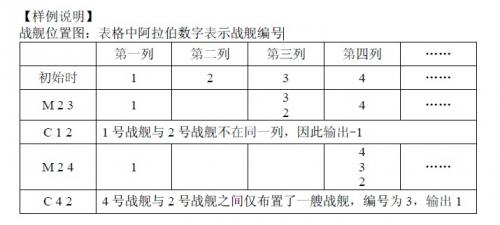
Warship location map: Arabic numerals in the table indicate the warship number
thinking
First, I make complaints about it. I wrote it out with a positive solution. A violent thing should be written for so long.
The original idea
Directly use the chain + parallel search set to judge whether the two warships are in the same queue. Each query can be touched down the chain, which is time complexity O ( n 2 ) O(n^2) O(n2) seems to pass
Primary optimization
record f r o n t i front_i fronti, meet the warship f r o n t i front_i fronti i i In front of i, record v a l i val_i vali , indicates f r o n t i front_i fronti and i i I (excluding i i i) How many warships are there between, s i z i siz_i sizi , denotes i i i number of fleets headed (if any) i i i is not at the head of the team, then s i z i siz_i sizi (meaningless), maintain it every time, and jump one level at a time when asking. The worst complexity is O ( n 2 ) O(n^2) O(n2)
Quadratic optimization
We maintain it regularly f r o n t i front_i fronti and v a l i val_i vali, that is, if the current chain is too long, we directly let f r o n t i front_i fronti points to the first warship of the current fleet, colleagues update v a l val val.
So when do we maintain it? According to the idea of block / Mo team (it doesn't matter if we don't learn), if the length of the chain l e n i len_i leni # over n \sqrt n n , we'll check all the warships f r o n t front front and v a l val Maintenance of val In this way, the length of the chain basically does not exceed n \sqrt n n , the number of inquiries is n n n. Then the time of inquiry is O ( n n ) O(n\sqrt n) O(nn ); The complexity of maintenance is O ( n ) O(n) O (n) (each point can be traversed twice at most, and the constant is ignored), at most n \sqrt n n The complexity of maintenance is O ( n n ) O(n\sqrt n) O(nn )
To sum up, the time complexity is O ( n n ) O(n\sqrt n) O(nn )
Final optimization
Close complexity O ( n ) O(n) O(n), you can rush to the first page of the valley optimal solution
According to the above ideas, why don't we put v a l val Is val's update integrated into the path compression of parallel search set? That is, the path is compressed and the update is completed at the same time
More specifically, combined with code analysis
code
Quadratic optimization
#include <iostream>
#include <cstdio>
#define nn 300010
//#pragma GCC optimize(2)
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int head[nn] , end[nn];
int nxt[nn] , id[nn];
int front[nn];
void insert(int x , int y) {
static int cnt = 0;
++cnt;
if(head[x] == 0) head[x] = end[x] = cnt;
else nxt[end[x]] = head[y];
id[cnt] = y , end[x] = end[y];
}
int n = 30000;
int fa[nn];
int siz[nn];
int val[nn];
int len[nn];
int findroot(int x) {
return fa[x] == x ? fa[x] : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
if(findroot(x) != findroot(y))
fa[findroot(x)] = findroot(y);
}
int cnt1 , cnt2;
int getans(int x) {
int sum = 0;
int cnt = 0;
do {
sum += val[x];
x = front[x];
++cnt;
++cnt1;
}while(front[x] != x);
return sum;
}
int abs_(int x) {return x < 0 ? -x : x;}
int main() {
for(int i = 1 ; i <= n ; i++)
fa[i] = i , siz[i] = 1 , val[i] = 0 , front[i] = i , len[i] = 1 , insert(i , i);
int T = read();
while(T--) {
char ty = getchar();
while(ty != 'M' && ty != 'C') ty = getchar();
int u = read() , v = read();
if(ty == 'M') {
u = findroot(u) , v = findroot(v);
insert(v , u);
front[u] = v;
fa[u] = v;
val[u] = siz[v] , siz[v] += siz[u] , len[v] += len[u];
if(len[v] * len[v] >= n) {
for(int j = 1 ; j <= n ; j++)
if(fa[j] == j) {
len[j] = 1;
int v = 0;
for(int i = head[j] ; i ; i = nxt[i])
val[id[i]] = v++ , front[id[i]] = j , ++cnt2;
}
}
}
else {
if(findroot(u) != findroot(v))
puts("-1");
else {
printf("%d\n" , abs_(getans(u) - getans(v)) - 1);
}
}
}
return 0;
}
Final optimization
#include <iostream>
#include <cstdio>
#define nn 300010
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int n = 30000;
int val[nn];//How many warships are there from I to fa[i] (including i)
int siz[nn];
int prefaval[nn];//pre_FatherValue The weight of the previous / parent node. Note: it is not the weight of the previous / parent node
int fa[nn];
int findroot(int x) {
if(fa[x] == x) return x;
int prefa = fa[x];
fa[x] = findroot(fa[x]);//Path compression
val[x] += val[prefa] - prefaval[x];//It should be understood that val[prefa] is the updated value, while fa[x] changes, and the number of warships between X and prefa remains the same
prefaval[x] = val[fa[x]];
return fa[x];
}
inline int abs_(int x) {return x < 0 ? -x : x;}
int main() {
for(int i = 1 ; i <= n ; i++)
fa[i] = i , val[i] = 1 , siz[i] = 1;//Note initialization
int T = read();
for(int i = 1 ; i <= T ; i++) {
char ty = getchar();
while(ty != 'M' && ty != 'C') ty = getchar();
int u = read() , v = read();
if(ty == 'M') {
u = findroot(u);
v = findroot(v);
fa[u] = v;
val[u] += siz[v];
siz[v] += siz[u];
prefaval[u] = val[fa[u]];
}
else {
if(findroot(u) != findroot(v))//Check whether they are in the same fleet and update val by the way
puts("-1");
else
printf("%d\n" , abs_(val[u] - val[v]) - 1);
}
}
return 0;
}
D. [example 4] food chain
subject
Title Description
There are three kinds of animals a, B and C in the animal kingdom. The food chains of these three kinds of animals form an interesting ring. A eats B, B eats C, and C eats a.
There are N animals, numbered with 1-N. Every animal is one of a, B and C, but we don't know which one it is.
There are two ways to describe the food chain relationship formed by these N animals:
- The first statement is 1 X Y, which means that X and Y are of the same kind.
- The second is 2 X Y, which means X eats Y.
The man used the above two statements to say K sentences to N animals one by one. Some of these K sentences are true and some are false. When a sentence satisfies one of the following three points, it is a lie, otherwise it is the truth.
- The current words conflict with some of the previous true words, which is a lie
- In the current words, X or Y is larger than N, which is a lie
- The current words mean that X eats X, which is a lie
Your task is to output the total number of lies according to the given N and K sentences.
Input format
Two integers in the first line, N and K, indicate that there are n animals and K sentences.
One sentence at the beginning of the second line (see the sample according to the requirements of the topic)
Output format
A line, an integer, represents the total number of lies.
Sample input and output
Enter #1
100 7 1 101 1 2 1 2 2 2 3 2 3 3 1 1 3 2 3 1 1 5 5
Output #1
3
Description / tips
1 ≤ N ≤ 5 ∗ 10^4
1 ≤ K ≤ 10^5
About category and search set (be sure to read it first)
First put a question (for the template question of category and search set, it is recommended to do it first, and it won't take much time, otherwise you won't understand the "food chain"):
Template question
thinking
It's very simple. I like greed and I like the two-point answer. The question is how do we judge whether two criminals are in / not in the same prison
Ordinary parallel search can solve the relationship between friends, but it is not enough for the relationship between enemies: "the enemy of the enemy is my friend". How to deal with this?
Therefore, the category and search set are on the stage:
I think this picture can well describe the types and search the collection:

Tell the following story:
The world is composed of two parts. We call it world one and world two. Everything has its opposite. In order to maintain balance, if i i i is the anode in world one, then i i i is the cathode in world 2, on the contrary, if i i i is the cathode in world one, so i i i is the anode in world two Further, if i i i and j j j is the opposite in the same world, then the number one world i i i and world two j j j is the same kind, the second world i i i and world one j j j is of the same kind
Is that enough
1, World two is two parallel search sets, so we can judge
i
i
i and
j
j
j's hostile relationship
We extend the search set to
2
n
2n
2n, subscript 1$n $is "world one", $n$+1
2
n
2n
2n is "world two"
Complete code
#include <iostream>
#include <cstdio>
using namespace std;
#define N 20010
#define M 100010
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int n , m;
int fa[N * 2];
int x[M] , y[M] , c[M] , maxc;
int findroot(int x) {
return fa[x] == x ? x : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
if(findroot(x) != findroot(y))
fa[findroot(x)] = findroot(y);
}
bool check(int C) {
for(int i = 1 ; i <= n ; i++)
fa[i] = i , fa[i + n] = i + n;
for(int i = 1 ; i <= m ; i++) {
if(c[i] > C) {
if(findroot(x[i]) == findroot(y[i]) || findroot(x[i] + n) == findroot(y[i] + n))//If x [i] and Y [i] are in the same prison
return false;
uni(x[i] + n , y[i]);//Make sure x [i] and Y [i] are not in the same prison
uni(x[i] , y[i] + n);
}
}
return true;
}
int main() {
n = read() , m = read();
for(int i = 1 ; i <= m ; i++)
x[i] = read() , y[i] = read() , maxc = ((c[i] = read()) > maxc ? c[i] : maxc) ;
int l = 0 , r = maxc;
while(l < r) {
int mid = (l + r) / 2;
if(check(mid))
r = mid;
else
l = mid + 1;
}
cout << l;
return 0;
}
Idea of this topic
Similar to the above question, expand the parallel search set to 3 n 3n 3n, for a x x x, x x x eat x + n x+n x+n, x + n x+n x+n eat x + 2 n x+2n x+2n, x + 2 n x+2n x+2n eat x x x
For similar cases, Direct Consolidation:
uni(x , y); uni(x + n , y + n); uni(x + 2 * n , y + 2 * n);
about x x x eat y y Case of y:
Have the following relationship
a
→
b
a\to b
Table a → b
a
a
a eat
b
b
b :
{
x
→
y
x
→
x
+
n
x
+
n
→
x
+
2
n
x
+
2
n
→
x
y
→
y
+
n
y
+
n
→
y
+
2
n
y
+
2
n
→
y
\begin{cases} x&\to y\\ x&\to x+n\\ x+n&\to x+2n\\ x+2n&\to x\\ y&\to y+n\\ y+n&\to y+2n\\ y+2n&\to y \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧xxx+nx+2nyy+ny+2n→y→x+n→x+2n→x→y+n→y+2n→y
The following similar relationships can be obtained:
uni(x , y + 2 * n); uni(x + 2 * n , y + n); uni(y , x + n);
For judging the conflict, I understand it and refer to the code
code
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 50010
#define LIE {++ans;continue;}
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int n , k;
int fa[N * 3];
int ans;
int findroot(int x) {
return fa[x] == x ? x : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
fa[findroot(x)] = findroot(y);
}
int main() {
n = read() , k = read();
for(int i = 1 ; i <= n * 3 ; i++)
fa[i] = i;
for(int i = 1 ; i <= k ; i++) {
int ty = read() , x = read() , y = read();
if(x > n || y > n) LIE
if(findroot(x) == findroot(y)) {
if(ty != 1)
++ans;
continue;
}
if(ty == 1) {
if(findroot(x + n) == findroot(y) || findroot(x) == findroot(y + n))
LIE
uni(x , y);
uni(x + n , y + n);
uni(x + 2 * n , y + 2 * n);
}
else {
if(findroot(x) == findroot(y) || findroot(x) == findroot(y + n))
LIE
uni(x , y + 2 * n);
uni(x + 2 * n , y + n);
uni(y , x + n);
}
}
cout << ans;
return 0;
}
E. [example 5] supermarket shopping
This question is the same as Chapter 1 of "data structure" - binary stack class clearance - [example 4] work arrangement, Luogu[ USACO09OPEN]Work Scheduling G As like as two peas
Skip
subject
thinking
Greed + big root pile
We sort the work deadline from large to small, and set the current time as d i d_i di (note that at this time, the i i i work has been closed), and the deadline is d i d_i All of di's work is put into the pile and set j < i j<i J < I and d j ≠ d i d_j\neq d_i dj=di, j j j takes the maximum value. If the heap is not empty, we take it out of the heap d j − d i d_j-d_i dj − di − work, put their P P P is added to the answer
Just output the answer
code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define nn 100010
#define ll long long
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
struct Heap {
int siz;
int a[nn * 2] , b[nn * 2];
bool ty;
inline void swap_(int x , int y) {
int tmp;
tmp = a[x] ; a[x] = a[y] ; a[y] = tmp;
tmp = b[x] ; b[x] = b[y] ; b[y] = tmp;
}
void clear() {
siz = 0 , ty = 0;
memset(a , 0 , sizeof(a));
}
inline void push(int dat , int dat2) {
a[++siz] = dat;
b[siz] = dat2;
int p = siz;
while(p > 1 && (!(a[p >> 1] < a[p]) ^ ty))
swap_(p >> 1 , p) , p >>= 1;
}
inline void pop() {
swap_(1 , siz);
--siz;
int p = 1 , tmp;
while(p * 2 <= siz && (!(a[p] < a[tmp = ( p * 2 + 1 > siz ? p * 2 : (a[p * 2] < a[p * 2 + 1] ^ ty ? p * 2 : p * 2 + 1) ) ] ) ^ ty))
swap_(tmp , p) , p = tmp;
}
inline int top() {
return siz == 0 ? 0 : a[1];
}
inline bool empty() {
return siz == 0;
}
} h;
struct node {
int d , p;
} wk[nn];
bool cmp(node a , node b) {
return a.d > b.d;
};
int n;
signed main() {
// freopen("P2949_2.in" , "r" , stdin);
h.clear();
h.ty = 1;
n = read();
for(int i = 1 ; i <= n ; i++)
wk[i].d = read() , wk[i].p = read();
++n;
wk[n].d = wk[n].p = 0;
sort(wk + 1 , wk + n + 1 , cmp);
ll ans = 0;
h.push(wk[1].p , wk[1].d);
int i;
for(i = 2 ; i <= n && wk[i].d == wk[i - 1].d ; i++)
h.push(wk[i].p , wk[i].d);
while(i <= n) {
int num = wk[i - 1].d - wk[i].d;
while(num-- && !h.empty()) {
ans += (ll)h.top();
h.pop();
}
h.push(wk[i].p , wk[i].d);
for(++i ; i <= n && wk[i].d == wk[i - 1].d ; i++)
h.push(wk[i].p , wk[i].d);
}
cout << ans;
return 0;
}
F. [example 6] break one by one
subject
Topic background
On the Pingjin battlefield of the three major campaigns, Fu Zuoyi group set up a long snake array on the railway line from Tangshan in the east to Zhangjiakou in the west, centered on Peiping and Tianjin, and tried to escape from the sea to the South or to the west when it was defeated. In order to annihilate the enemy on the spot and prevent him from escaping, Grandpa Mao formulated the strategic policy of cutting off the retreat of the enemy at both ends of the East and West, and then annihilating the enemy one by one. Adhering to the strategic thinking of great military strategists, as a wise commander, you have encountered a similar battlefield situation.
Title Description
Now there are n cities, K of which are occupied by enemy legions. N cities are connected by N-1 roads. The cost of destroying one of the roads is known. Now, tell you the cities where k enemy legions are located and the cost of destroying all roads. Please calculate the minimum cost and separate the K local legions from each other, so as to defeat the enemy one by one in the second step.
Input format
The first line of k contains two positive integers.
The second line contains k integers, indicating which city is occupied by the enemy.
The next n-1 line contains three positive integers a, b and c, indicating that there is a highway from city a to city b and the cost of damage c. The city number starts at 0.
Output format
Output an integer per line, indicating the least cost.
Sample input and output
Enter #1
5 3 1 2 4 1 0 4 1 3 8 2 1 1 2 4 3
Output #1
4
Description / tips
[data range]
10% data: 2 ≤ n ≤ 10;
100% data: 2 ≤ n ≤ 100000, 2 ≤ k ≤ n, 1 ≤ c ≤ 1000000.
thinking
Sort each edge according to the edge weight from large to small, and traverse it in turn. If one edge is connected x x x, y y y. Weight is v a l val val, if x x x and y y y are connected to the occupied cities and x x x, y y The occupied cities connected by y are not the same city. Skip. Otherwise, add this edge to the graph * * (there is no edge at the beginning of the graph)**
In this way, the occupied cities are separated from each other and the sum of deleted edge weights is minimized
How to judge x x Is x connected to the occupied city? It's very simple. Just force the occupied city to be the root when merging, that is, findroot(x) is the same as x x x connected occupied cities
code
#include <iostream>
#include <cstdio>
#include <algorithm>
#define N 100010
#define M 500010
#define int long long
using namespace std;
int read() {
int re = 0;
char c = getchar();
bool sig = true;
while(c < '0' || c > '9') {
if(c == '-') sig = false;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return sig ? re : -re;
}
struct node{
int x , y , val;
}edge[M];
bool cmp(node a , node b) {
return a.val > b.val;
}
int fa[N];
int occ[N];//occupy Occupied
int findroot(int x) {
return fa[x] == x ? x : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
if(findroot(x) != findroot(y)) {
if(occ[y])
fa[findroot(x)] = fa[y];
else
fa[findroot(y)] = fa[findroot(x)];
}
}
int n , m , k;
int ans , sum;
signed main() {
n = read() , m = read() , k = read();
for(int i = 1 ; i <= n ; i++)
fa[i] = i;
for(int i = 1 ; i <= k ; i++)
occ[read() + 1] = true;
for(int i = 1 ; i <= m ; i++)
edge[i].x = read() + 1 , edge[i].y = read() + 1 , sum += (edge[i].val = read());
sort(edge + 1 , edge + m + 1 , cmp);
for(int i = 1 ; i <= m ; i++) {
int x = edge[i].x , y = edge[i].y , u , v;
u = findroot(x) , v = findroot(y);
if(occ[u] && occ[v] && u != v)
continue;
uni(u , v);
ans += edge[i].val;
}
cout << sum - ans;
return 0;
}