Chapter 3 linear table
Definition of linear table
Linear List: a finite sequence of zero or more data elements.
Emphasis: first, it is a sequence. Then emphasize that the linear table is limited.
(direct) precursor element, (direct) successor element.
The number of linear table elements n(n ≥ 0) is defined as the length of the linear table. When n=0, it is called an empty table.
Abstract data type of linear table
ADT Linear table(List)
Data
A collection of data objects for a linear table{a1,a2,a3,......,an},The type of each element is Datatype. Among them,
Except for the first element a1 In addition, each element has and has only one direct precursor element, except the last element an Outside,
Each element has only one direct successor element. The relationship between data elements is one-to-one.
Operation
InitList(*L): Initialize the operation and create an empty linear table L.
ListEmpty(L): Return if linear table is empty true,Otherwise return false.
ClearList(*L): Empty the linear table.
GetElem(L,i*e): Linear table L pass the civil examinations i Location elements returned to e.
LocateElem(L,e): In linear table L Find and given values in e Equal elements. If the equal search is successful,
Returns the serial number of the element in the table, indicating success; Otherwise, 0 means failure.
ListInsert(*L,i,e): In linear table L Section in i Insert a new element at a location e.
ListDelete(*L,i,*e):Delete linear table L pass the civil examinations i A location element and e Returns its value.
ListLength(L): Return linear table L Number of elements.
endADT
Sequential storage structure of linear table
Sequential storage definition
The sequential storage structure of linear table refers to the sequential storage of data elements of linear table with a section of storage units with continuous addresses.
Sequential storage mode
Generally, a one bit array is used to realize the sequential storage structure. The first data element is stored in the position where the index of the array is 0, and then the adjacent elements of the linear table are stored in the adjacent position of the array.
Sequential storage code of linear table:
#define MAXSIZE 20 // Initial allocation of storage space
typedef int ElemType; // The type of ElemType depends on the actual situation. Here, it is assumed to be int
typedef struct {
ElemType data[MAXSIZE]; // The array stores data elements, and the maximum value is MAXSIZE
int length; // Current length of linear table
}SqList;
Here, we find that three attributes are required to describe the sequential storage structure:
- The starting position of storage space: array data. Its storage position is the storage space of storage space.
- Maximum storage capacity of linear table: array length MaxSize.
- Current length of linear table: length.
Difference between data length and linear table length
The length of a linear table is the number of data elements in the linear table. (linear table length ≤ array length).
Address calculation method
The ith element of the linear table is to be stored at the position of the array subscript i-1.
Storing a sequential table with an array means allocating a fixed length of array space. Because the linear table can be inserted and deleted, the allocated array space should be greater than or equal to the length of the current linear table.
Each storage unit in the memory has its own number, which is called the address.
Insertion and deletion of sequential storage structure
Get element operation (GetElem)
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
// Status is the type of function, and its value is the status code of the result of the function, such as OK
// Initial recognition condition: sequential linear table l already exists, 1 ≤ i ≤ ListLength(L)
// Operation result: use e to return the value of the ith data element in L.
Status GetElem(SqList L, int i, ElemType *e) {
if (L.length == 0 || i < 1 || i > L.length)
return ERROR;
*e = L.data[i - 1];
return OK;
}
Note: the return value type here is Status, which is an integer, and the return OK represents 1 and ERROR represents 0. After that, it appears in the code, which is not explained in detail.
Insert operation (ListInsert)
Insert algorithm idea:
- If the insertion position is unreasonable, an exception is thrown;
- If the length of the linear table is greater than or equal to the length of the array, throw an exception or dynamically increase the capacity.
- Traverse forward from the last element to the i-th position, and move them back one position respectively.
- Fill in the element to be inserted at position i
- Table length plus one
Status ListInsert(SqList *L, int i, ElemType e) {
int k;
if (L->length == MAXSIZE) //Linear table full
return ERROR;
if (i < 1 || i > L->length) //i do not meet the scope
return ERROR;
if (i <= L->length) { //Insert footer of data
for (k = L->length - 1; k >= i - 1; k--) {
L->data[k + 1] = L->data[k];//Move one bit to the right from the last one
}
}
L->data[i - 1] = e; //Insert new element
L->length++;
return OK;
}
Delete operation
Ideas for deletion:
- If the deletion position is unreasonable, an exception is thrown.
- Remove and delete elements.
- Traverse from the deleted element position to the last element position, and move them forward one position respectively;
- Subtract one from the length of the watch.
code implementation
//Delete element
//Initial condition: linear table l already exists, 1 ≤ i ≤ ListLength(L)
//Operation result: delete the ith data element of L and return its value with e, and the length of L is reduced by 1
Status ListDelete(SqList *L, int i, ElemType *e) {
int k;
if (L->length == 0)
return ERROR;//The linear table is empty and cannot be deleted.
if (i < 1 || i > L->length)
return ERROR;//The deletion location is incorrect and cannot be deleted.
//Save the element to be deleted and return.
*e = L->data[i-1];
if (i<L->length){
for (k = i; k < L->length; k++) { // Start from left to right.
L->data[k-1] = L->data[k];//Move left one by one
}
}
L->length--;
return OK;
}
Time complexity:
The best case is O(1); The worst case is O(n).
Advantages and disadvantages of linear table and sequential table storage structure
Advantages:
-
No additional storage space is required to represent the relationship between the elements in the table.
-
You can quickly access elements anywhere in the table.
Disadvantages:
-
Insert and delete operations require moving a large number of elements.
-
When the length of linear table changes greatly, it is difficult to determine the capacity of storage space.
-
Causing "fragmentation" of storage space.
Code summary
#define MAXSIZE 20 / / initial allocation of storage space
typedef int ElemType; // The type of ElemType depends on the actual situation. Here, it is assumed to be int
typedef struct {
ElemType data[MAXSIZE]; // The array stores data elements, and the maximum value is MAXSIZE
int length; // Current length of linear table
} SqList;
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
// Status is the type of function, and its value is the status code of the result of the function, such as OK
// Initial recognition condition: sequential linear table l already exists, 1 ≤ i ≤ ListLength(L)
// Operation result: use e to return the value of the ith data element in L.
Status GetElem(SqList L, int i, ElemType *e) {
if (L.length == 0 || i < 1 || i > L.length)
return ERROR;
*e = L.data[i - 1];
return OK;
}
Status ListInsert(SqList *L, int i, ElemType e) {
int k;
if (L->length == MAXSIZE) //Linear table full
return ERROR;
if (i < 1 || i > L->length) //i do not meet the scope
return ERROR;
if (i <= L->length) { //Insert footer of data
for (k = L->length - 1; k >= i - 1; k--) {
L->data[k + 1] = L->data[k];//Move one bit to the right from the last one
}
}
L->data[i - 1] = e; //Insert new element
L->length++;
return OK;
}
//Delete element
//Initial condition: linear table l already exists, 1 ≤ i ≤ ListLength(L)
//Operation result: delete the ith data element of L and return its value with e, and the length of L is reduced by 1
Status ListDelete(SqList *L, int i, ElemType *e) {
int k;
if (L->length == 0)
return ERROR;//The linear table is empty and cannot be deleted.
if (i < 1 || i > L->length)
return ERROR;//The deletion location is incorrect and cannot be deleted.
//Save the element to be deleted and return.
*e = L->data[i - 1];
if (i < L->length) {
for (k = i; k < L->length; k++) { // Start from left to right.
L->data[k - 1] = L->data[k];//Move left one by one
}
}
L->length--;
return OK;
}
Chain storage structure of linear list
In order to represent the logical relationship between each data element ai and its direct successor data element ai+1, for data element ai, in addition to storing its own information, it is also necessary to store an information indicating its direct successor (i.e. the storage location of direct successor). We call the field storing data element information as data field, and the field storing direct successor positions as pointer field. The information stored in the pointer field is called a pointer or chain. These two parts of information constitute the storage image of data element ai, which is called node.
n nodes (storage image of ai) are linked into a linked list, which is the linked storage structure of linear list. Because each node of the linked list contains only one pointer field, it is called single linked list.
The storage location of the first node in the linked list is called the head pointer. The access of the whole linked list structure must start from the pointer. The pointer of the last node of the linked list is NULL. (NULL or represented by "^").
Sometimes, in order to facilitate the operation of the linked list, we will attach a node in front of the first node of the single linked list, which is called the head node. The data field of this header node can not store any information.
Similarities and differences between head pointer and head node
Head pointer
- Head pointer refers to the pointer of the linked list to the first node. If the linked list has a head node, it refers to the pointer to the head node.
- The head pointer has the function of identification, so the head pointer is often preceded by the name of the linked list.
- Whether the linked list is empty or not, the header pointer is not empty. The header pointer is a necessary element of the linked list.
Head node
- The head node is established for unified and convenient operation. If it is placed before the node of the first element, its data field is generally meaningless (it can also be used to store the length of the linked list).
- With the head node, the operation of inserting and deleting the first node before the first element node is unified with that of other nodes.
- The head node is not necessarily a necessary element of the linked list.
Code description of linear watch chain storage structure
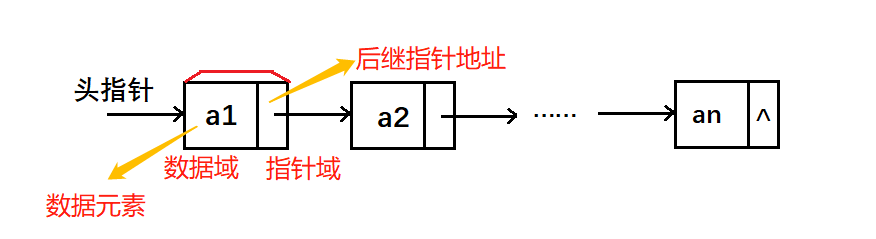
Single linked list of leading nodes

C language structure pointer describes single linked list nodes.
typedef int ElemType;
typedef struct Node {
ElemType data;
struct Node *next;
} Node;
typedef struct Node *LinkList; //Define LinkList
The node is composed of a data field for storing data elements and a pointer field for storing the addresses of subsequent nodes.
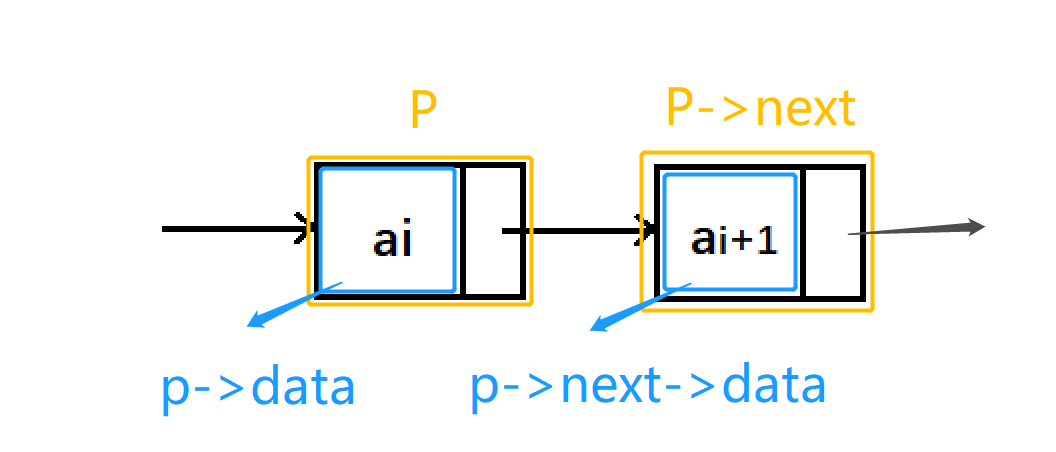
Reading of single linked list
Algorithm idea for obtaining the ith data in the linked list:
- Declare a pointer p to the first node of the linked list, and initialize j from 1;
- When J < I, traverse the linked list, make the pointer of P move backward and continuously point to the next node, and j accumulates 1;
- If p is empty at the end of the linked list, it indicates that the ith node does not exist;
- If the search is successful, p returns the data.
code implementation
//Initial condition: sequence table l already exists, 1 ≤ i ≤ ListLength(L);
//Operation result: use e to return the value of the ith data element.
Status GetElem(LinkList L, int i, ElemType *e) {
int j;
LinkList p; // Declare a pointer p
p = L->next; //p points to the first node of the linked list
j = 1;
while (p && j < i) {
p = p->next; //p points to the next pointer
j++;
}
if (!p || j > i)
return ERROR;
*e = p->data;
return OK;
}
To put it bluntly, it is to find it from the beginning until you know the ith node. Core idea: "work pointer moves back."
Time complexity analysis: best O(1), worst O(n). Looking for the first or the best, looking for the last or out of range, is the worst.
Insertion and deletion of single linked list
Suppose you want to insert node s between nodes p and p:
s->next = p->next;/
p->next = s;
The idea of inserting the ith data node in the single linked list:
The whole is to find the ith node first and then insert the node.
- Declare a pointer p to the head node of the linked list, and initialize j from 1;
- When J < I, traverse the linked list, make the pointer of p move backward and continuously point to the next node, and j accumulates 1;
- If p is empty at the end of the linked list, it indicates that the ith node does not exist;
- If the search is successful, an empty node s is generated in the system;
- Assign the data element e to s - > data;
- Standard statement for successful insertion of single linked list: S - > next = P - > next; p->next = s;
- Insert successfully and return.
Code implementation:
//Initial conditions: the sequential linear table l already exists; 1≤i≤ListLength(L)
//Operation result: insert a new data element e before the ith node in L, and add 1 to the length of L
Status ListInsert(LinkList *L,int i ,ElemType e){
int j;
LinkList p,s;
p = *L;
j = 1;
//Find the i-1 node
while (p&&j<i){
p = p->next;
j++;
}
if(!p||j>i)
return ERROR;
s = (LinkList)malloc(sizeof (Node));//Apply for a node space
s->data = e;
//Insert operation
s->next = p->next;
p->next = s;
return OK;
}
Deletion of single linked list
Delete a node in the linked list as long as:
p->next = p->next->next;
Algorithm idea of deleting the ith data node in the single linked list:
- Declare a pointer p to the head node of the linked list, and initialize j from 1;
- When J < I, traverse the linked list, make the pointer of p move backward and continuously point to the next node, and j accumulates 1;
- If the linked list reaches the end and p is empty, it indicates that the ith node does not exist
- Otherwise, if the search is successful, assign the value to be deleted to q;
- Deletion statement of single linked list: P - > next = P - > next - > next;
- Assign the data in the q node to e as the return value (instead of the return value, it is returned by accessing the address with a pointer).
- Release q node space
- Return success.
Code implementation:
//Initial conditions: the sequential linear table l already exists; 1≤i≤ListLength(L)
//Operation result: delete the ith node of L and return its value with e, and the length of L is reduced by 1
Status ListDelete(LinkList *L, int i, ElemType *e) {
int j;
LinkList p, q;
p = *L;
j = 1;
//Find the ith node
while (p->next && j < i) {
p = p->next;
j++;
}
if (!(p->next) || j > i)
return ERROR;
q = p->next;
p->next = q->next;//Equivalent to p - > next = P - > next - > next
*e = q->data;
free(q);
return OK;
}
For the whole algorithm. We can easily conclude that the time complexity of insertion and deletion is O(n), which is mainly due to the complexity of searching. Both insert and delete are O(1).
The whole table creation of single linked list
Algorithm idea for creating single linked table and whole table:
- Declare a pointer p and counter i;
- Initialize an empty linked list L;
- Let the pointer of the head node of L point to NULL, that is, establish a single linked list of the head node;
- Circular node creation:
- Generate a new node and assign it to p;
- Randomly generate a number assigned to the number field P - > data of p;
- Insert p between the head node and the previous new node.
// The whole table creation of single linked list
// Randomly generate the values of n elements and establish a single chain linear table with header nodes (header interpolation method)
void CreateListHead(LinkList *L,int n){
LinkList p;
int i;
srand(time(0)); //Initialize random seed
*L = (LinkList) malloc(sizeof (Node));
(*L)->next = NULL; //Establish a single linked list of leading nodes
for (i = 0; i < n; ++i) {
p = (LinkList) malloc(sizeof (Node));
p->data = rand()%100+1;
p->next = (*L)->next;
(*L)->next = p; //Insert the newly created node between the header and the next node of the original header
}
}
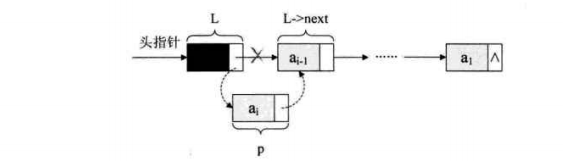
The above method is the head insertion method, which inserts the new node between the head node and the original head - > next. Another way is tail interpolation.
// Randomly generate the values of n elements and establish a single chain linear table with header nodes (tail interpolation method)
void CreateListTail(LinkList *L, int n) {
LinkList p, r; //p is used to represent the newly generated node, and r is used to represent the end of the queue node.
int i;
srand(time(0));
*L = (LinkList) malloc(sizeof(Node)); // Entire linear table
r = *L;
for (i = 0; i < n; ++i) {
p = (Node *) malloc(sizeof(Node)); //Generate a new node
p->data = rand() % 100 + 1;
//Now r is the end of the queue node that has generated the linked list, and p is the new node.
r->next = p; //Point the pointer of the terminal node at the end of the table to the new node
r = p; //Define the newly defined node as the end of the queue node
}
r->next = NULL; //Indicates the end of the current linked list
}
At the end of the loop, the pointer at the end of the queue should be set to null, so as to determine the end of the queue when traversing.
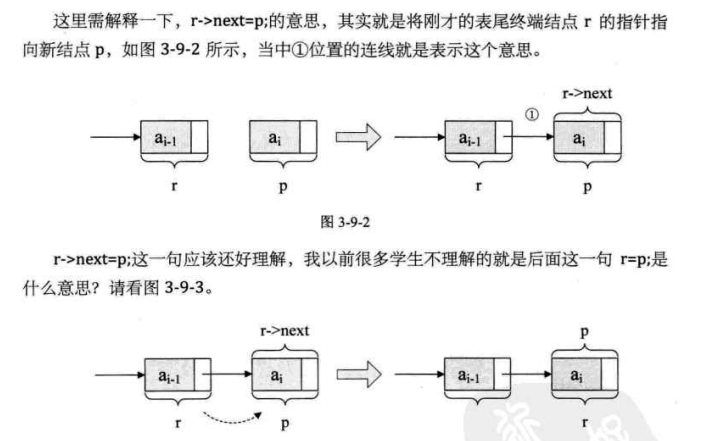
Delete the whole table of single linked list
Algorithm idea:
- Declare a node p and q;
- Assign the first node to p;
- loop
- Assign the next node to q;
- Release p
- Assign q to p.
Code implementation:
//Initial condition: sequence table L already exists.
//Action: reset L to empty table
Status ClearList(LinkList *L) {
LinkList p, q;
p = (*L)->next;
while (p) { //Not to the end of the team
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL;
return OK;
}
The current node can be released only after the backup of the current node to the next node is completed.
Advantages and disadvantages of single linked list structure and sequential storage structure
Storage method:
- The sequential storage structure uses a continuous storage unit to store the data elements of the linear table in turn.
- The single linked list adopts the chain storage structure, and a group of arbitrary storage units are used to store the elements of the linear list.
Time performance:
- lookup
- Sequential storage structure O(1)
- Single linked list O(n)
- Insert and delete
- The sequential storage structure needs to move half the elements of the average table length, and the time is O(n);
- After the pointer of a certain position appears in the single linked list, the insertion and deletion time is only O(1);
Spatial performance
- The sequential storage structure requires pre allocation of storage space, which is prone to overflow when it is large and small.
- Single linked list does not need to allocate storage space. It can be allocated as long as there is one, and the number of elements is not limited.
Through the above comparison, we draw some empirical conclusions:
- If the linear table needs to be searched frequently and there are few insert and delete operations, the sequential storage structure should be adopted. If frequent insertion and deletion are required, the single linked list structure should be adopted.
- When the number of elements in a linear table changes greatly, or you don't know how big it is, it's best to use a single linked list structure, so you don't need to consider the size of storage space.