Chapter 4 stack and queue
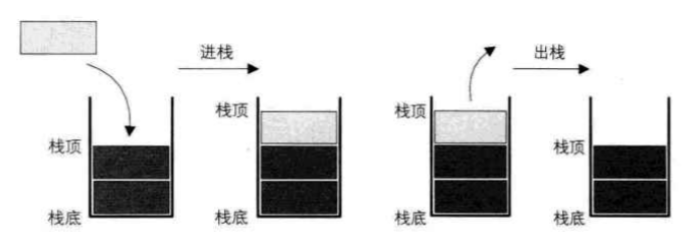
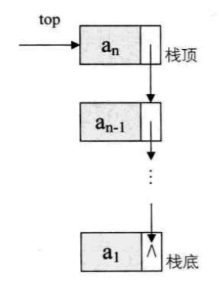
A stack is a linear table that is restricted to insert and delete operations only at the end of the table.
We call the end that allows insertion and deletion as the top of the stack, the other end as the bottom of the stack, and the stack without any data elements as an empty stack. Stack is also called last in first out linear table, or LIFO structure for short.
The insertion operation of stack is called entering stack, also known as pressing stack and entering stack. Like a bullet in a magazine. The deletion operation of stack is called out of stack, and some are also called bounce stack. Like a bullet in a magazine.
4.1 abstract data type of stack
For the stack, theoretically, it has the operation characteristics of linear table, but due to its particularity, there will be some changes in its operation. In particular, the insertion and deletion operations are renamed push and pop, which are easier to understand. You can think of it as a cartridge clip. Just press it in and pop it out. We usually call it in and out of the stack.
ADT Stack(stack)
Data
Same linear table. Elements have the same type, and adjacent elements have precursor and successor relationships
Operation
InitStack (*S):Initialize stack, create an empty operation S.
Destroystack (*s):If stack exists, destroy it. Clearstack(*s):Empty the stack.
stackEmpty(s):If the stack is empty, return true,Otherwise return false.
GetTop (s,*e):If the stack exists and is not empty, use e return S The top element of the stack.
Push(*s,e):If stack S Existing, insert new element e To stack S And become the top element of the stack.
Pop (*s,*e):Delete stack s Middle stack top element,Combined use e Returns its value.
StackLength(S):Return stack S Number of elements.
endADT
4.2 sequential storage structure and implementation of stack
4.2.1 sequential storage structure of stack
Since stack is a special case of linear table, the sequential storage of stack is actually a simplification of the sequential storage of linear table, which is called sequential stack for short. Linear tables are implemented by arrays. Think about it. For linear tables that can only be inserted and deleted at one end of the stack, which end of the array is better as the top and bottom of the stack?
Yes, yes, it's better to use the end with subscript 0 as the bottom of the stack, because the first element exists at the bottom of the stack and the change is the smallest, so let it be the bottom of the stack.
Let's look at the structure definition of the stack
typedef int SElemType; /* SElemType The type depends on the actual situation, which is assumed to be int */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* Pointer for stack top */
}SqStack;

4.2.2 stacking operation
/* Insert element e as the new stack top element */
Status Push(SqStack *S,SElemType e)
{
if(S->top == MAXSIZE -1) /* Stack full */
{
return ERROR;
}
S->top++; /* Stack top pointer increases by one */
S->data[S->top]=e; /* Assign the newly inserted element to the stack top space */
return OK;
}

4.2.2 stack out operation
/* If the stack is not empty, delete the top element of S, return its value with e, and return OK; Otherwise, ERROR is returned */
Status Pop(SqStack *S,SElemType *e)
{
if(S->top==-1)
return ERROR;
*e=S->data[S->top]; /* Assign the stack top element to be deleted to e */
S->top--; /* Stack top pointer minus one */
return OK;
}
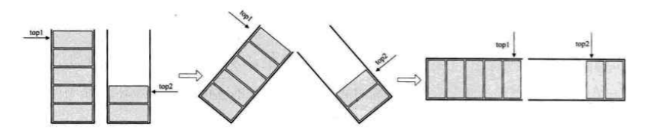
4.3 shared space of two stacks
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;
typedef int SElemType; /* SElemType The type depends on the actual situation, which is assumed to be int */
/* Two stack shared space structure */
typedef struct
{
SElemType data[MAXSIZE];
int top1; /* Stack 1 stack top pointer */
int top2; /* Stack 2 stack top pointer */
}SqDoubleStack;
Status visit(SElemType c)
{
printf("%d ",c);
return OK;
}
/* Construct an empty stack S */
Status InitStack(SqDoubleStack *S)
{
S->top1=-1;
S->top2=MAXSIZE;
return OK;
}
/* Set S to empty stack */
Status ClearStack(SqDoubleStack *S)
{
S->top1=-1;
S->top2=MAXSIZE;
return OK;
}
/* If stack S is an empty stack, it returns TRUE; otherwise, it returns FALSE */
Status StackEmpty(SqDoubleStack S)
{
if (S.top1==-1 && S.top2==MAXSIZE)
return TRUE;
else
return FALSE;
}
/* Returns the number of elements of S, that is, the length of the stack */
int StackLength(SqDoubleStack S)
{
return (S.top1+1)+(MAXSIZE-S.top2);
}
/* The new element at the top of the stack is e */
Status Push(SqDoubleStack *S,SElemType e,int stackNumber)
{
if (S->top1+1==S->top2) /* The stack is full and cannot push new elements */
return ERROR;
if (stackNumber==1) /* There are elements in stack 1 */
S->data[++S->top1]=e; /* If it is stack 1, first top1+1 and then assign a value to the array element. */
else if (stackNumber==2) /* There are elements in stack 2 */
S->data[--S->top2]=e; /* If it is stack 2, first top2-1 and then assign a value to the array element. */
return OK;
}
/* If the stack is not empty, delete the top element of S, return its value with e, and return OK; Otherwise, ERROR is returned */
Status Pop(SqDoubleStack *S,SElemType *e,int stackNumber)
{
if (stackNumber==1)
{
if (S->top1==-1)
return ERROR; /* Description stack 1 is empty and overflows */
*e=S->data[S->top1--]; /* Take the top element of stack 1 out of the stack */
}
else if (stackNumber==2)
{
if (S->top2==MAXSIZE)
return ERROR; /* Description stack 2 is empty and overflows */
*e=S->data[S->top2++]; /* Take the top element of stack 2 out of the stack */
}
return OK;
}
Status StackTraverse(SqDoubleStack S)
{
int i;
i=0;
while(i<=S.top1)
{
visit(S.data[i++]);
}
i=S.top2;
while(i<MAXSIZE)
{
visit(S.data[i++]);
}
printf("\n");
return OK;
}
int main()
{
int j;
SqDoubleStack s;
int e;
if(InitStack(&s)==OK)
{
for(j=1;j<=5;j++)
Push(&s,j,1);
for(j=MAXSIZE;j>=MAXSIZE-2;j--)
Push(&s,j,2);
}
printf("The elements in the stack are:");
StackTraverse(s);
printf("The elements in the current stack are:%d \n",StackLength(s));
Pop(&s,&e,2);
printf("Pop up stack top element e=%d\n",e);
printf("Stack empty No:%d(1:Null 0:no)\n",StackEmpty(s));
for(j=6;j<=MAXSIZE-2;j++)
Push(&s,j,1);
printf("The elements in the stack are:");
StackTraverse(s);
printf("Stack full:%d(1:No 0:full)\n",Push(&s,100,1));
ClearStack(&s);
printf("Empty stack after emptying stack No:%d(1:Null 0:no)\n",StackEmpty(s));
return 0;
}
4.4 chain storage and implementation of stack
Stack chain for short.
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;
typedef int SElemType; /* SElemType The type depends on the actual situation, which is assumed to be int */
/* Chain stack structure */
typedef struct StackNode
{
SElemType data;
struct StackNode *next;
}StackNode,*LinkStackPtr;
typedef struct
{
LinkStackPtr top;
int count;
}LinkStack;
Status visit(SElemType c)
{
printf("%d ",c);
return OK;
}
/* Construct an empty stack S */
Status InitStack(LinkStack *S)
{
S->top = (LinkStackPtr)malloc(sizeof(StackNode));
if(!S->top)
return ERROR;
S->top=NULL;
S->count=0;
return OK;
}
/* Set S to empty stack */
Status ClearStack(LinkStack *S)
{
LinkStackPtr p,q;
p=S->top;
while(p)
{
q=p;
p=p->next;
free(q);
}
S->count=0;
return OK;
}
/* If stack S is an empty stack, it returns TRUE; otherwise, it returns FALSE */
Status StackEmpty(LinkStack S)
{
if (S.count==0)
return TRUE;
else
return FALSE;
}
/* Returns the number of elements of S, that is, the length of the stack */
int StackLength(LinkStack S)
{
return S.count;
}
/* If the stack is not empty, use e to return the top element of S and return OK; Otherwise, ERROR is returned */
Status GetTop(LinkStack S,SElemType *e)
{
if (S.top==NULL)
return ERROR;
else
*e=S.top->data;
return OK;
}
/* Insert element e as the new stack top element */
Status Push(LinkStack *S,SElemType e)
{
LinkStackPtr s=(LinkStackPtr)malloc(sizeof(StackNode));
s->data=e;
s->next=S->top; /* Assign the current stack top element to the direct successor of the new node, as shown in figure ① */
S->top=s; /* Assign the new node s to the stack top pointer, as shown in figure ② */
S->count++;
return OK;
}
/* If the stack is not empty, delete the top element of S, return its value with e, and return OK; Otherwise, ERROR is returned */
Status Pop(LinkStack *S,SElemType *e)
{
LinkStackPtr p;
if(StackEmpty(*S))
return ERROR;
*e=S->top->data;
p=S->top; /* Assign the top node of the stack to p, as shown in figure ③ */
S->top=S->top->next; /* Make the pointer at the top of the stack move down one bit and point to the next node, as shown in figure ④ */
free(p); /* Release node p */
S->count--;
return OK;
}
Status StackTraverse(LinkStack S)
{
LinkStackPtr p;
p=S.top;
while(p)
{
visit(p->data);
p=p->next;
}
printf("\n");
return OK;
}
int main()
{
int j;
LinkStack s;
int e;
if(InitStack(&s)==OK)
for(j=1;j<=10;j++)
Push(&s,j);
printf("The elements in the stack are:");
StackTraverse(s);
Pop(&s,&e);
printf("Pop up stack top element e=%d\n",e);
printf("Stack empty No:%d(1:Null 0:no)\n",StackEmpty(s));
GetTop(s,&e);
printf("Stack top element e=%d Stack length is%d\n",e,StackLength(s));
ClearStack(&s);
printf("Empty stack after emptying stack No:%d(1:Null 0:no)\n",StackEmpty(s));
return 0;
}
4.5 application of stack
Binary conversion
#include <iostream>
#define ElemType int
#define INIT_SIZE 10 / / initial capacity
#define INCRE_SIZE 20 / / self increment
//Defines a stack of sequential storage
typedef struct
{
ElemType *base; //Stack bottom pointer
ElemType *top; //Stack top pointer
int stackSize; //Maximum capacity
} sqStack;
//initialization
void initStack(sqStack *s)
{
s->base = (ElemType *)malloc(INIT_SIZE * sizeof(ElemType));
if (!s->base)
{
exit(0);
}
s->top = s->base; //Initialization, the top of the stack is the bottom of the stack
s->stackSize = INIT_SIZE;
}
void push(sqStack *s, ElemType e)
{
if (s->top - s->base == s->stackSize)
{ //Judge whether the stack is full and add space
//realloc copies the original memory into a new piece of memory
s->base = (ElemType *)realloc(s->base, (s->stackSize + INCRE_SIZE) * sizeof(ElemType));
if (!s->base)
{
exit(0);
}
s->top = s->base + s->stackSize; //Set new stack top
s->stackSize = s->stackSize + INCRE_SIZE; //Reset maximum
}
*(s->top)++ = e;
}
ElemType pop(sqStack *s)
{
if (s->top == s->base)
{
std::cout << "Stack is empty" << std::endl;
return -1;
}
return *(--s->top);
}
//Empty the stack and let the top of the stack return to the bottom of the stack
void clearStack(sqStack *s)
{
s->top = s->base;
}
//Destroy stack (different from emptying)
void destroyStack(sqStack *s)
{
s->top = s->base;
//Free up the memory space allocated for this stack,
//In malloc, the system will remember the starting address and size of the applied continuous space,
//Free, as long as the starting address is told to the system, the system will know how much space will be free
free(s->base);
s->stackSize = 0;
}
ElemType size(sqStack *s){
return s->top-s->base;
}
int main()
{
sqStack s;
initStack(&s);
std::cout << "Please enter binary number,#End of sign "< < STD:: endl;
char c;
scanf("%c",&c);
while(c!='#'){
push(&s,c-48); //The ascii code of 0 is 48, so 1-0 = 1
scanf("%c",&c);
}
getchar();
int n =1,sum=0;
while(s.base!=s.top){
sum += pop(&s) * n;
n *= 2;
}
std::cout << "Decimal number is:" << sum << std::endl;
return 0;
}
Evaluation of four arithmetic expressions
In the 1950s, Polish logician Jan Eukasiewicz came up with a suffix expression without brackets, which we also call Reverse Polish Notation (RPN). I think maybe his name is too complicated, so future generations only use his nationality instead of his name. This suffix representation is a new display method of expression, which skillfully solves the problem of four operations in the program.
For "9 + (3-1) × 3 + 10 ÷ 2 ", if you want to use the suffix representation, what should it look like:" 9 3 1 - 3 * + 10 2 / + ", such an expression is called the suffix expression. The reason why it is called the suffix is that all symbols appear after the number to be calculated. Obviously, there are no parentheses here. For students who have never been in contact with suffix expressions, such expressions are very uncomfortable.
int main()
{
sqStack s;
initStack(&s);
std::cout << "Please press the inverse Polish expression to enter data,Numbers are separated by spaces,#End of sign "< < STD:: endl;
char c;
ElemType p,q;
scanf("%c",&c);
while(c!='#'){
if(c != ' '){
switch(c){
case '+':
p = pop(&s);
q = pop(&s);
push(&s,q+p);
break;
case '-':
p = pop(&s);
q = pop(&s);
push(&s,q-p);
break;
case '*':
p = pop(&s);
q = pop(&s);
push(&s,q*p);
break;
case '/':
p = pop(&s);
q = pop(&s);
push(&s,q/p);
break;
default:
push(&s,c-48);
}
}
scanf("%c",&c);
}
getchar();
std::cout << "The suffix expression evaluates to:" << pop(&s) << std::endl;
return 0;
}
//Rewriting program: you can calculate decimals
typedef double ElemType;
int main()
{
sqStack s;
initStack(&s);
std::cout << "Please press the inverse Polish expression to enter data,Numbers are separated by spaces,#End of sign "< < STD:: endl;
char c;
char str[5];//Assume a maximum of 4 characters
int i=0;
ElemType p, q, d;
scanf("%c", &c);
while (c != '#')
{
while (isdigit(c) || c == '.')
{ //Filter numbers or decimals
str[i++] = c;
str[i] = '\0'; //The end is 0, and the number will be overwritten next time
if(i>=5){
printf("The input number is too large");
exit(0);
}
scanf("%c", &c);
if (c == ' ')
{
push(&s, atof(str));
i = 0;
break;
}
}
if (c != ' ')
{
switch (c)
{
case '+':
p = pop(&s);
q = pop(&s);
push(&s, q + p);
break;
case '-':
p = pop(&s);
q = pop(&s);
push(&s, q - p);
break;
case '*':
p = pop(&s);
q = pop(&s);
push(&s, q * p);
break;
case '/':
p = pop(&s);
q = pop(&s);
push(&s, q / p);
break;
}
}
scanf("%c", &c);
}
getchar();
std::cout << "The calculation result is:" << pop(&s) << std::endl;
return 0;
}
We put the standard four arithmetic expressions used at ordinary times, namely "9 + (3-1) × 3 + 10 ÷ 2 "is called infix expression. Because all operation symbols are in the middle of two numbers, now our problem is the conversion from infix to suffix. 9+(3-1)*3+10/2 —> 9 3 1 - 3 * + 10 2 / +
Summary rule: traverse each number and symbol of infix expression from left to right. If it is a number, it will be output directly. If it is a symbol, it will judge its priority with the symbol at the top of the stack. If it is a right bracket or the priority is lower than the symbol at the top of the stack, the elements at the top of the stack will be out of the stack and output in turn. The last symbol will not be put into the stack until it meets the left bracket or empty stack.
typedef char ElemType; //Stack symbol
int main()
{
sqStack s;
initStack(&s);
std::cout << "Please enter infix expression,#End of sign "< < STD:: endl;
char c;
int i = 0;
ElemType p, q, d;
scanf("%c", &c);
while (c != '#')
{
while (c >= '0' && c <= '9')
{
printf("%c", c);
scanf("%c", &c);
if (!isdigit(c))
{
printf(" ");
}
}
if (c == '#')
{
break;
}
if (c == ')')
{
ElemType e = pop(&s);
printf("%c ", e);
pop(&s);
}
if (c == '+' || c == '-')
{
if (s.top == s.base)
{ //If the stack is empty, push directly because the + - priority is the lowest
push(&s, c);
}
else
{
ElemType e;
do
{
e = pop(&s);
if (e == '(') //If the left bracket is at the top of the stack, continue to push
{
push(&s, c);
}
else //If it is other symbols, it will be output until the stack is empty or the left bracket is encountered again
{
printf("%c ", e);
}
} while (s.top != s.base && e != '(');
push(&s, c);
}
}
if (c == '*' || c == '/' || c == '(')
{
push(&s, c);
}
scanf("%c", &c);
}
getchar();
while (s.base != s.top)//Finally, there is the expression, full pop
{
c = pop(&s);
printf("%c ", c);
}
return 0;
}
4.6 definition of queue
A queue is a linear table that only allows insertion at one end and deletion at the other.
Queue is a first in first out linear table, called FIFO for short. The end that allows insertion is called the tail of the queue, and the end that allows deletion is called the head of the queue. Suppose the queue is q = (a1, a2,..., an), then a1 is the head element and an is the tail element. In this way, we can always start from a1 when deleting, and last when inserting.

4.7 abstract data type of queue
ADT queue(queue)
Data
Same linear table. Elements have the same type, and adjacent elements have precursor and successor relationships
Operation
InitQueue (*o):Initialization operation,Create an empty queue Q.
DestroyQueue (*o):If queue Q If it exists, destroy it.
ClearQueue (*o):Queue Q Empty.
QueueEmpty (o):If queue Q Null, return true,Otherwise return false.
GetHead(o,*e):If queue Q Exist and not empty, use e Return queue Q Team leader element.
EnQueue (*o,e):If queue Q Existing, insert new element e To queue Q And become the tail element.
DeQueue (*o, *e):Delete queue Q Squadron head element, and use e Returns its value.
QueueLength(o):Return queue Q Number of elements
endADT
4.8 circular queue
In order to avoid that when there is only one element, the head of the queue and the tail of the queue coincide, which makes the processing troublesome, two pointers are introduced. The front pointer points to the head of the queue element and the rear pointer points to the next position of the tail of the queue element. In this way, when front is equal to rear, the queue is not an element left, but an empty queue. We call this sequential storage structure of queue head to tail as circular queue.
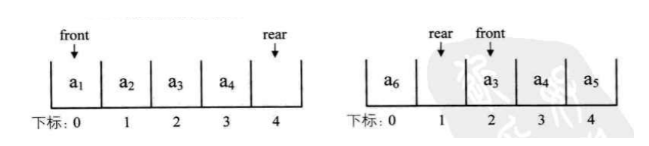
The condition that the queue is full is (rear + 1)% queuesize = = front (the purpose of taking the module "%" is to integrate the size of rear and front into one problem).
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;
typedef int QElemType; /* QElemType The type depends on the actual situation, which is assumed to be int */
/* Sequential storage structure of circular queue */
typedef struct
{
QElemType data[MAXSIZE];
int front; /* Head pointer */
int rear; /* Tail pointer. If the queue is not empty, it points to the next position of the tail element of the queue */
}SqQueue;
Status visit(QElemType c)
{
printf("%d ",c);
return OK;
}
/* Initialize an empty queue Q */
Status InitQueue(SqQueue *Q)
{
Q->front=0;
Q->rear=0;
return OK;
}
/* Clear Q to empty queue */
Status ClearQueue(SqQueue *Q)
{
Q->front=Q->rear=0;
return OK;
}
/* If queue Q is an empty queue, it returns TRUE; otherwise, it returns FALSE */
Status QueueEmpty(SqQueue Q)
{
if(Q.front==Q.rear) /* Flag of empty queue */
return TRUE;
else
return FALSE;
}
/* Returns the number of elements of Q, that is, the current length of the queue */
int QueueLength(SqQueue Q)
{
return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
}
/* If the queue is not empty, use e to return the queue header element of Q and return OK; otherwise, return ERROR */
Status GetHead(SqQueue Q,QElemType *e)
{
if(Q.front==Q.rear) /* queue is empty */
return ERROR;
*e=Q.data[Q.front];
return OK;
}
/* If the queue is not full, insert a new tail element with element e as Q */
Status EnQueue(SqQueue *Q,QElemType e)
{
if ((Q->rear+1)%MAXSIZE == Q->front) /* Queue full judgment */
return ERROR;
Q->data[Q->rear]=e; /* Assign the element e to the end of the queue */
Q->rear=(Q->rear+1)%MAXSIZE;/* rear Move the pointer back one position, */
/* If to the end, go to the array header */
return OK;
}
/* If the queue is not empty, delete the Q squadron header element and return its value with e */
Status DeQueue(SqQueue *Q,QElemType *e)
{
if (Q->front == Q->rear) /* Judgment of empty queue */
return ERROR;
*e=Q->data[Q->front]; /* Assign the team head element to e */
Q->front=(Q->front+1)%MAXSIZE; /* front Move the pointer back one position, */
/* If to the end, go to the array header */
return OK;
}
/* Each element in queue Q is output from the head of the queue to the tail of the queue */
Status QueueTraverse(SqQueue Q)
{
int i;
i=Q.front;
while((i+Q.front)!=Q.rear)
{
visit(Q.data[i]);
i=(i+1)%MAXSIZE;
}
printf("\n");
return OK;
}
int main()
{
Status j;
int i=0,l;
QElemType d;
SqQueue Q;
InitQueue(&Q);
printf("After initializing the queue, is the queue empty?%u(1:Null 0:no)\n",QueueEmpty(Q));
printf("Please enter an integer queue element(No more than%d individual),-1 Is an early Terminator: ",MAXSIZE-1);
do
{
/* scanf("%d",&d); */
d=i+100;
if(d==-1)
break;
i++;
EnQueue(&Q,d);
}while(i<MAXSIZE-1);
printf("Queue length is: %d\n",QueueLength(Q));
printf("Is the queue empty now?%u(1:Null 0:no)\n",QueueEmpty(Q));
printf("continuity%d Delete element by team leader,Insert element at end of queue:\n",MAXSIZE);
for(l=1;l<=MAXSIZE;l++)
{
DeQueue(&Q,&d);
printf("The deleted element is%d,Inserted element:%d \n",d,l+1000);
/* scanf("%d",&d); */
d=l+1000;
EnQueue(&Q,d);
}
l=QueueLength(Q);
printf("Now the elements in the queue are: \n");
QueueTraverse(Q);
printf("We've inserted it at the end of the team%d Elements\n",i+MAXSIZE);
if(l-2>0)
printf("Now deleted by team leader%d Elements:\n",l-2);
while(QueueLength(Q)>2)
{
DeQueue(&Q,&d);
printf("The deleted element value is%d\n",d);
}
j=GetHead(Q,&d);
if(j)
printf("Now the team head element is: %d\n",d);
ClearQueue(&Q);
printf("After emptying the queue, Is the queue empty?%u(1:Null 0:no)\n",QueueEmpty(Q));
return 0;
}
From this explanation, you should find that the time performance of the algorithm is not high if it is only sequential storage, but the circular queue is faced with the problem that the array may overflow. Therefore, we also need to study the chain storage structure that does not need to worry about the queue length.
4.9 chain storage structure and implementation of queue
The chain storage structure of queue is actually a single chain list of linear table, but it can only end in and end out. We call it chain queue for short. For the convenience of operation, we point the queue head pointer to the head node of the chain queue, and the queue tail pointer to the terminal node. When the queue is empty, both front and rear point to the head node.

#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;
typedef int QElemType; /* QElemType The type depends on the actual situation, which is assumed to be int */
typedef struct QNode /* Node structure */
{
QElemType data;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct /* Linked list structure of queue */
{
QueuePtr front,rear; /* Head and tail pointer */
}LinkQueue;
Status visit(QElemType c)
{
printf("%d ",c);
return OK;
}
/* Construct an empty queue Q */
Status InitQueue(LinkQueue *Q)
{
Q->front=Q->rear=(QueuePtr)malloc(sizeof(QNode));
if(!Q->front)
exit(OVERFLOW);
Q->front->next=NULL;
return OK;
}
/* Destroy queue Q */
Status DestroyQueue(LinkQueue *Q)
{
while(Q->front)
{
Q->rear=Q->front->next;
free(Q->front);
Q->front=Q->rear;
}
return OK;
}
/* Clear Q to empty queue */
Status ClearQueue(LinkQueue *Q)
{
QueuePtr p,q;
Q->rear=Q->front;
p=Q->front->next;
Q->front->next=NULL;
while(p)
{
q=p;
p=p->next;
free(q);
}
return OK;
}
/* If Q is an empty queue, it returns TRUE; otherwise, it returns FALSE */
Status QueueEmpty(LinkQueue Q)
{
if(Q.front==Q.rear)
return TRUE;
else
return FALSE;
}
/* Find the length of the queue */
int QueueLength(LinkQueue Q)
{
int i=0;
QueuePtr p;
p=Q.front;
while(Q.rear!=p)
{
i++;
p=p->next;
}
return i;
}
/* If the queue is not empty, use e to return the queue header element of Q and return OK; otherwise, return ERROR */
Status GetHead(LinkQueue Q,QElemType *e)
{
QueuePtr p;
if(Q.front==Q.rear)
return ERROR;
p=Q.front->next;
*e=p->data;
return OK;
}
/* Insert a new tail element with element e as Q */
Status EnQueue(LinkQueue *Q,QElemType e)
{
QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
if(!s) /* Storage allocation failed */
exit(OVERFLOW);
s->data=e;
s->next=NULL;
Q->rear->next=s; /* Assign the new node s with element e to the successor of the original team tail node, as shown in figure ① */
Q->rear=s; /* Set the current s as the end of the queue node, and the rear points to s, as shown in figure ② */
return OK;
}
/* If the queue is not empty, delete the queue header element of Q, return its value with e, and return OK; otherwise, return ERROR */
Status DeQueue(LinkQueue *Q,QElemType *e)
{
QueuePtr p;
if(Q->front==Q->rear)
return ERROR;
p=Q->front->next; /* Temporarily save the queue head node to be deleted to p, as shown in figure ① */
*e=p->data; /* Assign the value of the queue head node to be deleted to e */
Q->front->next=p->next;/* Assign the successor p - > next of the original team's head node to the successor of the head node, as shown in figure ② */
if(Q->rear==p) /* If the head of the queue is the tail of the queue, point the rear to the head node after deletion, as shown in figure ③ */
Q->rear=Q->front;
free(p);
return OK;
}
/* Each element in queue Q is output from the head of the queue to the tail of the queue */
Status QueueTraverse(LinkQueue Q)
{
QueuePtr p;
p=Q.front->next;
while(p)
{
visit(p->data);
p=p->next;
}
printf("\n");
return OK;
}
int main()
{
int i;
QElemType d;
LinkQueue q;
i=InitQueue(&q);
if(i)
printf("Successfully constructed an empty queue!\n");
printf("Empty queue?%d(1:Null 0:no) ",QueueEmpty(q));
printf("The length of the queue is%d\n",QueueLength(q));
EnQueue(&q,-5);
EnQueue(&q,5);
EnQueue(&q,10);
printf("Insert 3 elements(-5,5,10)after,The length of the queue is%d\n",QueueLength(q));
printf("Empty queue?%d(1:Null 0:no) ",QueueEmpty(q));
printf("The elements of the queue are:");
QueueTraverse(q);
i=GetHead(q,&d);
if(i==OK)
printf("The team head elements are:%d\n",d);
DeQueue(&q,&d);
printf("The team head element was deleted%d\n",d);
i=GetHead(q,&d);
if(i==OK)
printf("The new team leader elements are:%d\n",d);
ClearQueue(&q);
printf("After emptying the queue,q.front=%u q.rear=%u q.front->next=%u\n",q.front,q.rear,q.front->next);
DestroyQueue(&q);
printf("After destroying the queue,q.front=%u q.rear=%u\n",q.front, q.rear);
return 0;
}
4.10 summary and review
This chapter is about stacks and queues. They are special linear tables, but they limit the insertion and deletion operations.
A stack is a linear table that is restricted to insert and delete operations only at the end of the table.
A queue is a linear table that only allows insertion at one end and deletion at the other.
They can all be realized by the sequential storage structure of linear table, but they all have some disadvantages of sequential storage. Therefore, they have their own solving skills. For the stack, if it is two stacks with the same data type, the method of using both ends of the array as the bottom of the stack can be used to make the two stacks share data, which can maximize the space of the array. For queues, in order to avoid moving data during array insertion and deletion, circular queues are introduced, so that the head and tail of the queue can change circularly in the array. The time loss of mobile data is solved, so that the time complexity of inserting and deleting is O(n) becomes 0 (1).
They can also be realized through the chain storage structure, which is basically the same as the linear table in principle
- Stack
- Sequential stack
- Two stack shared space
- Stack chain
- Sequential stack
- queue
- Sequential queue
- Circular queue
- Chain queue
- Sequential queue