Graph traversal: starting from a vertex of a connected graph, access and traverse all vertices in the graph along some edges, and each vertex is accessed only once. This is called graph traversal, which is the basic operation of the graph

Traversal essence: the process of finding the adjacency point of each vertex

Characteristics of graph: there may be loops in the graph, and any vertex of the graph may be connected with other vertices. After accessing a vertex, it may return to the visited vertex along some edges

Solution: set the auxiliary array visited[n] to record the accessed vertices. 0 is not accessed and 1 is accessed

Figure common traversal methods:

• Depth_First Search (DFS)

• Breadth_First Search (BFS)

###Depth first search###

 

 

 

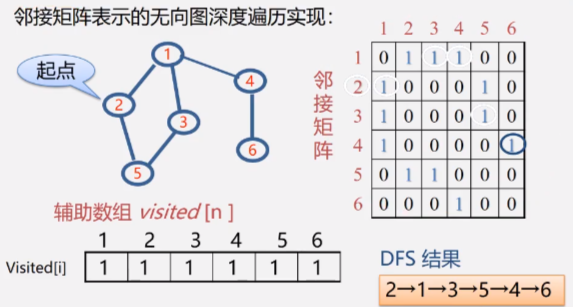
//Implementation of depth first search traversal of undirected graph represented by adjacency matrix
void DFS(AMGraph G, int v) {//Figure G shows the type of adjacency matrix
    //visited is a static array of type static
    cout<<v; visited[v]=true;//Access vertex v, start vertex
    for (int w=0; w<G.vexnum; w++)//Check the row of adjacency matrix v in turn
        if (G.arcs[v][w]&&!visited[w]) DFS(G, w);//Depth search starting from the current vertex
        //w is the adjacency point of v. if w is not accessed, DFS is called recursively
    //The for end of a DFS indicates that its adjacency points have been accessed
}//Code scanning is required for each row and column, and the time complexity is O(n square)
​
//Implementation of depth first search traversal of undirected graph represented by adjacency table
void DFS(ALGraph G, int v) {
    //visited is a static variable
    cout<<G.vertices[v].data; visited[v]=true;
    ArcNode* p=G.firstarc;
    while (p)
        if (!visited[p->adjvex]) {DFS(G, p->adjvex); p->nextarc;}
}//Time complexity o(n+e)
​
//A non connected graph is a sequential depth first search to access each connected graph

###Breadth first search###

Similar to virus propagation, access all its adjacent points with the vertex as the center of the circle, and access the adjacent points of the adjacent points

Unconnected graphs are connected graphs that are accessed by breadth first search in turn

The visited array is also required. This traversal method is very similar to the hierarchical traversal of the tree, so it can also be implemented with queues

void BFS(Graph G, int v) {//Non recursive traversal of connected graph G by breadth first
    cout<<v; visit[v]=true;//Access the v-th vertex
    InitQueue(Q);//Auxiliary queue initialization, null
    EnQueue(Q, v);//v join the team
    while (!QueueEmpty(Q)) {//Queue is not empty
        DeQueue(Q, u);//The header element is out of the queue and set to u
        for (w=FirstAdjVex(G, u); w>=0; w=NextAdjVex(G, u, w))
            //If W is an adjacent vertex of u that has not been accessed, w > = 0 indicates that there is an adjacent vertex, and if not, it is - 1. Exit the loop
            if (!visited[w]) {cout<<w; visit[w]=true; EnQueue(Q, w);}//w join the team
    }
}

###Comparison of efficiency between depth first search and breadth first search###

• The space complexity is the same, which is O(n) (borrowed stack or queue)

• The time complexity is only related to the storage structure (adjacency matrix or adjacency table), and has nothing to do with the search path

###Application of graph###

Application 1: minimum spanning tree

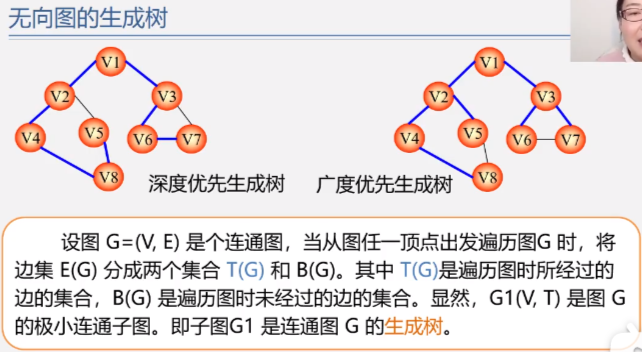
Spanning tree: contains all vertices of a connected graph, but removes some edges, but remains connected without loops (rings)

A graph can have many different spanning trees

All spanning trees have the following common characteristics:

• The number of vertices of the spanning tree is the same as that of the graph

• Spanning tree is the smallest connected subgraph of a graph, and it is unconnected without one edge

• The spanning tree of a connected graph with n vertices has n-1 edges

• Adding another edge to the spanning tree will inevitably form a loop

• The path between any two vertices in the spanning tree is unique

• A graph can have many different spanning trees

• A graph with n vertices and n-1 edges is not necessarily a spanning tree

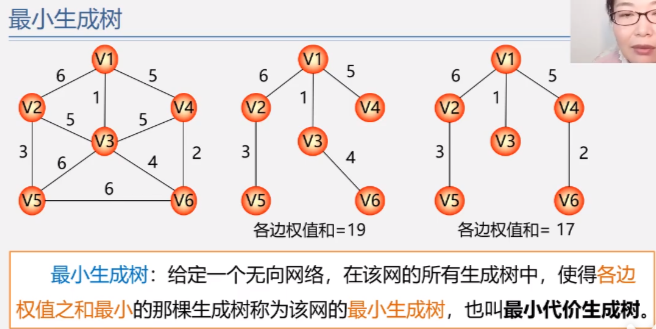
Typical applications of minimum spanning tree:

• To establish a communication network among n cities, n-1 roads should be paved in n cities

• However, because each line has economic cost, and there are at most n(n-1)/2 lines in n cities, how to select n-1 lines to minimize the total cost?

Abstract the mathematical model: obviously, this is a minimum spanning tree

• Apex - City, n

• Side - line, n-1

• Weight of edge - represents the economic cost of the line

• China Unicom Network -- the communication network of n cities

Construct Minimum Spanning Tree (MST)

Method 1 for constructing minimum spanning tree: Prim algorithm

 

Method 2 of constructing minimum spanning tree: Kruskal algorithm

 

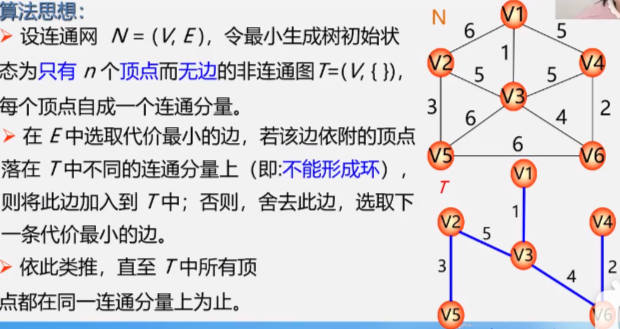
Comparison between Prim algorithm and Kruskal algorithm

 

Application 2: shortest path

Traffic problem solving: is there a highway connecting from place a to place B? When there are multiple paths, which is the shortest?

The traffic network is represented by a directed graph:

• Vertex - indicates the location

• Arc - indicates that two places are connected

• Weight on the arc - represents the distance between the two places, transportation cost or time spent in the diagram, etc

The first kind of question: how can the transportation time from one place to another be the shortest or the freight cost be the least? This is a problem of finding the minimum path between two points

Problem abstraction: find a path with the smallest sum of the weights of each edge among the multiple paths from the source point to the end point in the directed network

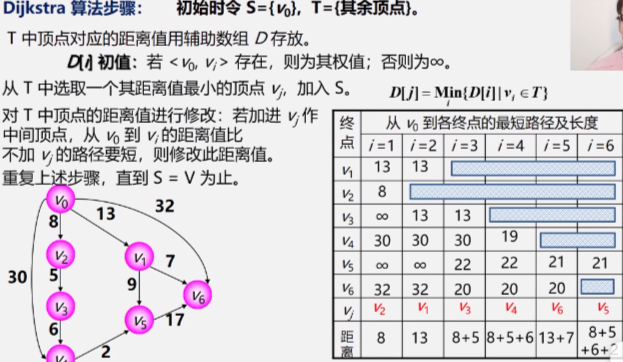
The second kind of problem: the shortest path from a source point to other vertices

 

Dijkstra algorithm} time complexity O(n2)

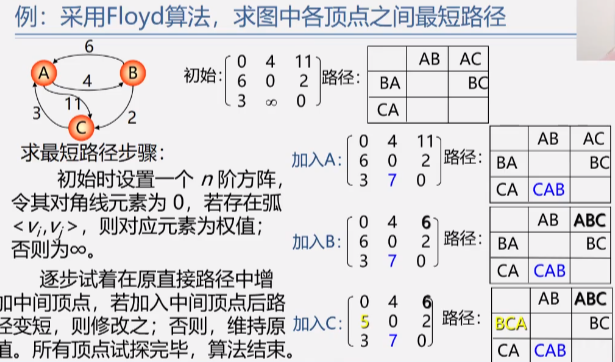
Floyd algorithm

 

Application 3: topology sorting

Directed acyclic graph (DAG)

 

 

 

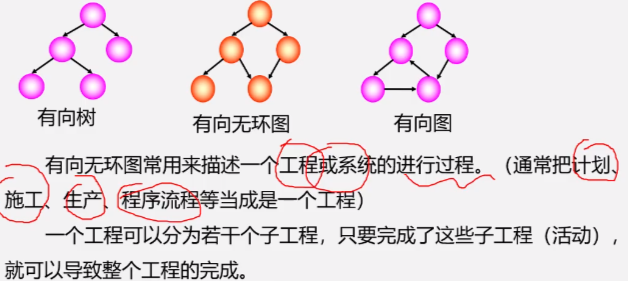
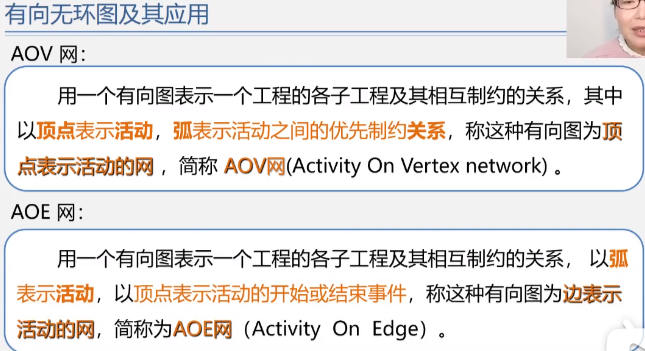
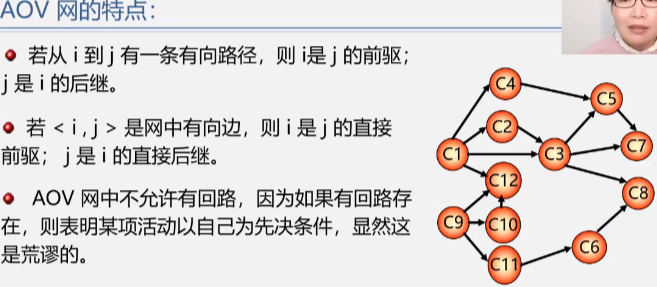
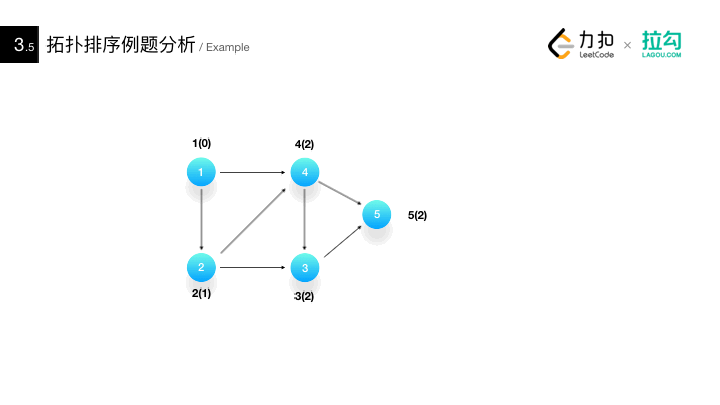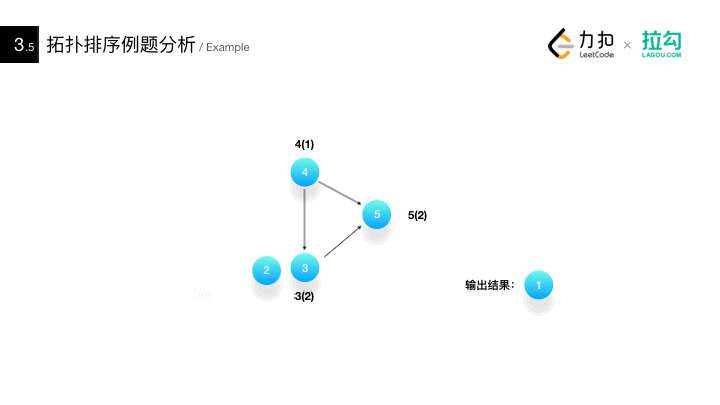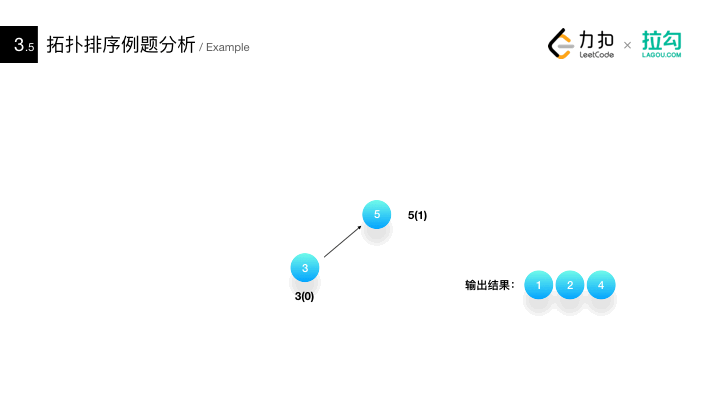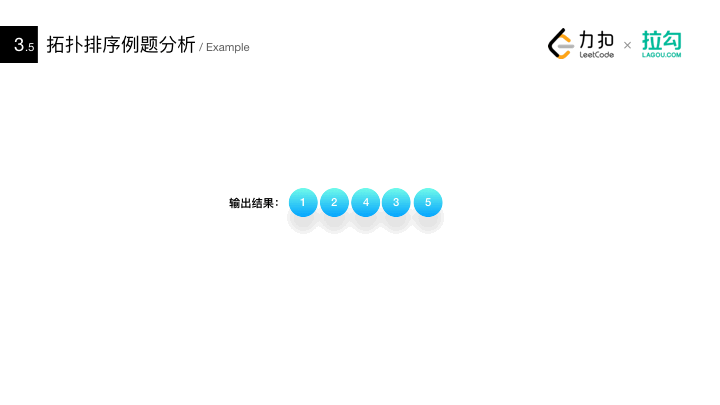
Method for detecting whether there are rings in AOV network: * construct the topological ordered sequence of its vertices for a directed graph. If all vertices in the network are in its topological ordered sequence, there must be no rings in the AOV network. On the contrary, there must be a loop*

Application 4: critical path

 

 

 

 ​​​​​

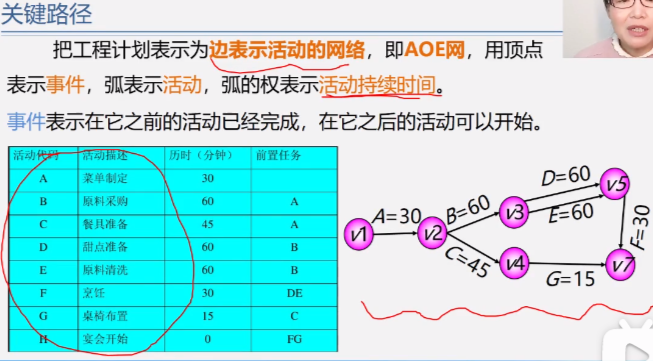
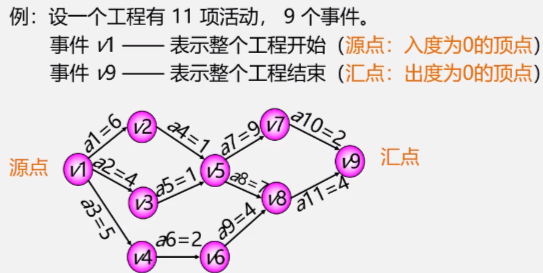
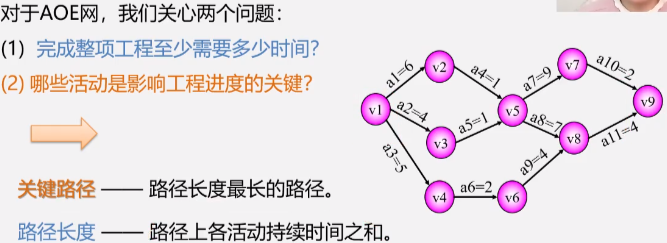
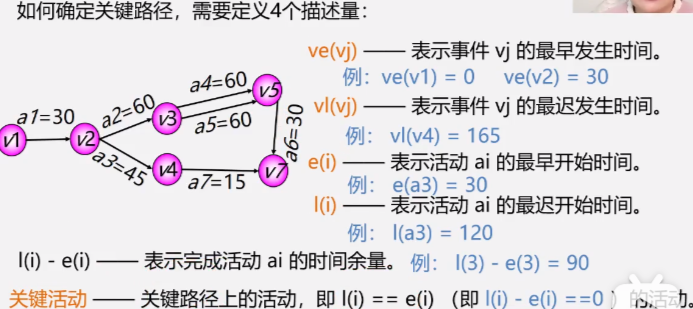
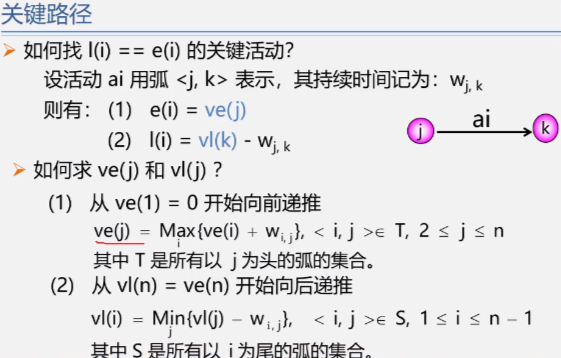
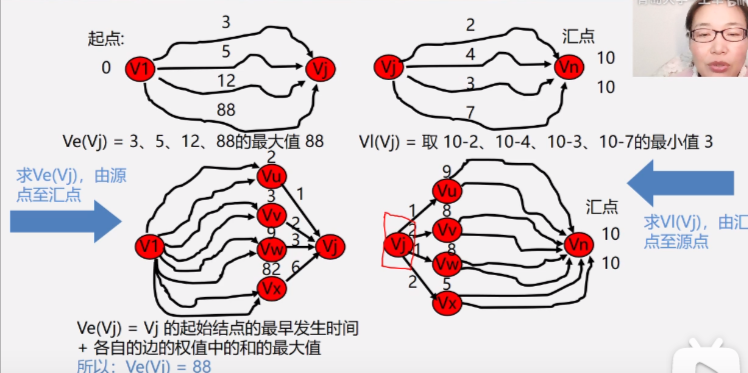
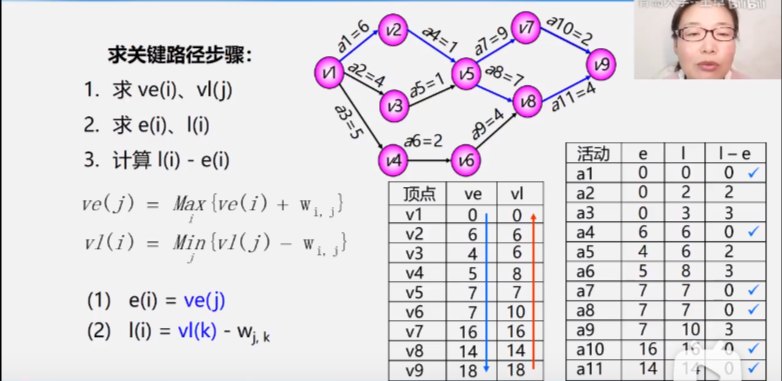
Therefore, the critical path can be shortened appropriately to reduce the time of the whole process, but not too much, otherwise the critical path will no longer be a critical path