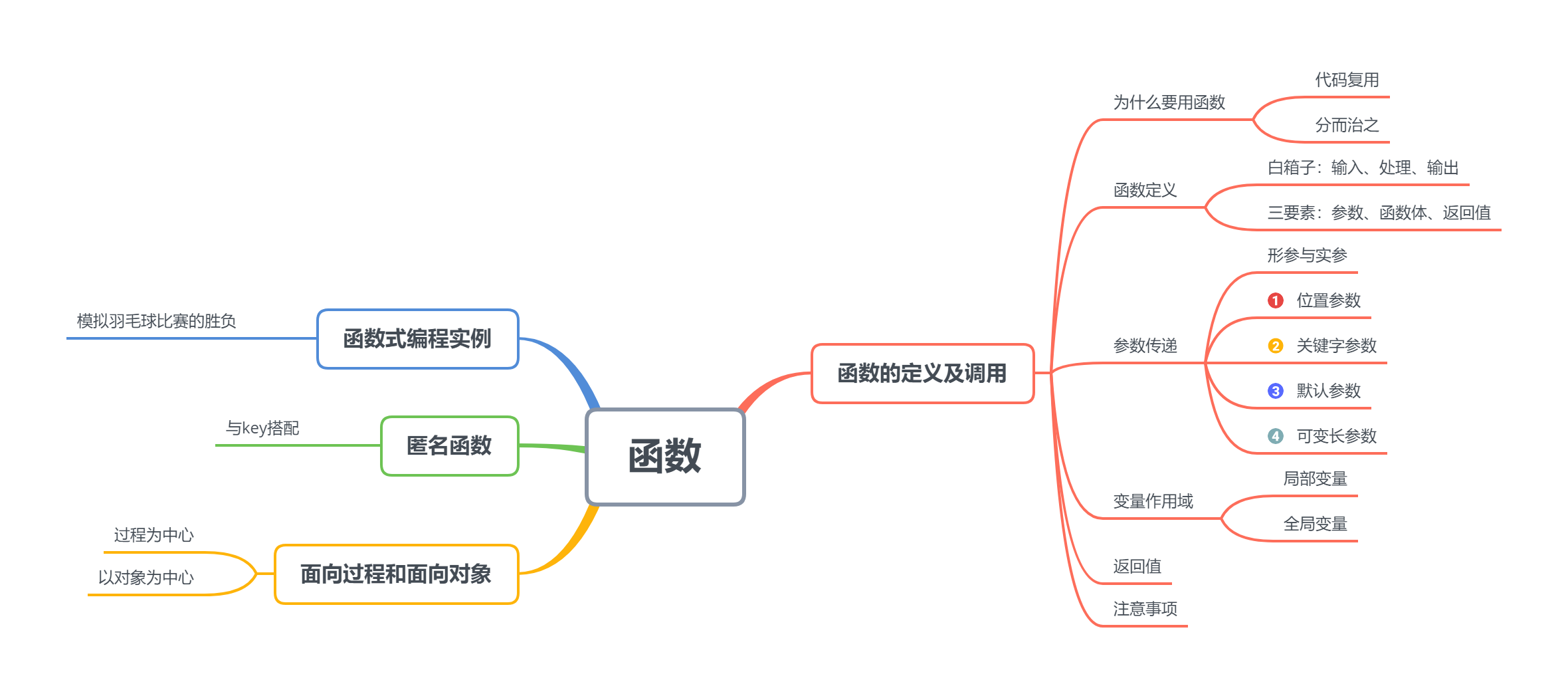
Chapter VI functions
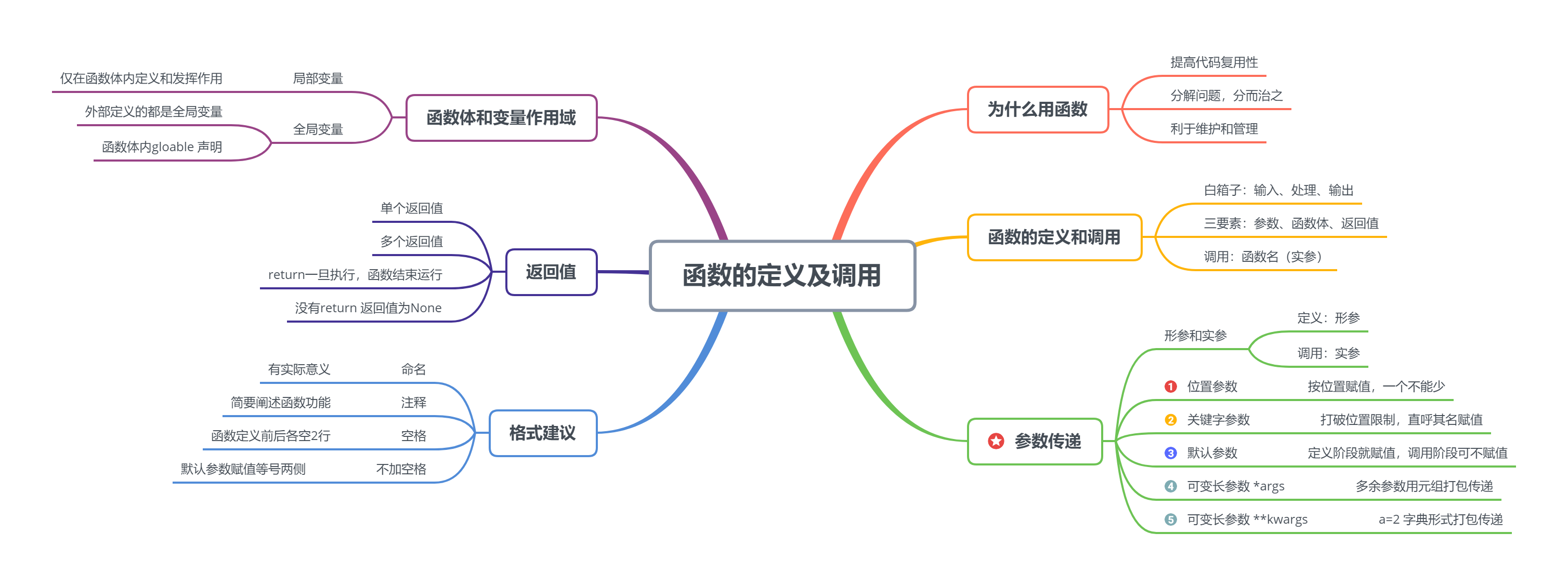
4.1 function definition and call
4.1.1 why to use function
1. Improve code reusability -- abstract and encapsulate as function
2. Decompose complex big problems into a series of small problems, divide and rule -- the idea of modular design
3. Facilitate code maintenance and management
Sequential form
# Factorial 5 n = 5 res = 1 for i in range(1, n+1): res *= i print(res) # Factorial 20 n = 20 res = 1 for i in range(1, n+1): res *= i print(res)
120 2432902008176640000
Abstract into function
def factoria(n): res = 1 for i in range(1,n+1): res *= i return res print(factoria(5)) print(factoria(20))
120 2432902008176640000
4.1.2 function definition and call
White box: input processing output
Three elements: parameter, function body and return value
1, definition
def function name (parameter):
function body
return return value
# Find the area of a square def area_of_square(length_of_side): square_area = pow(length_of_side, 2) return square_area
2. Call
Function name (parameter)
area = area_of_square(5) area
25
4.1.3 parameter transfer
0. Formal parameter and actual parameter
-
Parameter (formal parameter): the parameter when the function is defined, which is actually the variable name
-
Actual parameter (actual parameter): the parameter when the function is called, which is actually the value of the variable
1. Location parameters
-
To assign (Associate) parameters in strict order of position
-
Generally used when the parameters are relatively small
def function(x, y, z): print(x, y, z) function(1, 2, 3) # x = 1; y = 2; z = 3
1 2 3
- The number of actual parameters and formal parameters must correspond one by one, one cannot be more, one cannot be less
function(1, 2)
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-6-2a7da6ff9675> in <module> ----> 1 function(1, 2) TypeError: function() missing 1 required positional argument: 'z'
function(1, 2, 3, 4)
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-8-748d3d0335e6> in <module> ----> 1 function(1, 2, 3, 4) TypeError: function() takes 3 positional arguments but 4 were given
2. Key parameters
-
Break the position limit and call its name directly to pass the value (parameter = actual parameter)
-
One by one correspondence must be observed in the number of actual participating parameters
-
It is often used in the case of many parameters
def function(x, y, z): print(x, y, z) function(y=1, z=2, x=3) # x = 1; y = 2; z = 3
3 1 2
-
Location parameters can be mixed with key parameters
-
However, the location parameter must precede the key parameter
function(1, z=2, y=3)
1 3 2
function(1, 2, z=3)
1 2 3
- Cannot pass value repeatedly for the same parameter
def function(x, y, z): print(x, y, z) function(1, z=2, x=3)
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-12-f385272db011> in <module> 3 4 ----> 5 function(1, z=2, x=3) TypeError: function() got multiple values for argument 'x'
3. Default parameters
-
Assign a value to a parameter in the definition phase -- the common value of the parameter
-
Assign a value to a parameter in the definition phase -- the common value of the parameter
-
Default parameters must be placed after non default parameters
-
When calling a function, you can not pass a value to this parameter
-
The method of class in machine learning library is very common
def register(name, age, sex="male"): print(name, age, sex) register("Da Jie Zi", 18)
18 male
- You can also pass values according to normal parameters
register("Lin Chiling", 38, "female")
Lin Zhiling 38 female
- Default parameter should be set to immutable type (number, string, tuple)
def function(ls=[]): print(id(ls)) ls.append(1) print(id(ls)) print(ls) function()
1759752744328 1759752744328 [1]
function()
1759752744328 1759752744328 [1, 1]
function()
1759752744328 1759752744328 [1, 1, 1]
def function(ls="Python"): print(id(ls)) ls += "3.7" print(id(ls)) print(ls) function()
1759701700656 1759754352240 Python3.7
function()
1759701700656 1759754353328 Python3.7
function()
1759701700656 1759754354352 Python3.7
- Make parameters optional
def name(first_name, last_name, middle_name=None): if middle_name: return first_name+middle_name+last_name else: return first_name+last_name print(name("large","Child")) print(name("large", "Child", "Jie"))
Tsotsi Da Jie Zi
*4. Variable length parameter args
-
I don't know how many parameters * args will be passed
-
The parameter must be placed at the end of the parameter list
def foo(x, y, z, *args): print(x, y ,z) print(args) foo(1, 2, 3, 4, 5, 6) # Redundant parameters, packed and passed to args
1 2 3 (4, 5, 6)
- Dispersion of real evidence
def foo(x, y, z, *args): print(x, y ,z) print(args) foo(1, 2, 3, [4, 5, 6])
1 2 3 ([4, 5, 6],)
foo(1, 2, 3, *[4, 5, 6]) # A list, string, tuple, or collection is broken up
1 2 3 (4, 5, 6)
**5. Variable length parameter
def foo(x, y, z, **kwargs): print(x, y ,z) print(kwargs) foo(1, 2, 3, a=4, b=5, c=6) # Redundant parameters, packaged as dictionaries and passed to kwargs
1 2 3 {'a': 4, 'b': 5, 'c': 6}
- Dictionary argument break up
def foo(x, y, z, **kwargs): print(x, y ,z) print(kwargs) foo(1, 2, 3, **{"a": 4, "b": 5, "c":6})
1 2 3 {'a': 4, 'b': 5, 'c': 6}
- The combination of variable length parameters
def foo(*args, **kwargs): print(args) print(kwargs) foo(1, 2, 3, a=4, b=5, c=6)
(1, 2, 3) {'a': 4, 'b': 5, 'c': 6}
4.1.4 function body and variable scope
-
A function body is a piece of code that only executes when a function is called. The code structure is no different from other codes
-
Local variables - defined and functioning only within a function body
def multipy(x, y): z = x*y return z multipy(2, 9) print(z) # After the function is executed, the local variable z has been released
--------------------------------------------------------------------------- NameError Traceback (most recent call last) <ipython-input-29-9a7fd4c4c0a9> in <module> 5 6 multipy(2, 9) ----> 7 print(z) # After the function is executed, the local variable z has been released NameError: name 'z' is not defined
-
Global variables - External definitions are all global variables
-
Global variables can be used directly within a function body
n = 3 ls = [0] def multipy(x, y): z = n*x*y ls.append(z) return z print(multipy(2, 9)) ls
54 [0, 54]
- Defining global variables in function body through global
def multipy(x, y): global z z = x*y return z print(multipy(2, 9)) print(z)
18 18
4.1.5 return value
1. Single return value
def foo(x): return x**2 res = foo(10) res
100
2. Multiple return values -- in tuples
def foo(x): return 1, x, x**2, x**3 # Comma separated, pack return print(foo(3))
(1, 3, 9, 27)
a, b , c, d = foo(3) # Unpacking assignment print(a) print(b) print(c) print(d)
1 3 9 27
3. There can be multiple return statements. Once one of them is executed, it represents the end of function operation
def is_holiday(day): if day in ["Sunday", "Saturday"]: return "Is holiday" else: return "Not holiday" print("La demacia la la la la la la la") # You don't have a chance to run... print(is_holiday("Sunday")) print(is_holiday("Monday"))
Is holiday Not holiday
4. No return statement, return value is None
def foo(): print("I'm Monkey King") res = foo() print(res)
I'm Monkey King None
4.1.6 suggestions
1. Naming of functions and their parameters naming of reference variables
-
Combination of lowercase and underline
-
Practical significance
2. It should include comments that briefly describe the function functions, followed by the function definition
def foo(): # The purpose of this function is to show you, what do you see, how do you.... pass
3. Two blank lines before and after function definition
def f1(): pass # Empty two lines to show innocence def f2(): pass def f3(x=3): # No space is required on both sides of equal sign of default parameter assignment pass # ...
4. No space is required on both sides of equal sign of default parameter assignment
4.2 example of functional programming
Modular programming idea
- Divide and rule from top to bottom
[problem description]
-
Xiaodan and Xiaowei play badminton well, and their level is also between Bo Zhong. Xiaodan is a little better. Basically, playing 100 balls, Xiaodan can win 55 times, and Xiaowei can win 45 times.
-
But every time in a big game (the winner is determined in the first set, who wins 21 points first, who wins), Xiaodan's probability of winning is far greater than Xiaowei, Xiaowei is very unconvinced.
-
Dear friends, can you reveal the mystery through simulation experiments?
[problem abstraction]
1. In Xiaodan Vs Xiaowei's binary game system, Xiaodan has a 55% winning probability per ball and Xiaowei has a 45% winning probability per ball;
2. In each game, whoever wins 21 goals (21 points) first wins;
3. Assuming an independent game of n = 10000, how many games will Xiao Dan win? (when n is large, the experimental result is about the real expectation)
[problem decomposition]
def main(): # Main logic prob_A, prob_B, number_of_games = get_inputs() # Get raw data win_A, win_B = sim_n_games(prob_A, prob_B, number_of_games) # Get simulation results print_summary(win_A, win_B, number_of_games) # Result summary output
1. Input raw data
def get_inputs(): # Input raw data prob_A = eval(input("Please enter athletes A Win probability per ball of(0~1): ")) prob_B = round(1-prob_A, 2) number_of_games = eval(input("Please enter the number of analog fields (positive integer):")) print("Total number of simulation competitions:", number_of_games) print("A Winning probability of each ball:", prob_A) print("B Winning probability of each ball:", prob_B) return prob_A, prob_B, number_of_games
Unit test
prob_A, prob_B, number_of_games = get_inputs() print(prob_A, prob_B, number_of_games)
Please input player A's winning probability per ball (0-1): 0.55 Please input the number of simulated fields (positive integer): 10000 Total number of simulation competitions: 10000 Player A's winning probability per ball: 0.55 Player B's winning probability per ball: 0.45 0.55 0.45 10000
2. Multiple game simulation
def sim_n_games(prob_A, prob_B, number_of_games): # Simulate the results of multiple games win_A, win_B = 0, 0 # Initialize the winning matches of A and B for i in range(number_of_games): # Number of iterations score_A, score_B = sim_one_game(prob_A, prob_B) # Get the score of the simulation match in turn if score_A > score_B: win_A += 1 else: win_B += 1 return win_A, win_B
import random def sim_one_game(prob_A, prob_B): # Simulate the outcome of a game score_A, score_B = 0, 0 while not game_over(score_A, score_B): if random.random() < prob_A: # random.random() produces random decimals between [0,1], evenly distributed score_A += 1 else: score_B += 1 return score_A, score_B
def game_over(score_A, score_B): # The end condition of single simulation: one side reaches 21 points first, and the game is over return score_A == 21 or score_B == 21
assert for unit test -- assertion
-
assert expression
-
Trigger exception when expression result is false
assert game_over(21, 8) == True assert game_over(9, 21) == True assert game_over(11, 8) == False assert game_over(21, 8) == False
--------------------------------------------------------------------------- AssertionError Traceback (most recent call last) <ipython-input-42-88b651626036> in <module> 2 assert game_over(9, 21) == True 3 assert game_over(11, 8) == False ----> 4 assert game_over(21, 8) == False AssertionError:
print(sim_one_game(0.55, 0.45)) print(sim_one_game(0.7, 0.3)) print(sim_one_game(0.2, 0.8))
(21, 7) (21, 14) (10, 21)
print(sim_n_games(0.55, 0.45, 1000))
(731, 269)
3. Result summary output
def print_summary(win_A, win_B, number_of_games): # Result summary output print("Co simulation{}Match".format(number_of_games)) print("Player A Win victory{0}Field ratio{1:.1%}".format(win_A, win_A/number_of_games)) print("Player B Win victory{0}Field ratio{1:.1%}".format(win_B, win_B/number_of_games))
print_summary(729, 271, 1000)
1000 games simulated Player A won 729 games, accounting for 72.9% Player B won 271 games, accounting for 27.1%
import random def get_inputs(): # Input raw data prob_A = eval(input("Please enter athletes A Win probability per ball of(0~1): ")) prob_B = round(1-prob_A, 2) number_of_games = eval(input("Please enter the number of analog fields (positive integer):")) print("Total number of simulation competitions:", number_of_games) print("A Winning probability of each ball:", prob_A) print("B Winning probability of each ball:", prob_B) return prob_A, prob_B, number_of_games def game_over(score_A, score_B): # The end condition of single simulation: one side reaches 21 points first, and the game is over return score_A == 21 or score_B == 21 def sim_one_game(prob_A, prob_B): # Simulate the outcome of a game score_A, score_B = 0, 0 while not game_over(score_A, score_B): if random.random() < prob_A: # random.random() produces random decimals between [0,1], evenly distributed score_A += 1 else: score_B += 1 return score_A, score_B def sim_n_games(prob_A, prob_B, number_of_games): # Simulate the results of multiple games win_A, win_B = 0, 0 # Initialize the winning matches of A and B for i in range(number_of_games): # Number of iterations score_A, score_B = sim_one_game(prob_A, prob_B) # Get the score of the simulation match in turn if score_A > score_B: win_A += 1 else: win_B += 1 return win_A, win_B def print_summary(win_A, win_B, number_of_games): # Result summary output print("Co simulation{}Match".format(number_of_games)) print("\033[31m Player A Win victory{0}Field ratio{1:.1%}".format(win_A, win_A/number_of_games)) print("Player B Win victory{0}Field ratio{1:.1%}".format(win_B, win_B/number_of_games)) def main(): # Main logic prob_A, prob_B, number_of_games = get_inputs() # Get raw data win_A, win_B = sim_n_games(prob_A, prob_B, number_of_games) # Get simulation results print_summary(win_A, win_B, number_of_games) # Result summary output if __name__ == "__main__": main()
Please input player A's winning probability per ball (0-1): 0.52 Please input the number of simulated fields (positive integer): 10000 Total number of simulation competitions: 10000 Player A's winning probability per ball: 0.52 Player B's winning probability per ball: 0.48 10000 games simulated [31m player A won 6033 games, accounting for 60.3% Player B won 3967 games, accounting for 39.7%
According to statistics, Xiaodan and Xiaowei have played 40 times in 14 years. Xiaodan leads by 28:12.
Among them, the two engaged in a total of 100 rounds:
Xiaodan won 61 games, accounting for 61%;
Xiaowei won 39 games, accounting for 39%.
You think the gap between you and others is just a little. Actually, the gap is big
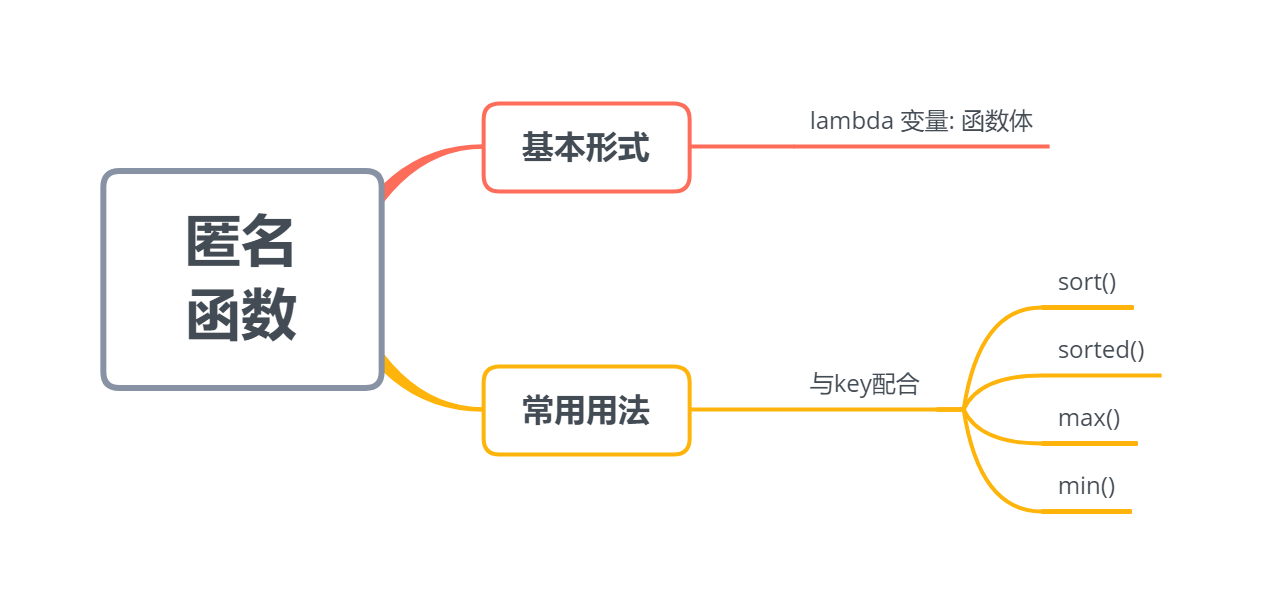
4.3 anonymous functions
1. Basic form
lambda variables: function bodies
2. Common usage
Anonymous functions are best used in parameter lists, especially with key =
- Sort() sorted()
ls = [(93, 88), (79, 100), (86, 71), (85, 85), (76, 94)] ls.sort() ls
[(76, 94), (79, 100), (85, 85), (86, 71), (93, 88)]
ls.sort(key = lambda x: x[1]) ls
[(86, 71), (85, 85), (93, 88), (76, 94), (79, 100)]
ls = [(93, 88), (79, 100), (86, 71), (85, 85), (76, 94)] temp = sorted(ls, key = lambda x: x[0]+x[1], reverse=True) temp
[(93, 88), (79, 100), (85, 85), (76, 94), (86, 71)]
- max() min()
ls = [(93, 88), (79, 100), (86, 71), (85, 85), (76, 94)] n = max(ls, key = lambda x: x[1]) n
(79, 100)
n = min(ls, key = lambda x: x[1]) n
(86, 71)
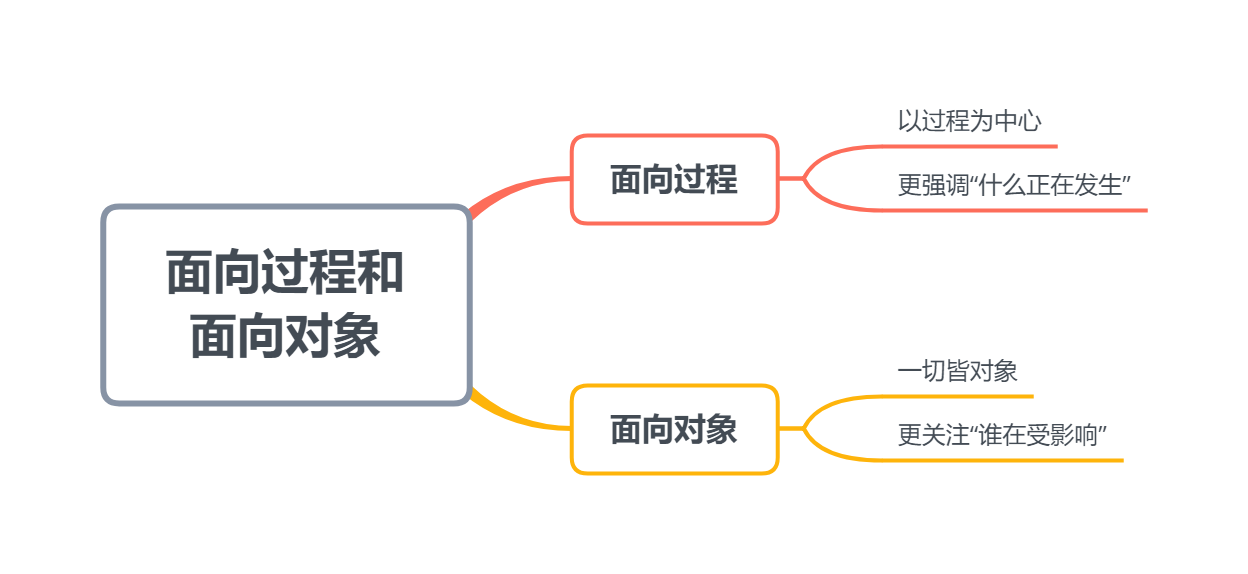
4.4 process and object oriented
Process oriented -- process centered programming idea, with "what is happening" as the main goal of programming. Cold, programmed
Object oriented: abstract things in the real world into objects, pay more attention to "who is affected" and be closer to reality. Flesh and blood, anthropomorphic
- Take the bus as an example
"Process oriented": car start is one event, car arrival is another event....
When programming, we are concerned with an event, not the car itself.
We write programs for startup and arrival respectively.
"Object oriented": construct the object of "car".
The object includes a series of "attributes" such as power, service time, manufacturer, etc;
It also includes a series of "methods" such as refueling, starting, acceleration, braking, turning, honking, arrival, maintenance, etc.
Express corresponding events through the behavior of objects