lookup

The definition of search is the process of finding the element with keyword k in the data structure storing several elements. If the table is modified during the lookup process, it is called a dynamic lookup table, otherwise it is a static lookup table.

PI is the probability of finding the ith element in the table, ci is the number of keyword comparisons required to find the ith element in the table, and ASL is defined= Σ (pi*ci) is the average search length of successful search. Similarly, there is the average search length of failed search.

The larger the ASL value of the search algorithm, the worse the time performance. On the contrary, the better the time performance.

Linear table lookup

As the name suggests, it is to look up in a linear table.

Sequential search

This code will not be demonstrated. Sequential search is to traverse all elements until the end of the element with the same value as the searched value. This is also the simplest search.

For the first element, you can find it once from beginning to end, for the second element, you can find it twice from beginning to end... For the X element, you can find it x times from beginning to end, that is, ci=i. So ASL=1/n*(1+2 ···· + n)=(1+n)/2.

If the lookup value is not in the table, it needs to be compared n times to judge the lookup failure, so ASL (failure) = n.

Half search

It is binary search. Look at the concepts and many variants of binary search This article , the most basic code provided here will not be repeated.

int Binary_Search(int*a,int target,int l,int r){//l and r respectively represent the left and right endpoints of the search interval for each half search
	while (l<r){int mid=l+(r-l)/2;//Find the midpoint 
		if (a[min]==target) return m;//If it is found, return directly. If it is not found, choose to continue to find the left half or the right half 
		//Because it is a monotone sequence, when the middle value is greater than the value we are looking for, it means that we don't need to consider the sequence on the right half
		//Similarly, when the middle value is less than the value we are looking for, it means that we don't need to consider the sequence of the left half
		else if (a[min]>target) r=mid-1; else l=mid+1; 
	} return -1;//Can't find 
}

Binary search is used to find the node of each search, and the search interval is divided into two intervals to obtain a binary tree similar to the segment tree:

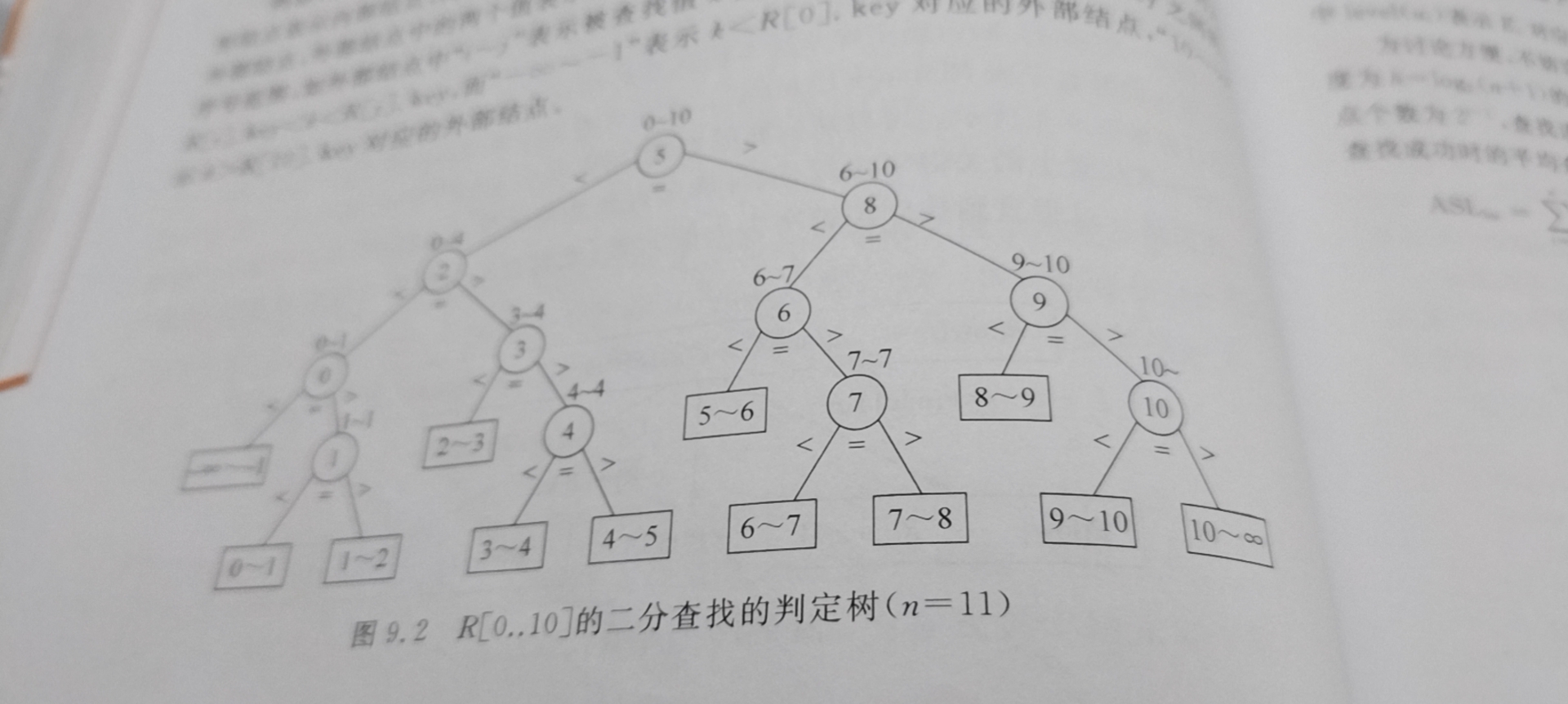
ASL (successful)= Σ (pi * the depth of the ith node in the binary tree), there is little difference between the failure of the search and the number of successful comparisons, and the time complexity is O(logn).

Index storage structure and block lookup

Index storage structure

Index storage structure is to define the address of an index table in the data table when storing data. For example, the following figure:

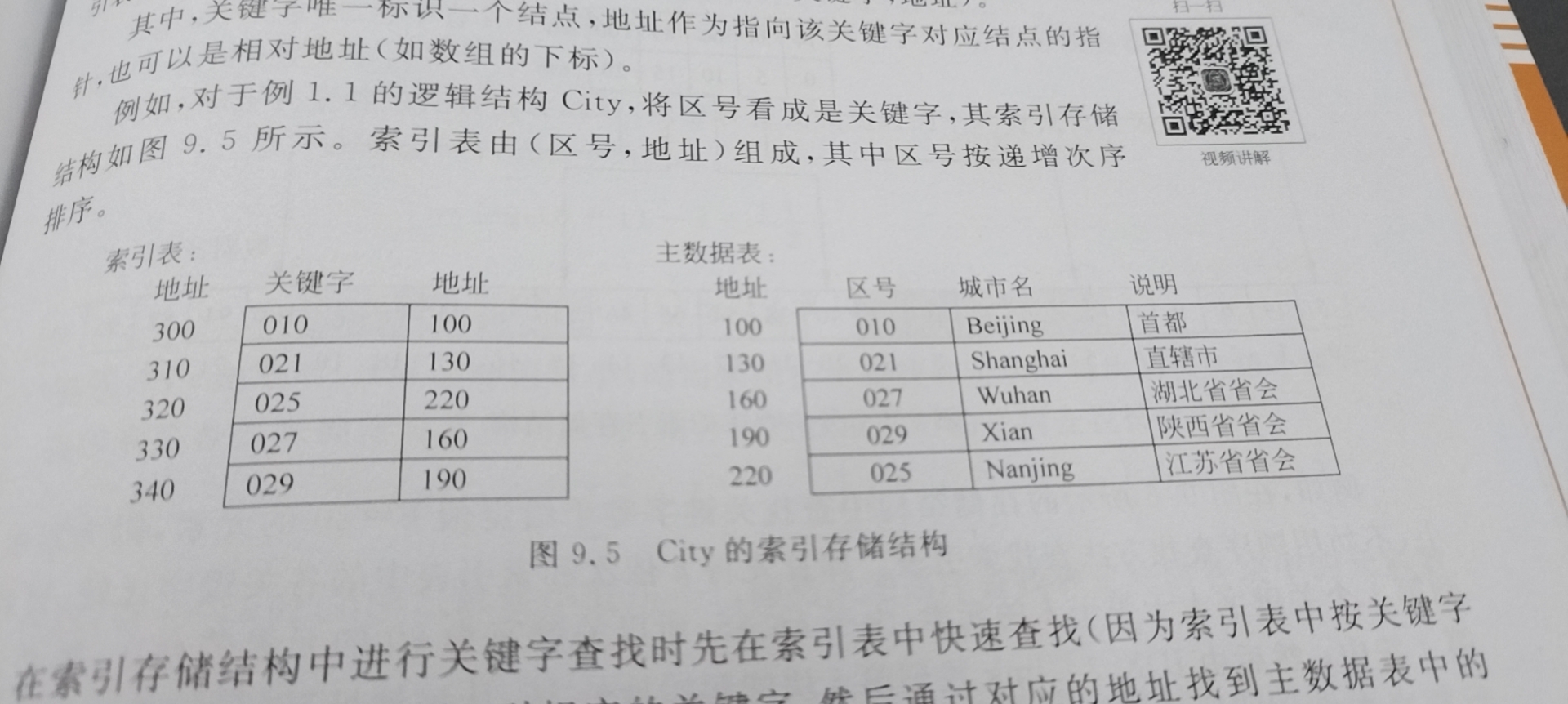
The keywords in the index table are arranged in order. When searching for keywords, first perform a binary search in the index table to find the corresponding address (index), and then find the elements in the main data table according to the address.

(in fact, I don't know why I don't directly convert the master data table into an ordered table if keywords can be sorted. The reason I can think of is that the master data table can't be modified at will).

Block search

Block search is a search method between sequential search and binary search. It does not need to completely convert the table into an ordered table. The table is equally divided into B blocks. The number of elements in the first b-1 block is rounded up by the number of elements n/b. the keywords in each block do not need to meet the order, but the maximum keyword of the previous block must be less than the minimum keyword of the latter block.

Suppose there are n elements in a linear table that meet the above conditions, divide it into x blocks according to the above rules, and take the largest element in each block and the subscript (address) of the first element in the block to build an index table. The examples in the book are as follows:

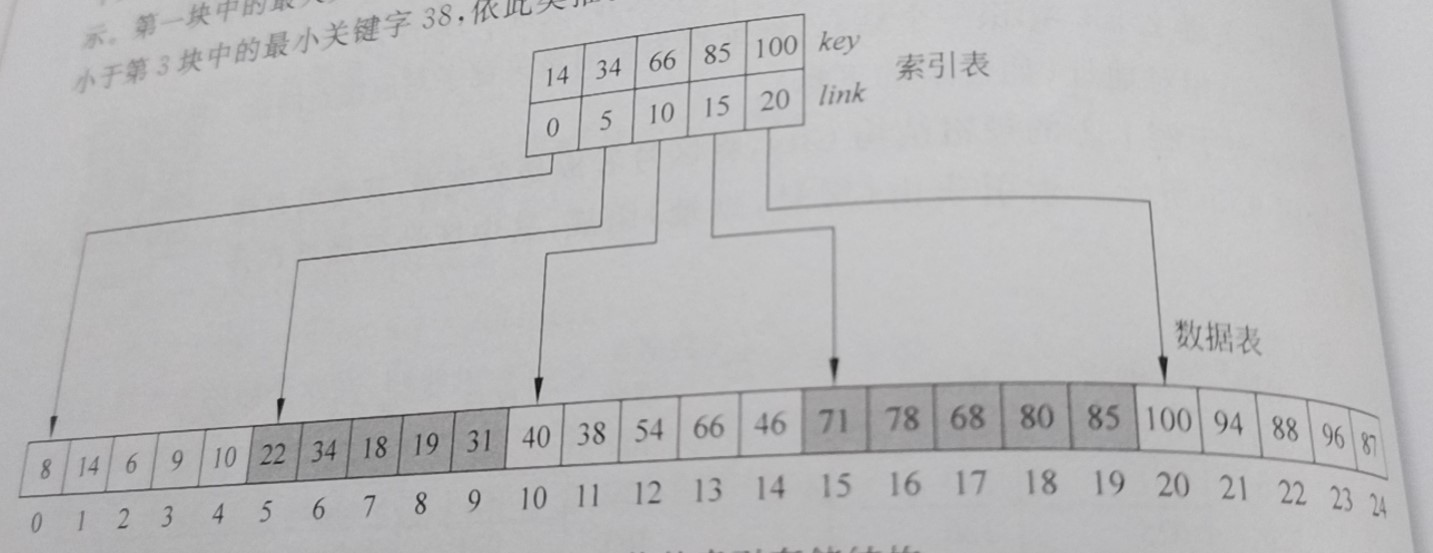
When we want to find a keyword, we first find it in the index table to determine the blocks to be found in the data table. For example, if the element to be searched is 80, and 80 is greater than 66 and less than 85, it means that the subscript of element 80 in the data table is 15-19, and then the sequential search is carried out in the blocks of 15-19.

struct RecType{KeyType key;	InfoType data;};//key is the keyword, data is other data, and RecType is the data type in the table		
struct IdxType{KeyType key; int link;};//key is the largest element of the corresponding block, and link is the starting subscript of the corresponding block 
//For block search, I is the index table, b is the length of the index table, R is the main data table, n is the total number of elements, and k is the search value 
int IdxSearch(IdxType I[],int b,RecType R[],int n,KeyType k){	
	int s=(n+b-1)/b;//s is the number of elements in each block, which should be rounded up by n/b
	int low=0,high=b-1,mid;
	//Perform binary search to find the blocks that need to be searched in sequence, and the block subscript is high+1 
	while (low<=high){mid=(low+high)/2;
		if (I[mid].key>=k) high=mid-1; else low=mid+1;
	}
	int i=I[high+1].link;
	while (i<=I[high+1].link+s-1&&R[i].key!=k) i++;//Perform sequential lookup 
	if (i<=I[high+1].link+s-1) return i+1; else return 0;//Here is the return logical number, not the subscript, and + 1 is required		
}

ASL = ASL (binary search) + ASL (sequential search) = log([n/s]+1)+s/2.

When the partition is determined by binary search, the smaller s, the smaller ASL value; When using sequential search to determine the block where the element is located, when s=sqrt(n), the ASL value is basically the smallest.

It can be seen that the number of elements in blocks can determine whether they prefer binary search or sequential search. The fewer the number of elements in blocks, the more inclined they are to binary search. When the number of elements in each block is 1, it will directly change to binary search. When the number of elements in blocks is n, it will retreat to sequential search.