Basic concepts of binary trees

Binary trees are similar to quadratic trees, but differ slightly from quadratic trees:

A tree with a degree of 2 has at least one node with a degree of 2, which is not required for a binary tree. In short, a binary tree can degenerate into a chain.

2. Trees with 2 degrees can distinguish left from right subtrees, and the order of left and right subtrees (nodes) in a binary tree can strictly distinguish the arrangement.

The basic terms of Man Binary Tree are the same as those of Tree, and so are the logical expressions and Trees. In addition to these are:

Such a binary tree is called a complete binary tree if at most only the nodes in the bottom two layers can have less than 2 degrees, and the nodes of the leaves in the bottom two layers are arranged sequentially in the leftmost position of the layer.

A complete binary tree can also be defined as a binary tree with a depth of k and n nodes, numbering the nodes in the tree in order from top to bottom and from left to right. If a node numbered i is in the same position as a node numbered i in a full binary tree, the binary tree is called a complete binary tree.

Non-empty complete binary trees are characterized by the following:

1. Leaf nodes may only appear in the bottom two layers (definitions).

2. For leaf nodes in the largest hierarchy, they are sequentially arranged (defined) on the leftmost side of the layer.

3. If there is a degree 1 node, only one may appear, and the node has only a left child but no right child (this node is the parent node of the rightmost node in the largest hierarchy).

4. Number in sequence, once the node numbered i is a leaf node or has only a left child, all nodes numbered greater than i are leaf nodes (essentially the same as property 3).

5. When the number of nodes n is even, the number of the lowest nodes is odd. There is a single branch node for the whole tree species, otherwise it is even and there is no single branch node.

Properties of Binary Trees

1. The number of leaf nodes of a binary tree is equal to the number of double branch nodes + 1.

The number of leaf nodes is counted as x, the number of single branch nodes as y, and the number of double branch nodes as Z. By the nature of the tree 1, the number of nodes in the tree = degree + 1 of all nodes, there are: x+y+z=y+2*z+1, simplified as x=z+1.

Properties 2 and 3 are properties 2 and 3 of a tree.

4. Nodes with sequence number i in a complete binary tree have the following properties:

4.1 If 2i<=n, the node numbered I is the branch node.

The number of leaf nodes is equal to the number of branch nodes or the number of branch nodes + 1. This conclusion is very obvious because we know from property 1 that the number of leaf nodes of a binary tree is equal to the number of double-branch nodes + 1, and then we know from the feature 5 of a complete binary tree that when n is even, there is a single-branch node, where the total number of branch nodes = 1 + double-branch nodes = single-branch nodes + double-branch nodes, i=n/2.

The conclusion that the same n is odd can be similarly proved.

Conclusion 4.2 is the combination of feature 5 and property 4.1 above.

4.3 If the node numbered I has a left child node, the number of the left child node is 2i, and if there is a right child node, the number of the right child node is 2i+1.

Set the depth of I to x, that is, 2x-1 < < I < < 2x-1, the nodes before the same level node i have i-2x-1+1, each node has two children, so there are 2x-1+2*(i-2x-1+1)=2i-1 before the node i children node. So the number of the left child is 2i-1+1=2i, and the number of the right child is 2i+1.

4.4 In addition to the root node, if a node is numbered i, its parent node is numbered i/2 rounded down.

And 4.3 are twin theorems.

5. A complete binary tree with n nodes is rounded up by log2(n+1) or down by log2(n+1).

Conversion between Binary Tree and Tree, Forest

Trees, forests and binary trees have a relationship of transformation, that is, any forest or tree can uniquely correspond to a binary tree in some way, and binary trees can also uniquely correspond to a forest or a tree.

Convert Tree to Binary Tree

Let's take the following tree as an example:

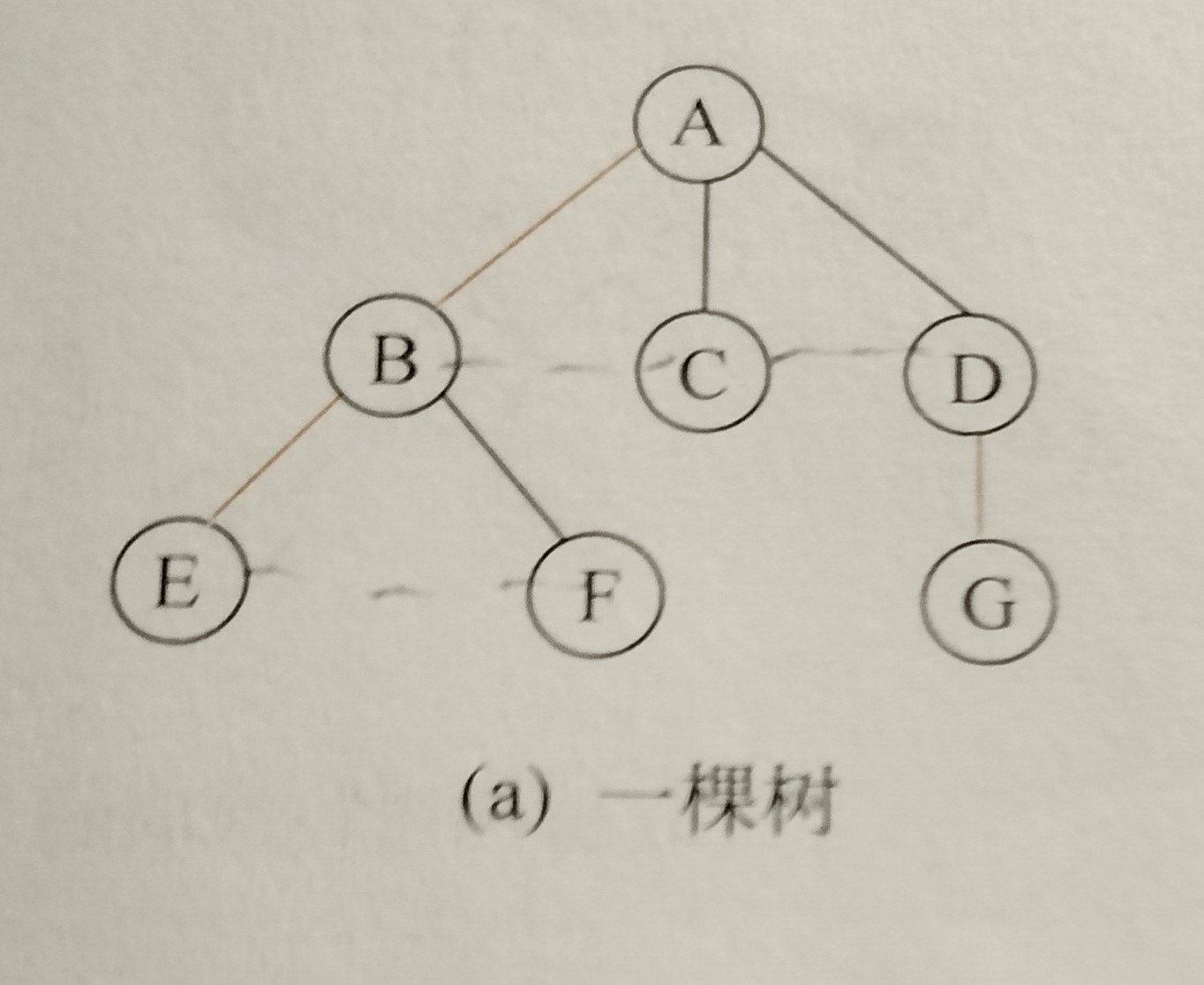
1. Add a line between the adjacent sibling nodes in the book. Note that the adjacent siblings are not nodes of the same layer. For example, node E and node F below need a line, node F and node G do not.

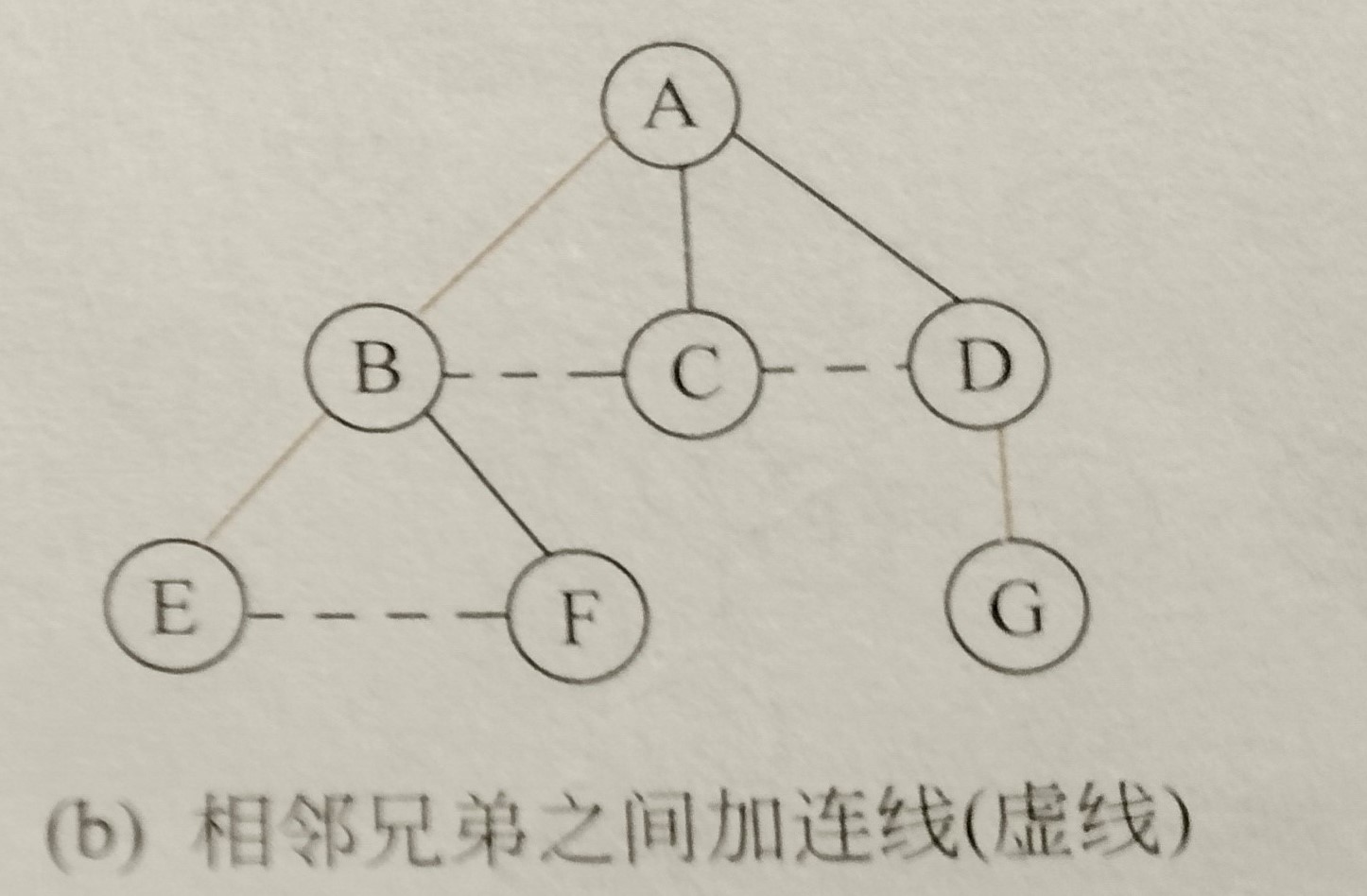
2. For each node in the tree, only the connection between it and the long child is preserved, and the connection with other children's nodes is deleted.

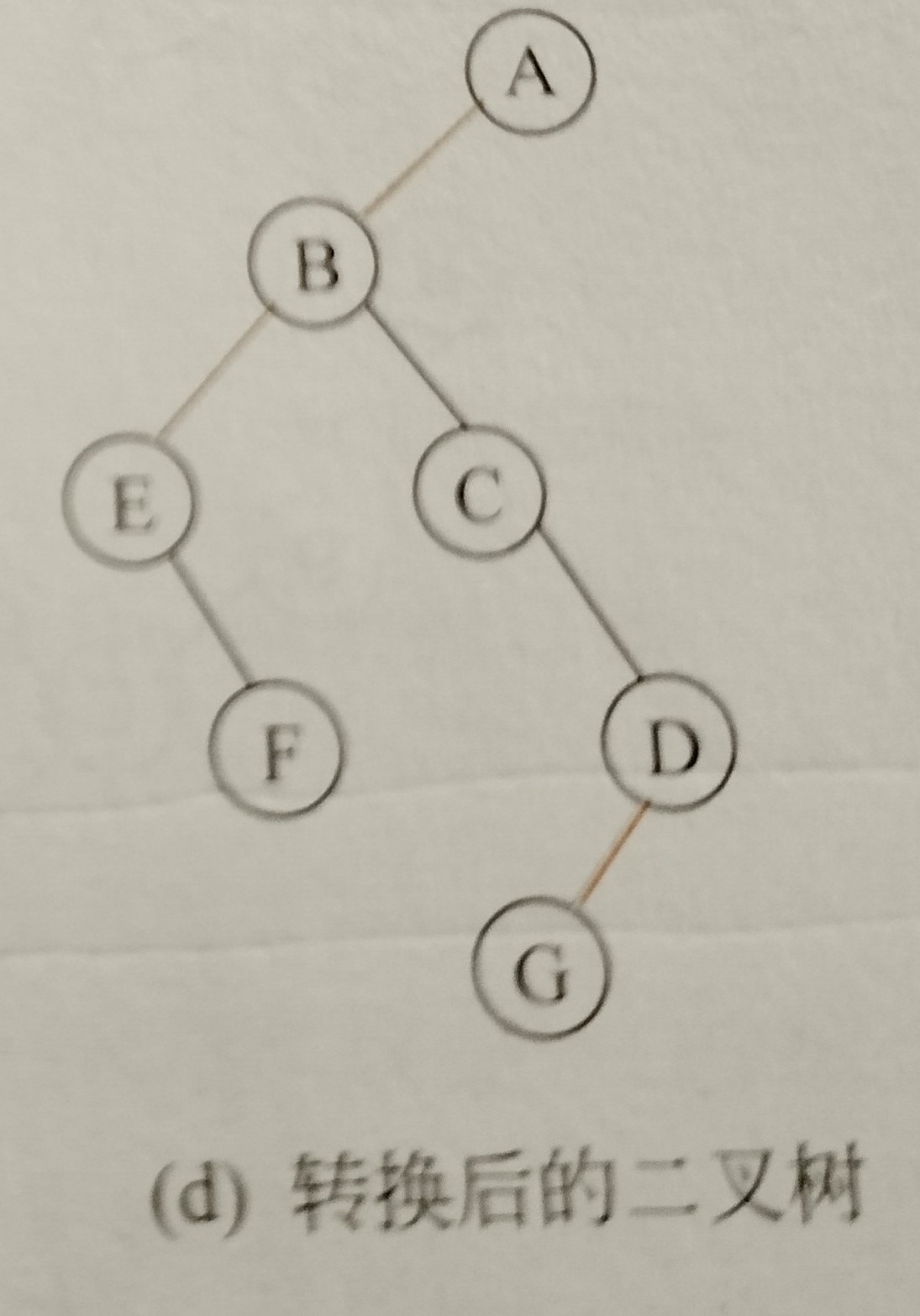
By this time the whole tree has been transformed into a binary tree with the root node of the original tree as its root node. For a node, if it has a sibling node, the sibling node is its right child node, and if it has a child node, the remaining elder child node is its left child node. The adjusted structure is as follows:

Converting forests to binary trees

1. First convert each tree in the forest into a binary tree.

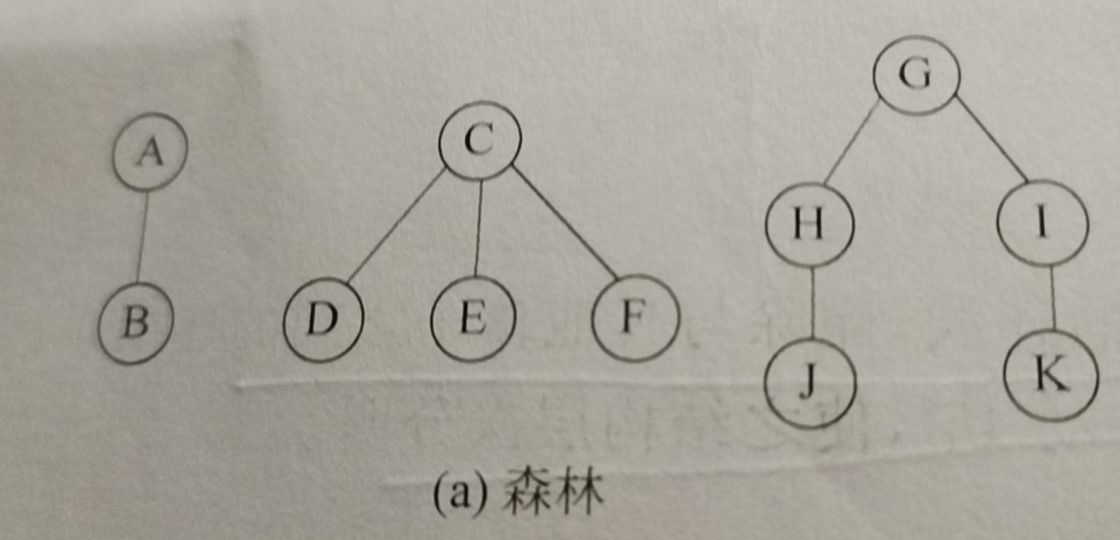
(converted binary tree)

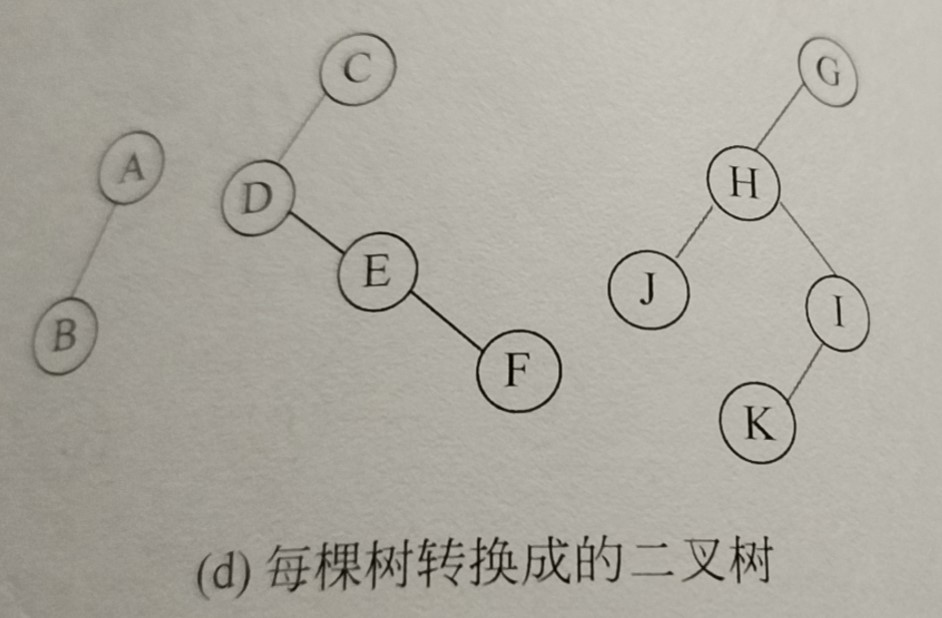
2. From the second binary tree, use the root node of the latter binary tree as the right child node of the root node of the previous binary tree, that is, the latter binary tree as the right subtree of the previous binary tree.

The transformation from tree to binary tree shows that for the top root node, only the leftmost child node is transformed into the left child node, and there is no sibling node for the root node, so the position of the right child node of the root node must be empty. So you can insert the latter binary tree into the position of the right child node of the root node of the previous binary tree.

The converted results are as follows:

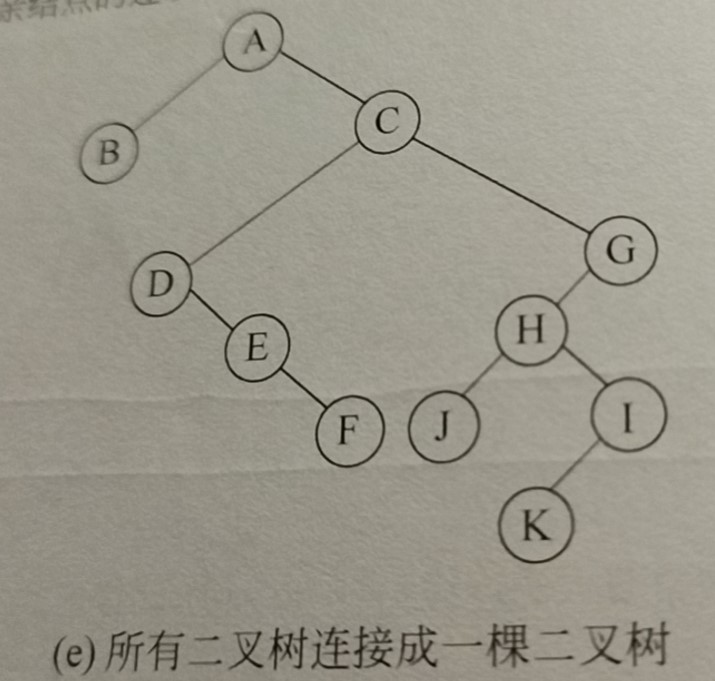
Binary Tree Restored to Tree

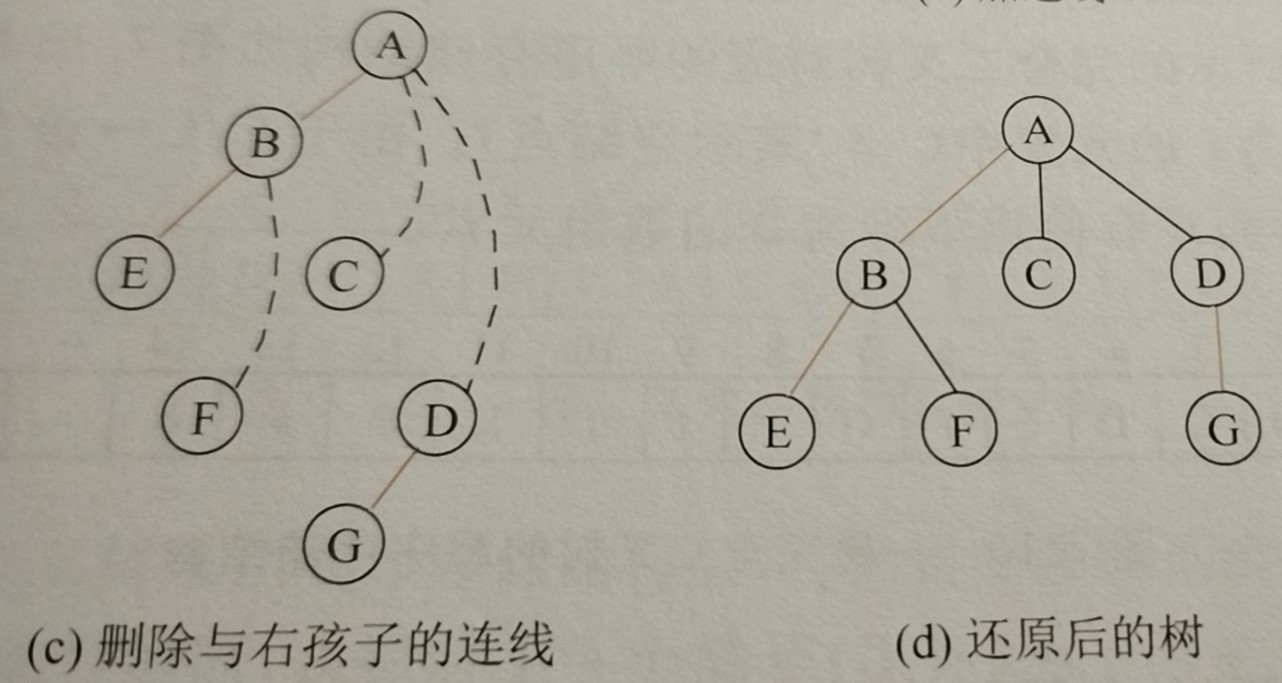
Reverse the steps from tree to binary tree to tree restoration, and you can imagine that the first step is to reconnect the root node of a tree to a child node other than its first child. From the process of transforming a tree into a binary tree, we can know that the first step is to use the long-child node as the left child node of the root of the binary tree, the child node adjacent to the long-child node, the right child node of the long-child node, and the right child node of the right-child node.

1. If a node is the left child of the starting parents, the right child of the node, the right child of the right child, etc. are connected to the parent node of the node.

The next step is to break the link between the adjacent nodes in the original tree, that is, the link between the root node and the right child node in the transformed binary tree.

2. Delete and adjust all parent-to-right child connections in the original binary tree.

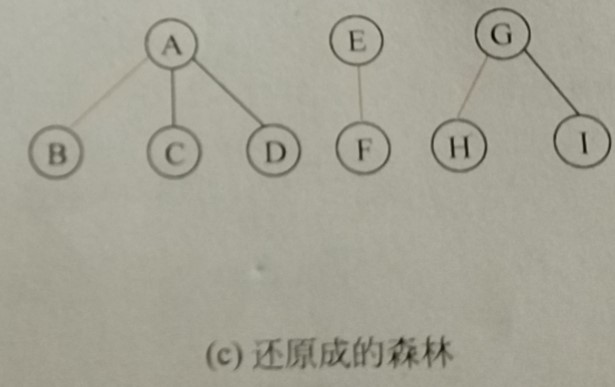
Binary Tree Restored to Forest

The process of converting a forest into a binary tree is to insert each converted binary tree into the position of the right subnode of the previous binary tree. That is, for a binary tree to be restored to a forest, the root node of the binary tree and the number of all right children (that is, right children and right children) are m, and the number of trees in the converted forest is m.

1. For a binary tree with a root node and the number of all right children of m, we divide the right subtree of the current binary tree one at a time and divide it m times.

2. Convert these binary trees into trees.

Binary Tree Storage Structure (Chain)

Sequential storage structures can also store binary trees, such as full and full binary trees. Sequential storage structures are very good storage methods. Processing binary tree codes in sequential storage structures is very simple and efficient.

However, for the vast majority of binary trees, using sequential storage structure, many empty nodes are required to construct a binary tree into a complete binary tree. The worst case is that the binary tree degenerates into a chain, and all the nodes of the left subtree need to be filled, so the space waste is very serious.

Therefore, a chain storage structure is generally considered for ordinary binary trees.

data stores values, lchild points to left child, rchild points to right child

//lchild points to left child node, rchild points to right child node 
struct BTNode{ElemType data; BTNode *lchild; BTNode *rchild;};

You can add another parent pointer to the parent node.

Create Binary Tree

The binary tree string str denoted by parentheses is created as a binary tree, basically the same as the child chain storage structure. Use a stack to store the root node containing the child nodes, traversing all the characters of the string:

//Creating Binary Trees from Bracket Expressions str 
void CreateBTree(BTNode * &b,char *str){
	BTNode *St[MaxSize],*p=NULL;//St is the stack that stores parent nodes with child nodes, top is the top of the stack, and the new node is the child node of the top of the stack node 
	int top=-1,k,j=0; char ch;//k is used to identify whether the current traversed child node is a left or a right child node, 1 left and 2 right 
	b=NULL;	ch=str[j]; 
	while (ch!='\0'){
   	   	switch(ch){//If the left half bracket indicates that the current node has a child node, put the node on the stack, the first child node must be the left child node, k=1 
		case '(':top++; St[top]=p; k=1; break; 
		case ')':top--; break;//The subtree of the top node of the stack traverses completely, leaving the stack 
		case ',':k=2; break;//A comma is encountered indicating that there is a new child node, which is the right child node, k=2 
		default:p=(BTNode *)malloc(sizeof(BTNode));//Encountered a character indicating a new node, allocating space and assigning values to the node 
				p->data=ch; p->lchild=p->rchild=NULL;
				if (b==NULL) b=p;//The first character encountered is the root node
				else{//The current node is a child of the top node of the stack, establishing a pointer from the root node to the child node	
					switch(k){//Determine whether it is a left or right child node based on k 
						case 1: St[top]->lchild=p; break;
						case 2: St[top]->rchild=p; break;
					}
				}
		}j++; ch=str[j];
	}
}

Output Binary Tree

Basically the same as the previous section:

//Output Binary Tree
void DispBTree(BTNode *b){
	if (b!=NULL){printf("%c",b->data);//Print Root Node 
		if (b->lchild!=NULL||b->rchild!=NULL){//Nodes with children print brackets, and subtrees with left and right recursively 
			printf("("); DispBTree(b->lchild);//Print left parenthesis, recursively print left subtree				
			if (b->rchild!=NULL) printf(",");//Output only when there is a right child node,
			DispBTree(b->rchild); printf(")");//Recursively print right subtree, print right half bracket					
		}
	}
}

Destroy Binary Tree

First destroy the left and right subtrees down, then the root node:

//Destroy Binary Tree
void DestroyBTree(BTNode *&b){
	if (b!=NULL){//First destroy the left and right subtrees, then the root node	
		DestroyBTree(b->lchild); DestroyBTree(b->rchild); free(b);
	}
}

Find Nodes

In a binary tree with b as the root node, find the node whose element value is x. The search process is to find the root node first, then the left subtree, then the right subtree.

//Find Nodes
BTNode *FindNode(BTNode *b,ElemType x) {BTNode *p;
	if (b==NULL) return NULL;//b is empty, abandon search 
	else if (b->data==x) return b;//Find the root node whose value is x and return b 
	else{p=FindNode(b->lchild,x);//Find left subtree 
		if (p!=NULL) return p;//The left subtree has a node P with the value x, returning p 
		else return FindNode(b->rchild,x);//Otherwise, find the right subtree 
	}
}

Find Children Node

Just access it directly from the pointer:

//Find Left Child Node 
BTNode *LchildNode(BTNode *p){return p->lchild;}
//Find Right Child Node 
BTNode *RchildNode(BTNode *p){return p->rchild;} 

Finding the Height of a Binary Tree

This is the same as a normal tree, where the depth of the tree with the current node as the root node is equal to the maximum of + 1 of the depth of the subtree with the root node, and returns a depth of 0 when an empty tree is encountered.

//Finding the Height of a Binary Tree 
int BTHeight(BTNode *b) {int lchildh,rchildh;//lchildh is the height of the left subtree and rchildh is the height of the right subtree 
	if (b==NULL) return(0);//Empty tree height returns 0
	else{//Finding the Height of Left and Right Subtrees 
		lchildh=BTHeight(b->lchild); rchildh=BTHeight(b->rchild);
		return (lchildh>rchildh)?(lchildh+1):(rchildh+1);//The current tree height is the maximum height of the left and right subtrees + 1 
	}
}

The basic set of operations is as follows:

//lchild points to left child node, rchild points to right child node 
struct BTNode{ElemType data; BTNode *lchild; BTNode *rchild;};
//Creating Binary Trees from Bracket Expressions str 
void CreateBTree(BTNode * &b,char *str){
	BTNode *St[MaxSize],*p=NULL;//St is the stack that stores parent nodes with child nodes, top is the top of the stack, and the new node is the child node of the top of the stack node 
	int top=-1,k,j=0; char ch;//k is used to identify whether the current traversed child node is a left or a right child node, 1 left and 2 right 
	b=NULL;	ch=str[j]; 
	while (ch!='\0'){
   	   	switch(ch){//If the left half bracket indicates that the current node has a child node, put the node on the stack, the first child node must be the left child node, k=1 
		case '(':top++; St[top]=p; k=1; break; 
		case ')':top--; break;//The subtree of the top node of the stack traverses completely, leaving the stack 
		case ',':k=2; break;//A comma is encountered indicating that there is a new child node, which is the right child node, k=2 
		default:p=(BTNode *)malloc(sizeof(BTNode));//Encountered a character indicating a new node, allocating space and assigning values to the node 
				p->data=ch; p->lchild=p->rchild=NULL;
				if (b==NULL) b=p;//The first character encountered is the root node
				else{//The current node is a child of the top node of the stack, establishing a pointer from the root node to the child node	
					switch(k){//Determine whether it is a left or right child node based on k 
						case 1: St[top]->lchild=p; break;
						case 2: St[top]->rchild=p; break;
					}
				}
		}j++; ch=str[j];
	}
}//Output Binary Tree
void DispBTree(BTNode *b){
	if (b!=NULL){printf("%c",b->data);//Print Root Node 
		if (b->lchild!=NULL||b->rchild!=NULL){//Nodes with children print brackets, and subtrees with left and right recursively 
			printf("("); DispBTree(b->lchild);//Print left parenthesis, recursively print left subtree				
			if (b->rchild!=NULL) printf(",");//Output only when there is a right child node,
			DispBTree(b->rchild); printf(")");//Recursively print right subtree, print right half bracket					
		}
	}
}//Destroy Binary Tree
void DestroyBTree(BTNode *&b){
	if (b!=NULL){//First destroy the left and right subtrees, then the root node	
		DestroyBTree(b->lchild); DestroyBTree(b->rchild); free(b);
	}
}//Find Nodes
BTNode *FindNode(BTNode *b,ElemType x) {BTNode *p;
	if (b==NULL) return NULL;//b is empty, abandon search 
	else if (b->data==x) return b;//Find the root node whose value is x and return b 
	else{p=FindNode(b->lchild,x);//Find left subtree 
		if (p!=NULL) return p;//The left subtree has a node P with the value x, returning p 
		else return FindNode(b->rchild,x);//Otherwise, find the right subtree 
	}
}//Find Left Child Node 
BTNode *LchildNode(BTNode *p){return p->lchild;}
//Find Right Child Node 
BTNode *RchildNode(BTNode *p){return p->rchild;}
//Finding the Height of a Binary Tree 
int BTHeight(BTNode *b) {int lchildh,rchildh;//lchildh is the height of the left subtree and rchildh is the height of the right subtree 
	if (b==NULL) return(0);//Empty tree height returns 0
	else{//Finding the Height of Left and Right Subtrees 
		lchildh=BTHeight(b->lchild); rchildh=BTHeight(b->rchild);
		return (lchildh>rchildh)?(lchildh+1):(rchildh+1);//The current tree height is the maximum height of the left and right subtrees + 1 
	}
}

Traversal of Binary Trees

That is the four traversal methods in the previous chapter - three recursive traversals and one hierarchical traversal.

Recursive algorithm of sequential traversal followed by sequential traversal

That is, direct formulas are done recursively, with specific formula references This article.

//Recursive algorithm for sequential traversal
void PreOrder(BTNode *b){
	if (b!=NULL){//RreOrder(T)=root node of T+RreOrder(left subtree of T)+RreOrder(right subtree of T)
		printf("%c ",b->data); PreOrder(b->lchild); PreOrder(b->rchild);
	}
}//Recursive algorithm for intermediate traversal
void InOrder(BTNode *b){
	if (b!=NULL){//InOrder(T)=InOrder(left subtree of T)+root node of T+InOrder(right subtree of T)	
		InOrder(b->lchild);	printf("%c ",b->data); InOrder(b->rchild);
	}
}//Recursive algorithm for post-order traversal
void PostOrder(BTNode *b){
	if (b!=NULL){//PostOrder(T)=PostOrder(left subtree of T)+PostOrder(right subtree of T)+root node of T
		PostOrder(b->lchild); PostOrder(b->rchild); printf("%c ",b->data); 
	}
} 

Related exercises

7.11

Design an algorithm to find the number of all nodes of a binary tree.

Analysis: The number of nodes of binary tree T = the number of nodes of left subtree + the number of nodes of right subtree + 1. Just follow this recursive formula:

int Nodes(BTNode *b){
	if (b==NULL) return 0;//Number of empty tree return nodes is 0 
	else return Nodes(b->lchild)+Nodes(b->rchild)+1;//Otherwise, the number of nodes in the tree = the sum of the number of left and right subtree nodes + 1 
}

7.12

7.12 Don't do this because it doesn't tell you exactly how to output it.

7.13

Designs an algorithm to find the hierarchy (or depth) of a node whose node value is x in a binary tree.

Analysis: is the property of the depth of finding one more node currently being queried than is common.

int Level(BTNode *b,ElemType x,int h){//h is the depth of node b currently being queried with an initial value of 1	
	int l; 
	if (b==NULL) return(0);
	else if (b->data==x) return(h);//If a hierarchy is found that returns the current node 
	else{	
		l=Level(b->lchild,x,h+1);//Find in left subtree
		if (l!=0) return(l);
		else return(Level(b->rchild,x,h+1));//Not found in left subtree, then look in right subtree
	}
}

7.14

Design an algorithm to find the total number of k-level nodes in binary tree b.

Analysis: As with the above problem, when traversing to a node with a depth of k, the total number is + 1, and then down the node does not need to care about it.

int n=0;//n as global variable record 
void Lnodenum(BTNode *b,int h,int k){//h is the current depth 
	if (b==NULL) return;//Empty Tree Return 
	else{
		if (h==k) n++;//Currently accessed node at layer k, n increments 1
		else if (h<k){//Recursively find left and right subtrees if the current node level is less than k
			Lnodenum(b->lchild,h+1,k,n); Lnodenum(b->rchild,h+1,k,n);
		}//Nodes deeper than k are better without regard to them 
	}
}

7.15

·······

7.16

Designs all ancestors of a node whose output value is x.

Analysis: When querying the current node, first look at whether the value of the child node is X. Otherwise, the left and right subtrees are queried. If there are nodes with value x in the left and right subtrees, the current node is the ancestor of the node with value X.

bool ancestor(BTNode *b,ElemType x){
	if (b==NULL) return false;//Finding an empty tree has not returned a result, indicating that it has no result with a value of x and returns false 
	else if (b->lchild!=NULL&&b->lchild->data==x||b->rchild!=NULL&&b->rchild->data==x){
		printf("%c ",b->data); return true;//The value of the child node is x, indicating that the current node returns true for the required node 
	}//Finds left and right subtrees, returns true if left and right subtrees have nodes with a value of x 
	else if (ancestor(b->lchild,x)||ancestor(b->rchild,x)) {printf("%c ",b->data); return true;}
	//Neither the left nor the right subtree has a node with a value of x, indicating that there is no node with a value of X in the whole tree, returning false 
	else return false;
}

Non-recursive algorithm for sequential ordering followed by sequential traversal

Previously, recursive algorithms were designed because binary trees are a recursive data structure. The design method of binary tree non-recursive algorithm is introduced here.

Sequential traversal non-recursive algorithm

The design of non-recursive algorithms is often to use stacks to simulate the operation of function recursive stacks. In a recursive algorithm of sequential traversal, the function recursion stack first places all functions that traverse the left subnode in the function recursion stack and processes the left subnode. When there is no down left child node, the recursive stack goes out and the right child node of the node this function is working on is put in the function recursive stack. The right child node also finishes processing all the trees corresponding to the parent node representing this right child node.

The idea of converting this to a non-recursive algorithm is very good: first, the left subnode is traversed all the time, putting the node on the whole chain of the left subnode into the stack. When the chain of left child nodes is finished, consider the top element of the stack and place the right child node of the top element in the stack for processing. When the stack is empty, the entire tree is processed (an empty node represents the downward tree processing of a node; that is, it does not continue downward, it does not mean that all nodes are processed).

//Sequential non-recursive traversal algorithm
void PreOrder2(BTNode *b){//p traverses the entire binary tree, and the st stack stores nodes that handle only the left child nodes 
	BTNode *p; p=b; SqStack *st; InitStack(st);//The top element of the stack is the node that we need to process the right child node first				
	while (!StackEmpty(st)||p!=NULL){//Complete end of traversal when stack is empty 
		//All the left child nodes in the chain where the left child node is located are stacked. According to the recursive formula, the lowest node traverses the right child node first, that is, the top element of the stack. 
		while (p!=NULL){printf("%c ",p->data);//Processing Root Nodes	
			Push(st,p); p=p->lchild;			
		}//Handles the right child node of the top element of the stack 
		if (!StackEmpty(st)){Pop(st,p); p=p->rchild;}
	}printf("\n"); DestroyStack(st);//Destroy Stack
}

On the contrary, for each new traversed node, we first need to print the value of the current node, then traverse the left subnode until the left subnode is empty. In the process of the right node, the formula is also consistent: RreOrder(T)=root node of T+RreOrder(left subtree of T)+RreOrder(right subtree of T).

The above algorithm can be derived either from formula inference or from recursive stack to stack.

Medium-order traversal non-recursive algorithm

Think and code are mostly the same, because middle traversal also deals with the left subtree first, that is, putting all the left child nodes in the chain where the left child node is located on the stack. The difference is that middle traversal handles the root node in the middle, which means that the time to handle the root node needs to be before the left child node is processed and the top element earpin right child node is processed out of the stack.

//Medium-order non-recursive traversal algorithm
void InOrder2BTNode *b){//p traverses the entire binary tree, and the st stack stores nodes that handle only the left child nodes 
	BTNode *p; p=b; SqStack *st; InitStack(st);//The top element of the stack is the node that we need to process the right child node first				
	while (!StackEmpty(st)||p!=NULL){//Complete end of traversal when stack is empty 
		//All the left child nodes in the chain where the left child node is located are stacked. According to the recursive formula, the lowest node traverses the right child node first, that is, the top element of the stack. 
		while (p!=NULL){Push(st,p); p=p->lchild;}//Print the root node, then process the right child of the top element of the stack 
		if (!StackEmpty(st)){Pop(st,p); printf("%c ",p->data); p=p->rchild;}
	}printf("\n"); DestroyStack(st);//Destroy Stack
}

Post-order traversal non-recursive algorithm

It is also okay to do the same thing before traversing all the left child nodes in the chain where the entire left child node is located, and then the right child node of the top element of the stack.

The obvious problem with this is that root nodes must be processed from the bottom up, which means that when you want to process the right subtree of a higher-level node, most of its nodes must have been processed completely, and reprocessing them all will waste a lot of time.

When we stack all the left child nodes, we process the right child node of the top element of the stack. If the last processed node is the right child of the current top node of the stack, then both left and right child nodes are processed, and the nodes below the top node of the stack need not be processed further down. If not, then the last processed node must be the left child of the top element of the stack, which means the right subtree has not been processed yet. A full traversal of the right subnode (right subtree) is required.

//Post-order non-recursive traversal algorithm
void PostOrder(BTNode *b){//p traverses the whole tree, r is used to save the last processed node 
	BTNode *p,*r; p=b; SqStack *st; InitStack(st); bool flag;//flag indicates whether or not the top node of the stack is being processed 
	do{//Traverse all the left child nodes in the chain where the whole left child node is located first
		while (p!=NULL){Push(st,p);	p=p->lchild;}
		r=NULL;	flag=true;//r Initial value is empty every time from bottom to top					
		while (!StackEmpty(st)&&flag){GetTop(st,p);
			//P->rchild==r, that is, the last processed node is determined to be the right child node of the current top node of the stack, the right child node is processed, and the left child node is definitely processed			
			if (p->rchild==r){printf("%c ",p->data);//Processing Root Nodes 
				Pop(st,p); r=p;//r Stores the most recently processed nodes
			}//Otherwise, the last processed node is the left sub-node of the top node of the current stack, the right sub-tree reaches bah, r is empty, and the right sub-tree is reprocessed 
			else{p=p->rchild; flag=false;}
		}
	}while (!StackEmpty(st));		
	printf("\n"); DestroyStack(st);//Destroy Stack
}

7.17

Designing an algorithm to output an inverse sequence of paths from the root node to each leaf node requires a posterior non-recursive traversal algorithm.

Analysis: Based on the characteristics of subsequent non-recursive algorithms, the path from the root node to each leaf node is the node stored in the stack when traversing to a leaf node. Simply change the part of the printed leaf node to all the values in the output stack.

Code is not duplicated.

Hierarchical traversal algorithm

Hierarchical traversal starts from the root node and accesses each node in the tree in top-down, left-to-right order. This traversal method is very intuitive to people. However, for machines, since there is no connection between nodes of the same layer, the key is how to traverse the nodes of the same layer from left to right in order.

Let's assume that we now have a left-to-right hierarchical traversal sequence of the kth level, and need a left-to-right hierarchical traversal sequence of the next level. The easiest way is to traverse the kth level sequence from left to right, and then get the left and right sub-nodes of the query node each time, since the left sub-node must be on the left of the right sub-node. The right child of the k-level ith node must also be to the left of the left child of the i+1 node. So you know that accessing child nodes through a left-to-right query of the k-level hierarchical traversal sequence is bound to result in the next-level hierarchical traversal sequence. And the combination of the sequence traversal sequence of all layers is the complete sequence.

Essentially, it transfers the order between the preceding nodes to the newly added nodes.

Since we only need to query the last node of the hierarchical traversal and the query node from the back, queues can generally satisfy this requirement:

void LevelOrder(BTNode *b){BTNode *p; SqQueue *qu; InitQueue(qu); enQueue(qu,b);//Root Pointer Queue
	while (!QueueEmpty(qu)){deQueue(qu,p);//Query the queued nodes in turn from left to right for each query 
		printf("%c ",p->data);//Print Query Nodes 
		//Query the child nodes, first bring the left child nodes into the queue, then the right child nodes into the queue, so that the order of the previous layer from left to right is transferred to the next layer 
		if (p->lchild!=NULL) enQueue(qu,p->lchild); if (p->rchild!=NULL) enQueue(qu,p->rchild);
	} 
}

Construction of Binary Trees

Simply put, a unique binary tree can be constructed from either the middle and the first or the last sequence of a binary tree traversal sequence.

Make a concise statement:

Mathematical induction using the number of nodes n of a binary tree, when n=0, the result is obviously valid.

We assume that the conclusion holds true for n<k. When n=k, we can assume that the result of median order traversal is a1a2 ak, and that of sequential or sequential traversal is b1b2 Bk. Based on the rules of sequential traversal and sequential traversal (first traversing the root node or last traversing the root node), we can determine that their root is c(c=b1 or bk). Then, according to the value of the node, we can query ar=c in the sequential traversal sequence a1a2 /. ak. In this way, we can divide the middle traversal sequence into the middle traversal sequence of the left subtree of a1a2 a R and the middle traversal sequence of the right subtree of a(r+1)a(r+2) ak. At the same time, based on the number of nodes of two subtrees, we can also infer the sequence of first and second order traversal of left and right subtrees in b1b2.

At this time, we get the sequence of the left and right subtrees in order of traversal and the sequence of the left and right subtrees in order of traversal respectively. The number of nodes of the left and right subtrees must be less than k. A binary tree can be constructed by mathematical induction. Binary trees and root nodes of left and right subtrees can construct a complete binary tree, which is proved.

The code is as follows:

//Preis the first element of the sequential traversal sequence, in is the first element of the sequential traversal sequence, n is the current number of binary tree nodes, and p stores the location of the root node in the sequential traversal sequence 
BTNode *CreateBT1(char *pre,char *in,int n){BTNode *s; char *p; int k;//k is the root node in the middle traversal position, also the number of left subtree nodes 
	if (n<=0) return NULL;//n Less than or equal to 0 means an empty tree 
	s=(BTNode *)malloc(sizeof(BTNode));	s->data=*pre;//The first node of the sequential traversal sequence is the root node s 
	for (p=in;p<in+n;p++) if (*p==*pre) break;//Find Root Node in Ordered Traverse							
	k=p-in;//Determine Root Node 
	s->lchild=CreateBT1(pre+1,in,k);//Recursively Construct Left Subtree 
	s->rchild=CreateBT1(pre+k+1,p+1,n-k-1);//Recursively Construct Right Subtree
	return s;
}//post is the first element of the sequential traversal sequence, in is the first element of the sequential traversal sequence, n is the current number of binary tree nodes, and p stores the location of the root node in the sequential traversal sequence 
BTNode *CreateBT2(char *post,char *in,int n){BTNode *s; char r,*p; int k;//k is the root node in the middle traversal position, also the number of left subtree nodes
	if (n<=0) return NULL;//n Less than or equal to 0 means an empty tree
	r=*(post+n-1); s=(BTNode *)malloc(sizeof(BTNode)); s->data=r;//The last node of the post-order traversal sequence is the root node s
	for (p=in;p<in+n;p++) if (*p==r) break;//Find Root Node in Ordered Traverse
	k=p-in;//Determine Root Node							
	s->lchild=CreateBT2(post,in,k);	//Recursively Construct Left Subtree
	s->rchild=CreateBT2(post+k,p+1,n-k-1);	//Recursively Construct Right Subtree
	return s;
}

7.19

Design an algorithm to convert the sequential storage structure of a binary tree into a chain storage structure.

Analysis: Sequential storage structure itself is not the focus of binary tree storage structure, which is not discussed here.